黑白棋盘网格中的交互式直线检测
李晓芳
(山西工商学院 计算机信息工程学院, 山西 太原 030000)
0 引 言
黑白棋盘网格是摄像机标定[1-4]中常用的空间标定模板,经典的摄像机标定方法是通过空间标定模板特征与图像特征之间的对应关系来构建关于摄像机模型参数的约束条件,然后通过优化算法求解摄像机的内外参数。直线作为棋盘网格图像的重要特征,其检测精度的高低直接影响到摄像机内外参数的精度。因此,研究黑白棋盘网格图像的直线检测对摄像机标定具有很重要的意义。
目前,相关研究大都是基于Hough[5-7]变换的,如宋雪峰等[8]通过引入边缘提取、Hough变换、灭点检测等图像处理技术,对网格状地面图像进行了垂直和水平两个方向的直线检测;肖晓明等[9]在Laplacian算子和Hough变换的基础上进行改进,提出一种适用于背景相对简单的网格图像直线检测方法等。但是Hough变换直线检测方法对参数选取非常敏感,参数选取对最终的检测精度有重要影响。针对这些问题,文中结合黑白棋盘网格图像的特点,围绕黑白棋盘网格图像直线检测问题进行研究,并给出一种切实可行的方法。
利用棋盘网格已知的结构尺寸,给出一种基于平面单应矩阵的直线检测方法,并开发了一个人机交互棋盘网格直线检测系统。该系统只需在图像中手动选取四个角点,然后系统利用模板点和图像点的对应关系求出平面间的单应矩阵,并自动检测出图像中的直线特征。该方法检测速度快,鲁棒性高,且具有较高的检测精度,实验结果也验证了该方法的可行性,而且该方法也很容易扩展到其它复杂的平面图像直线检测问题中。
1 基础知识
1.1 线性最小二乘法
已知一组点的坐标为(xi,yi),其中i=1,2,…,m。在平面内,可用下列方程唯一确定一条直线,
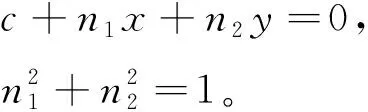
(1)
单位向量(n1,n2)垂直于式(1)中的直线。如果p点在该条直线上,则该点坐标(xp,yp)满足式(1),即
c+n1xp+n2yp=0,
若p点在直线外,则可计算
r=c+n1xp+n2yp,
(2)
|r|即为p点到直线的距离。
通过这些直线拟合一条直线,则只需满足
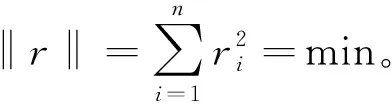
(3)
求解
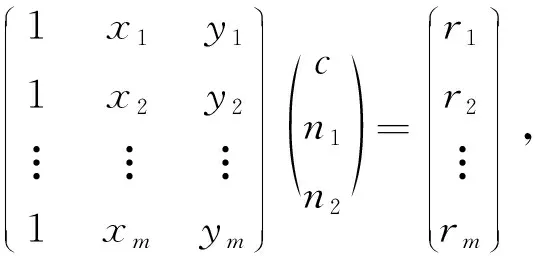
(4)
得出直线参数c,n1,n2,即可得出拟合直线的方程。
1.2 二维射影几何[10]
1.2.1 点和线的齐次表示
二维空间(即平面)中直线方程的一般形式为
ax+by+c=0,
a,b,c可以任意取值,且当取值不同时所表示的直线也不同,则二维空间中的任意一条直线可以直接用对应的矢量(a,b,c)T表示。此外,直线和矢量(a,b,c)T并不是一一对应的关系。因为,对于任意的非零常数k,方程
ax+by+c=0
和
k(ax+by+c)=(ka)x+(kb)+y(kc)=0
是等价的,代表同一条直线。为此,矢量(a,b,c)T和k(a,b,c)T为相同的直线,则用矢量(a,b,c)T作为该类直线的齐次矢量,记作l=(a,b,c)T。注意矢量(0,0,0)T不代表任何直线。
方程ax+by+c=0也表示点x=(x,y)在直线l=(a,b,c)T上,矢量内积的形式为
ax+by+c=(x,y,1)(a,b,c)T=
(x,y,1)l=0,
即在二维欧式空间R2中的点(x,y)T的基础上增加一个分量1,使其变为三维矢量。对于任意的非零常数k,矢量(x,y,1)T和(kx,ky,k)T是等价的。同理,矢量(x,y,1)T为该类点(x,y)T的齐次表示。注意矢量(x,y,0)T表示二维射影空间(平面)中的无穷远点。
1.2.2 射影映射
定义1射影映射是二维射影空间P2到它自身的一种满足下列条件的可逆映射h:三点x1,x2,x3共线当且仅当h(x1),h(x2),h(x3)也共线。
定理1映射h:P2→P2是射影映射的充分必要条件,是存在3×3的非奇异矩阵H,使得二维射影空间P2中的任意一点x都满足h(x)=Hx。
1.2.3 射影变换
定义2平面射影变换可用一个非奇异3×3矩阵H表示为
或
x′=Hx。
(5)
其实质是一种线性变换。其中,矩阵
被称为射影矩阵或单应矩阵。
注意,此方程中的矩阵H是一个齐次矩阵,即在相差一个比例因子的情况下式(5)中的等号才成立。严格地,式(5)应写为
λx′=Hx,
式中:λ----比例因子。
中心投影把一张平面的点映射成另一张平面上的点和把一张平面上的直线映射成另一张平面上的直线,如图1所示。
从图1可知,沿一个公共点(投影中心)的射线的投影定义了从一张平面π到另一张平面π′的映射。
射线模型中(见图1),一个射影变换就是三维欧氏空间R3中的一种线性变换,在变换过程中保持所有的射影性质不变。从定义1可知,在透视图形中,中心投影将一张平面上的点映射为另一张平面的点。同样,中心投影将一张平面上的直线映射为另一张平面上的直线,且直线之间的变换为
I′=H-Tl。
(6)
1.3 Harris角点检测
角点检测(Corner Detection)是计算机视觉系统中用来获取图像特征点的一种方法,也称为特征点检测。角点没有明确的数学定义,通常角点是两条或两条以上边缘的交点。Harris角点检测算子是由Chris Harris等[11]提出的,他们利用Taylor展开方法将偏移的方向进行了任意方向的扩展,同时引入了高斯平滑函数,用以增加抗噪声干扰的性能。他们在图像中设计了一个局部移动的窗口,窗口在各个方向没有明显灰度变化的为平滑区域,只在某个方向没有灰度变化的为边缘,在任意方向都导致图像灰度明显变化的即为角点。他们用微分算子替代了亮度块的方向移动,并用自相关函数构造了2×2的Harris矩阵。用来判断图像特征是哪种特征的矩阵M公式
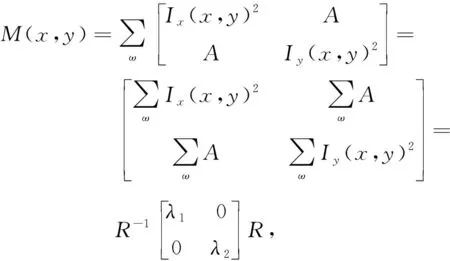
(7)
式中:A=Ix(x,y)Iy(x,y)。
将矩阵对角化处理,得到两个正交方向的变化量分量,对角线元素即为矩阵的特征值λ1,λ2,具体有如下三种情况。
1)直线:λ1≫λ2或λ2≫λ1。
2)平面:λ1≅λ2,且λ1,λ2均较小。
3)角点:λ1≅λ2,且λ1,λ2均较大。
R值与点的类型关系如图2所示。
Harris算法具有旋转不变性、稳定性高、对噪声不敏感等优点,则在信噪比较低的图像中仍然可以比较准确地检测出图像中的角点。
2 基于最小二乘的交互式直线检测方法
2.1 基本原理法
2.1.1 直线检测基本原理
该直线检测方法直接利用了射影变换保持点线关系不变性,及两个平面π和π′之间的射影矩阵H不变。通过手动获取四个角点(四个角点为同一个矩形的四个顶点),求出初始的直线位置,再利用最小二乘法将同一条直线附近的边缘点拟合出精度更高的直线参数。
2.1.2 直角坐标系的建立
假设世界平面为模板平面π,拍摄的图片为图像平面π′,并分别在模板平面和图像平面的左上角建立直角坐标系O-xy和O-x′y′,如图3所示。
2.1.3 射影矩阵H的计算
通过前面的二维射影变换的基础知识及分析可得,射影矩阵H,即3×3的非奇异矩阵,同时也是齐次矩阵,类似于点的齐次坐标。在二维射影矩阵H中,有意义的只是元素的比率,则其九个元素中有八个独立比率,即有八个独立自由度。从式(4)、式(5)可知,两个平面之间的每对对应点提供两个限制条件,那么这两个平面间的四对对应点(任意三点不共线)即可唯一确定一个射影矩阵H。
利用棋盘网格的特点可求出模板平面π中的所有角点的齐次坐标
xi=(xi,yi,1)T,
再利用Harris角点检测算子可以检测出图像平面π′中感兴趣区域内的所有角点,并得到角点坐标
将其中一对点的齐次坐标代入式(5),可得
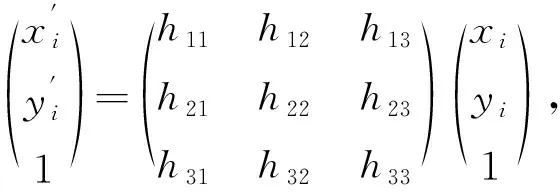
(8)
将上式展开得:

(10)
1=h31xi+h32yi+h33,
(11)
式(9)和式(10)分别除以式(11),得:
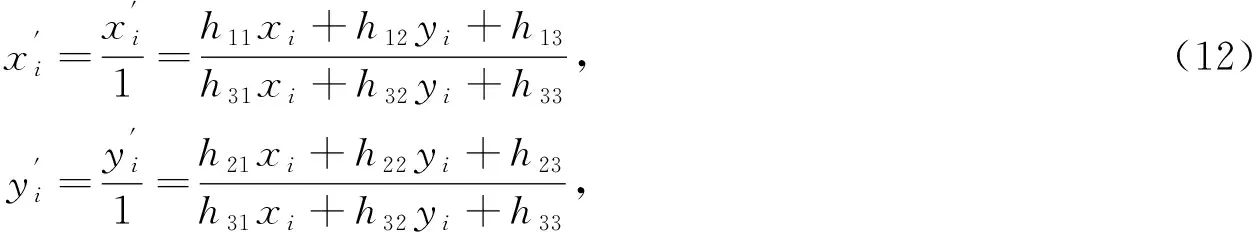
(13)
继续化简式(12)和式(13),得:
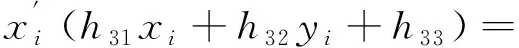
h11xi+h12yi+h13,
(14)
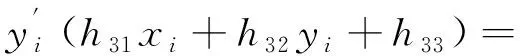
h21xi+h22yi+h23。
(15)
对于图像平面π′和世界平面π的任意一对对应点都满足式(14)和式(15),将四对对应点(其中任意三对对应点不共线)均代入式(5),令h33=1,化简整理得
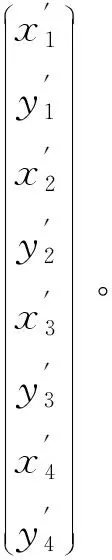
(16)
因为任意三对对应点都不共线,则式(16)的8×8矩阵为非奇异矩阵,即满秩矩阵,所以可以直接求解方程,从而解得射影矩阵H中的各个元素。
2.1.4 直线之间的射影变换矩阵
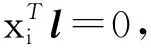
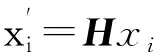
l′=H-Tl,
也可以写为
l′T=lTH-1。
结合黑白棋盘网格的特点,即可求出模板平面π中的所有直线的齐次表示
li=(ai,bi,ci)T,
再利用直线与直线之间的射影变换关系式l′=H-Tl及求得的射影矩阵H,即可求出图像平面π′中感兴趣区域的所有直线的齐次表示
li=(ai,bi,ci)T。
2.2 算法步骤
基于以上分析,直线检测算法流程如图4所示。
具体步骤如下:
1)读入图像I(x,y);
2)选取感兴趣区域。为了降低黑白棋盘网格模板外像素点的影响,可以采取线性规划的方法选取模板区域,得到图像I1(x,y),若为彩色图像转化为灰度图像I2(x,y);
3)利用Canny算子对图像I2(x,y)进行边缘检测,得到图像I3(x,y);
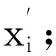
5)实际黑白棋盘网格上,标记其左上角的某个角点,作为坐标系原点O,并建立直角坐标系O-xy,再根据模板中相邻平行直线的实际间距,计算角点坐标xi及直线方程li;
6)在感兴趣区域按逆时针手动点四个点(四个点必须为同一个矩形的四个顶点),利用点与点之间的射影变换关系式x′=Hx,求得实际模板平面和图像平面I(x,y)之间的射影变换矩阵H;
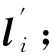
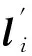
9)在原图像I(x,y)上绘制原有的直线。
2.3 实验结果分析
为了得到理想的实验结果,先利用型号为Nikon D300s的摄像机和方格边长分别为30、40、50 mm的黑白棋盘网格模板,采集不同距离(摄像机离模板的距离不同)、不同倾斜度、不同旋转度和方格尺寸大小不同的分辨率为2 144×1 424 pixel的图像,然后在MTLAB R2008a平台下进行大量实验,最后从参数选取的角度将该方法与传统Hough变换直线检测方法进行比较。
2.3.1 实验结果
具有代表性的不同距离、不同倾斜度、不同旋转度和方格尺寸大小不同的黑白棋盘网格图像如图5所示。
图5四幅图片的直线检测结果如图6所示。
图中所显示的大方框区域表示感兴趣区域,十字表示检测出的角点,直线表示检测出的直线。
2.3.2 结果分析
以图5(a)进行实验分析,为了更清晰地观察实验结果,文中只附模板区域的放大图片。
从图6可知,对于棋盘网格图像来说,文中基于二维射影变换的直线检测方法不仅有较快的检测速度,而且用肉眼看,检测精度也比较高。因为图像平面上的一条直线仅与模板平面的一条直线对应,所以检测过程中不会出现重线、误检和漏检现象。
传统Hough变换方法和基于二维射影变换的直线检测结果如图7所示。
从参数选取角度来说,该方法的参数明显比传统Hough变换方法的参数选择容易。该直线检测方法的参数包含感兴趣区域模板水平方向的方格个数Nx和竖直方向的方格个数Ny及模板的方格边长n(mm)。只要模板和感兴趣区域确定了,那么这三个参数即可确定,并且参数的确定不会影响到直线检测精度,更不会导致误检、漏检、重线等现象。而Hough变换参数dρ和dθ的选取相当敏感,并且参数的选取不当会导致误检、漏检和重线等现象。
3 结 语
采用已知结构尺寸的黑白棋盘网格图像,给出一种基于平面单应矩阵的直线检测方法,并开发了一个人机交互棋盘网格直线检测系统。该系统只需在图像中手动选取四个角点,然后系统利用模板点和图像点的对应关系求出平面间的单应矩阵,并自动检测出图像中的直线特征。该方法检测速度快,鲁棒性高,且具有较高的检测精度,实验结果也验证其可行性,而且也很容易扩展到其它复杂的平面图像直线检测问题中。

