木材干燥质量的概率神经网络预测

韩维娜， 张秀梅

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

0 引 言

随着木材加工业的深入发展，木材干燥后的质量决定了其商品的使用价值[1]。木材干燥过程的优化基于三个主要标准：干燥时间、能耗和木材的质量[2-3]。干燥过程中木材的变形直接关系到干燥木材的质量，从而影响经济效益[4]。此外，控制干燥木材的最终含水量(Moisture Content, MC)在优化木材干燥过程中发挥着重要作用，因为过度干燥会导致木材形变增加、能耗增加和窑生产率降低，而欠干燥会导致木材不符合最终含水率的等级要求[5]。

人工神经网络(ANN)是由高度互联的神经计算元件组成的网络，具有响应输入刺激和学习适应环境的能力[6-7]。人工神经网络提供了一个有用和有效的工具对自然界中出现的复杂和不被理解的过程进行建模[8]。因为它们能够从数据中提取模型输入和输出之间的权值关系，而无需明确考虑实际的数据生成过程。关于人工神经网络模型在木材干燥中的应用较少。Avramidis等[9]通过人工神经网络预测了木材干燥窑的干燥速率，利用初始含水量、基本密度和干燥时间三个输入预测最终木材的平均含水率，实验结果验证了预测值的准确性。

虽然有一些关于使用人工神经网络估计木材含水率的研究，但是并没有关于人工神经网络预测干燥木材等级的论文[10-11]。由于能源成本增加和对盈利的关注，文中旨在建立一个人工神经网络模型来预测木材等级，根据干燥窑中初始木材含水率、密度、翘曲的数据进行木材等级预测[12-14]。

1 材料和方法

落叶松木材从黑龙江省某家锯木厂获得，规格为5 cm(厚)×10 cm(宽)×300 cm(长)。为减少运输过程中的水分损失，将样本分块堆放，在黑龙江省哈尔滨市进行了干燥试验。从原始300 cm长的木材每端切下5 cm的截面，通过烘箱干燥法测定初始含水量。木材的单个经度(弯曲、翘曲和扭曲)用金属台和锥度规手工测定。此外，还测定了烘干前后的单个样品重量。实验用干燥窑容积为20 m3，热量由一个电加热器线圈(52 kW)提供，蒸汽由预设压力0.1 MPa的锅炉提供。目标含水率预设为15%，木材烘干至平均15%后，停止烘干。干燥后，手动评估单个木材经度。

木材经度表现为弯曲、翘曲和扭曲。为了研究干燥操作对木材尺寸稳定性的影响，可通过以下方式对木材经度进行量化

木材经度=弯曲+翘曲+扭曲。

在两个不同的时间进行木材经度测量：

1)木材经度1在干燥前测定(初始)；

2)木材经度2在干燥后立即测定。

1987年NLGA标准分级规则见表1。

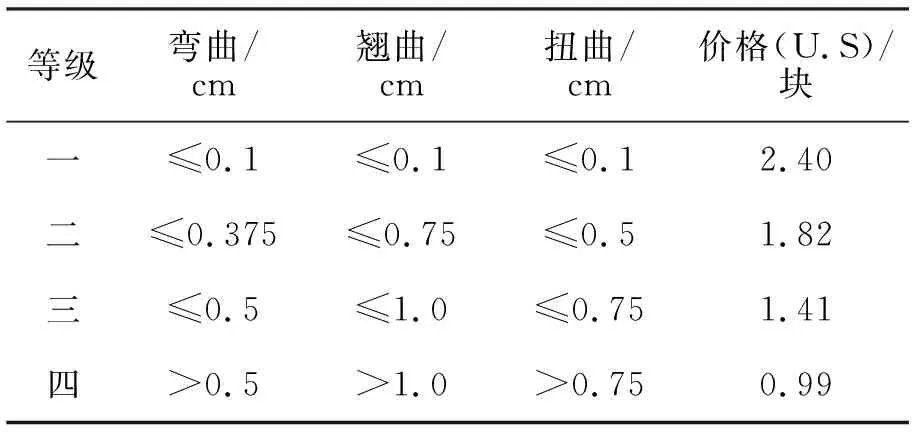
表1 板级评测标准

根据表1规则和特定等级允许的变形量，估计因干燥而产生的质量降低。

2 概率神经网络

概率神经网络是RBF网络的一个分支，是一种前馈网络,也是一个受监控的网络分类器。基于概率统计思想，由贝叶斯分类规则组成。采用Parzen函数密度估计方法对条件概率进行估计，并对模式识别进行分类。

概率神经网络的理论基础是贝叶斯最小风险准则，即贝叶斯决策理论。为分析过程简单起见，假设分类问题为二分类:c=c1或c=c2。先验概率为

h1=p(c1),

h2=p(c2),

(1)

h1+h2=1，

给定输入向量

x=[x1,x2,…,xN],

为得到的一组观测结果，进行分类的依据为

(2)

p(type1|x)为x发生情况下，类别type1的后验概率。

根据贝叶斯公式，后验概率

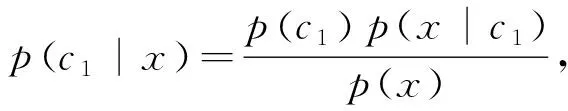
(3)

分类决策时，应将输入向量分到后验概率较大的那个类别中。实际应用中,往往还需要考虑损失与风险，将c1类的样本错分为c2类，和将c2类的样本错分为c1类所引起的损失往往相差很大，因此需要调整分类规则。定义动作αi为将输入向量指派到ci的动作，λij为输入向量属于cj时采取动作αi所造成的损失，则采取动作αi的期望风险为

(4)

假定分类正确的损失为零，将输入归为c1类的期望风险为

R(c1|x)=λ12p(c2|x),

(5)

则贝叶斯判定规则变成

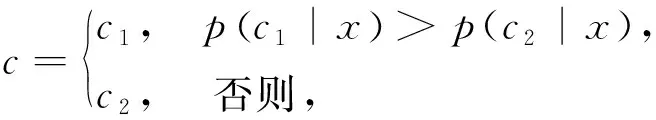
(6)

写成概率密度函数的形式，有

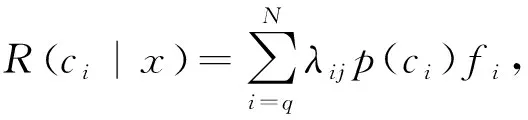
(7)

c=ci,

i=argmin(R(ci|x),

(8)

式中：fi----类别ci的概率密度函数。

PNN结构模型如图1所示。

图1分为四层：输入层、样本层(也称为模式层)、求和层和决策层(也称为竞争层、输出层)。

第一层为输入层，用于接收来自训练样本的值，将数据传递给隐含层，神经元个数与输入向量长度相等。

第二层隐含层是径向基层，每一个隐含层的神经元节点拥有一个中心，该层接收输入层的样本输入，计算输入向量与中心的距离，最后返回一个标量值，神经元个数与输入训练样本个数相同。向量x输入到隐含层，隐含层中第i类模式的第j神经元所确定的输入/输出关系由下式定义

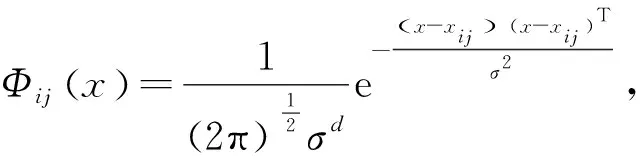
(9)

i=1,2,…,M，

式中：M----训练样本中的总类数;

d----样本空间数据的维数;

xij----第i类样本的第j个中心。

求和层把隐含层中属于同一类的隐含神经元的输出做加权平均

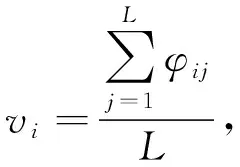
(10)

式中：vi----第i类类别的输出；

L----第i类的神经元个数。

求和层的神经元个数与类别数M相同。输出层取求和层中最大的一个作为输出类别

y=argmin(vi)。

(11)

在实际计算中，输入层的向量先与加权系数相乘，再输入到径向基函数中进行计算

Zi=xωi,

(12)

假定x和ω均已标准化成单位长度，然后对结果进行径向基运算

这相当于

(13)

式中：σ----平滑因子，对网络性能起着至关重要的作用。

层内各节点为RBF的中心，特征函数为径向基函数----高斯函数，计算了未知模式与标准模式的相似性。

将初始含水率、初始曲率、初始密度作为神经网络的输入特征向量，将四种木材板级作为输出特征向量。采用 Matlab 对基于PNN 的窑后木材质量模型进行仿真整体设计,PNN模拟训练流程如图 2 所示。

神经网络的结构和Matlab库中函数有如下对应：

第一层是输入层，属于径向基层，该层使用函数netprod计算。

第二层是模式层，是一种竞争模式的网络层，由dotprod函数来计算其所占的权重。

模型当中使用函数netsum 计算网络输入。只有newpnn的第一层才具有阈值向量，在设置的时候把第一层设置为输入向量的转置p′，并设置阈值向量为spread。在 Matlab仿真环境中可以直接通过newpnn( ) 来调用pnn 模块。第二层权值向量为目标向量T。PNN 是一种径向基网络，并且适用于模式分类领域，在设置分类时，其 spread 接近于0时构成最近的邻近分类器，当spread 值较大时,可以形成对多个训练样本的邻近分类器。然后输出，与其他方法相比，PNN可以在不进行充分计算的情况下收敛到贝叶斯最优解。

利用Matlab神经网络工具箱对模型进行配置。将数据随机分为两组，训练组数据占75%，测试组数据占25%。在整个原始数据中，这些集被作为等间距点选取。训练过程是通过比较网络输出和给定数据来进行,为了使输出值和文中使用的数据之间的误差最小化，对权重和偏差进行调整。与传统回归分析相比，神经网络方法的主要优点是不存在线性假设，具有较大的自由度，在处理非线性函数形式方面更为有效。

3 实验结果与分析

分别进行6组不同条件的干燥实验，研究了4种不同的干燥方法，其中对照1(保守)、对照2(加速)、高温干燥1(104 ℃)和高温干燥2(110 ℃)。在高温干燥1和高温干燥2实验中，进行两次干燥运行，一次用蒸汽加湿，另一次不用蒸汽加湿。

通过实验测定数据，取木材进入干燥窑时的含水率、密度和形变(弯曲、翘曲和扭曲，选择弯曲)。每个干燥窑有154个板材，即154组数据。其中10组板材数据见表2。

从154组数据中，随机选取114组数据作为训练组，40组数据作为试验组。建立了基于实验数据的PNN神经网络预测模型。表2中，将前3组数据作为输入，最后一组干燥后的木板等级作为输出数据。

表2 神经网络预测含水量的数据集

从每个干燥窑中随机抽取40组数据，将6个干燥窑数据放在一起共计240组，组成240*4的矩阵。将干燥窑含水率、密度、弯曲度作为输入，随机选取180组数据作为模型训练集，60组数据作为模型测试集。通过PNN神经网络进行预测，训练集的实际木材等级和预测木材等级如图3所示。

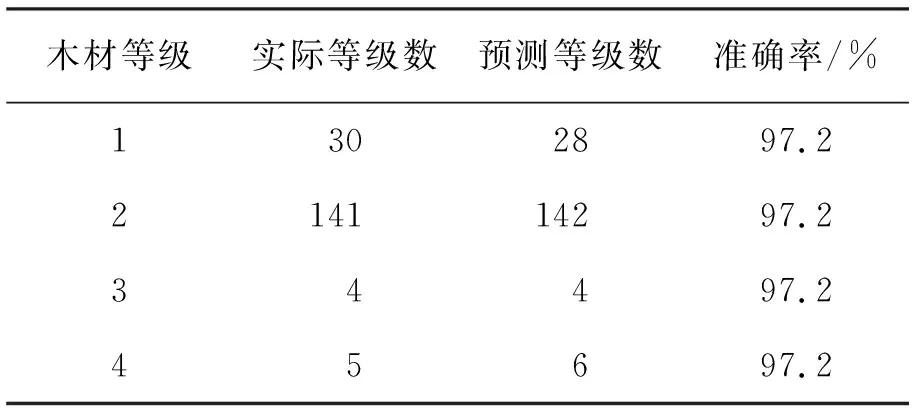
表3 PNN训练的效果与准确率

图3中三角形为训练集的实际板级，正方形为神经网络预测的训练集的输出。PNN 训练后的误差图如图4所示。

图中，纵坐标1是板级1预测错误，纵坐标0是板级正确的预测，纵坐标-1是板级2预测错误，纵坐标-2是板级4预测错误。可以看出，PNN同样适用于大数据预测。预测结果表明，该神经网络能较好地预测木材板级，具有较高的准确率。PNN可以利用线性学习算法完成非线性学习算法之前的工作，同时保持非线性算法的高精度。

6组干燥窑的预测结果如图5所示。

从图5可以看出，三角形跟正方形基本重合，说明神经网络预测的木材板级准确度较高。同时，PNN预测6个干燥窑的干燥结果没有明显差异，说明神经网络预测方法对不同的干燥方法都适用。可以看到，在干燥窑的第四和第五小组预测的数据中，只有一二级的木板，原因是该干燥窑中三四级木板较少或没有，随机选取未能选择到。

6个烘干窑的预测值和百分误差见表4。

表4 PNN预测效果和准确率

从表4可以看出，使用PNN模型进行性能预测，误差百分比较低。6个烘干窑的预测精度在95.00%以上。也就是说，不同的干燥过程对PNN板层的预测精度影响不大。

4 结 语

设计一种不需要综合实验的木材干燥后质量预测人工神经网络模型。可以根据木材进入干燥窑时的含水率、密度和形变，确定干燥处理后木材的质量。为验证该模型的有效性进行了实验研究。首先，将木材种类定位落叶松，在其进入干燥窑前，先测定材料的含水率、密度和形变，然后在进干燥窑干燥后，手动评估单个木材经度，确定木材的板级；其次介绍了利用PNN预测木材板级的流程。最后进行6组不同条件的干燥实验，对PNN预测木材板级结果和实际上手动评估的木材板级进行了对比，不同条件下，PNN预测结果均达到95.00%以上，说明设计的预测人工神经网络模型可以很好地应用到各种情况。