二维BCN的新结构及光电性质的第一性原理研究

濮春英，李春萍，吕林霞，周大伟，唐 鑫

(1.南阳师范学院 物理与电子工程学院，河南 南阳 473061；2.中国人民解放军空军航空大学 基础部，吉林 长春 130022； 3.桂林理工大学 材料科学与工程学院，广西 桂林 541004)

1 引 言

自2004年Novoselov等成功地将石墨烯剥离出来，二维材料因其优异的电学、光学及力学等性能在纳米材料中受到大量研究者的关注[1-2]。然而，石墨烯虽然具有良好的力学和导热性能及高达105的电子迁移率，但是带隙为零，导带和价带相交在同一个点，限制了它在半导体器件上的应用。因此，具有带隙的二维半导体材料成为研究者重点关注的问题。一系列具有带隙的二维材料包括过渡族二硫化物[3]、六角氮化硼[4]、过渡族碳(氮)化物[5-6]、磷烯[7-9]等均在实验上相继被合成出来。作为五族单质元素磷形成的单层磷烯因较高的载流子迁移率和带隙可调控等特点使得磷烯在光电领域具有重要的应用价值[10]，但是结构易氧化的缺点限制了它在半导体领域的应用。而作为过渡族二硫化物的典型代表，MoS2是禁带宽度为1.8 eV 的直接带隙半导体材料，在已知二维半导体中光电性能最为优越，但是载流子迁移率较低，同样限制了它在电子领域的应用。

C的两个最近邻元素B和N，形成与石墨烯类似的六角氮化硼(h_BN)二维材料[4]。但是六角氮化硼的带隙达到了～6.0 eV,为透明绝缘材料。因此，如果在二维蜂窝状结构中同时包含B、C、N这3种元素，就可以实现性质的互补，既可以弥补石墨烯零带隙的缺陷，又可以通过调节组分比实现不同带隙值的特点，从而应用在各种光电器件中。然而，实验和理论研究[11-13]均发现，由于C—C键和B—N键的键能高于C—N键和B—C键，导致实验中合成的BCN结构出现了一些富C区域和BN区域，致使B、C、N分布不均匀，出现局域的石墨烯和h_BN结构，产生相分离现象，限制了带隙的调节。Beniwal等[13]在实验上合成了化学计量比并且B、C、N均匀分布的类石墨烯结构g-BCN, 但是B、C、N原子排列仍旧未知。理论上，Zhu[14]、Azevedo[15]、Raidongia[16]等分别提出了BCN-α、BCN-γ和BCN-θ结构, Zhang等[17]采用结构搜索的方法对相同原子比例的BCN、B4C4N4和B8C8N8等进行结构搜索和能量优化，发现了BCN-β、BCN-δ、BCN-ε和 BCN-η结构，并对结构进行了详细的光电性质研究，但是对等原子比例的B6C6N6结构尚未研究。

本文利用结构搜索程序CALYSPO采用全局搜索和优化的方法对B6C6N6进行结构搜索，发现了一种新的B、C、N排列的二维BCN结构，并对其结构稳定性、电子结构、载流子迁移率、光学性质等做了详细的研究和讨论。

2 计算方法

二维BCN结构预测采用的是吉林大学马琰铭课题组开发的基于粒子群蜂窝算法的CALYSPO[18-19]程序，对通过随机变量产生的结构进行能量优化。结构搜索和能量计算均是在0 GPa和0 K下进行，我们采用了6倍BCN分子式(B6C6N6)进行结构搜索，共设置了30代，每代产生50个结构。结构优化和能量计算采用VASP程序[20]，电子-电子之间的交换关联能采用的是广义梯度近似(GGA)下的投影缀加波泛函(PBE)[21]。由于密度泛函对带隙的低估，我们采用混合密度泛函(HSE)方法[22]进行了修正。在具体计算过程中B的2s22p1、C的2s22p2和N的2s22p3电子作为价电子，芯电子和价电子之间采用布洛赫提出的投影缀加波(PAW)势描述[23]。由于是二维材料，我们在真空层方向设置2 nm用来减小层-层之间的作用。截断能和K点网格分别为520 eV和5×5×1。作用在整个晶体上的能量为10-5eV，原子受到的力在10-3eV以内时结构优化结束。截断能和K点经过测试后是收敛的。根据有限位移方法，我们采用PHONOPY程序计算了BCN的声子谱[24]。声子谱的计算采用3×3×1超胞，能量和原子受力收敛精度分别为10-6eV和10-3eV/atom。一定温度下的热力学稳定性采用NVT系综下的从头算分子动力学进行模拟。

3 结果与讨论

3.1 二维BCN结构和稳定性

图1(a)是搜索得到能量较低的二维BCN结构，该结构是由B—N环、B—C—N环和C元素构成的六角圆环交替排列而成的六角结构，每个原胞中包含6个B、6个C、6个N，对应的分子式为B6C6N6，空间群为P6/mmm(No.191)，晶体参数a=b=0.753 52 nm。从BCN的原子空间分布看出:6个C构成的C环与6个N连接形成C—N键，而6个N又与12个B形成B—N键，因此C六环嵌在6个N和12个B形成的环中间。C—C、C—N、B—N、B—B之间的键长分别为0.144 6，0.144 2，0.143 2，0.155 3 nm。二维BCN的化学键是决定结构稳定和原子成键的关键因素,通过计算BCN的差分电荷密度进一步分析BCN成键的特点。其中电荷密度的差定义为Δρ=ρsc-ρatom, 其中ρsc是电子经过自洽后得到的电荷密度，ρatom是B、C、N原子孤立存在时的电荷密度。图1(b)给出了二维BCN的差分电荷密度图。从图中不难看出C—C、C—N、B—N、B—B之间具有明显的共价键，且B—B之间共价性较强，C—N之间共价性较弱。

我们通过计算BCN凝聚能衡量结构的热力学稳定性，凝聚能的计算定义为Ecoh=(nEB+nEC+nEN-EBCN)/3n,EB、EC、EN和EBCN分别为每个B 原子、C原子、N原子和二维BCN单胞结构的能量。计算得到二维BCN的凝聚能为8.41 eV/atom，对比实验上合成的BCN-γ结构的凝聚能理论计算值(8.61 eV/atom)[16],说明我们预测的BCN结构是一种亚稳相结构。但是该结构凝聚能高于实验上合成的硅烯(3.98 eV/atom)和锗烯(3.26 eV/atom)[25]中每个原子凝聚能的理论值，因此，二维BCN在实验上是可能合成的。另外，通过计算二维BCN的声子谱来分析其动力学稳定性，如图1(c)所示，在整个布里渊区，声子的振动频率均大于零，说明二维BCN满足动力学稳定性条件。

图1 (a)二维BCN单层的结构图，B、C和N 原子分别用绿色、棕色和灰色球表示；(b)二维BCN的差分电荷密度，等能面值: 15 e·nm-3，金色: Δρ>0，青色: Δρ<0；(c)二维BCN单层的声子谱；(d)二维BCN单层的能带结构和投影态密度。

为了进一步评估二维BCN结构在一定温度下的热力学稳定性，我们采用从头算分子动力学(AIMD)方法计算BCN在1 200 K时能量随时间变化关系，如图2所示。能量随时间呈现一定的波动关系，但是能量的平均值几乎保持不变，并且经过8 ps后结构仍然保持完整的六角结构，说明BCN在1 200 K具有较高的热力学稳定性。

图2 BCN在1 200 K的温度下能量随时间变化关系。插图表示分子动力学模拟后BCN的结构。

3.2 二维BCN电子结构和载流子迁移率

二维BCN的能带结构和投影态密度如图1(d)所示。从能带结构图不难分析BCN为直接带隙半导体，价带顶和导带底均位于Γ点，利用PBE泛函计算得到BCN的带隙值为1.84 eV。由于密度泛函对带隙的低估，我们采用了混合密度泛函(HSE)进行修正，计算得到BCN带隙为2.60 eV。BCN结构的电子投影态密度的研究结果表明价带顶和导带底均是由B、C、N的2p轨道占据。通过进一步的分析表明价带顶有少部分B的2s电子占据，价带顶到导带底的跃迁是BCN产生吸收的主要原因。

载流子迁移率是衡量半导体材料性能的一个重要参数，为此，我们计算了二维BCN新结构的载流子迁移率，由于BCN是六角结构，我们需要将六角结构转变为矩形结构，转变后的结构如图3(a)中矩形虚线图所示。矩形晶胞的建立主要是为了研究载流子沿着“之”字方向和“扶手”方向上的迁移率。计算迁移率之前，依据晶胞的能带与晶胞在倒空间K点的能带色散关系计算载流子沿着两个方向上的有效质量，计算公式如下：

(1)

根据该公式计算得到二维BCN电子和空穴沿着“之”字边和“扶手”边方向上的有效质量分别为0.578m0(0.551m0)和0.518m0(0.493m0)，m0为电子静止时的质量。有效质量的大小是决定载流子大小的一个重要因素，一般来说有效质量越小，载流子传输得越快。

根据计算得到的有效质量，Bardeen和Shockley[26]提出了依据形变势理论计算载流子迁移率的公式[27]。表达式为：

(2)

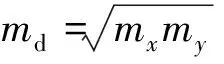
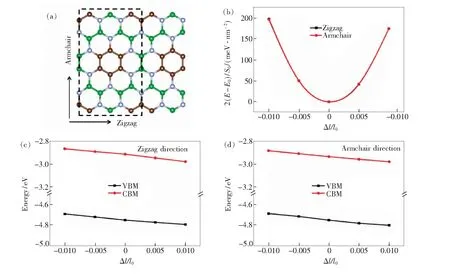
图3 (a)二维BCN单层的矩形结构图;(b)晶体能量沿着“扶手”边和“之”字边的应变关系;(c)价带顶和导带底沿着“之”字边方向的应变关系;(d)价带顶和导带底沿着“扶手”边方向的应变关系。

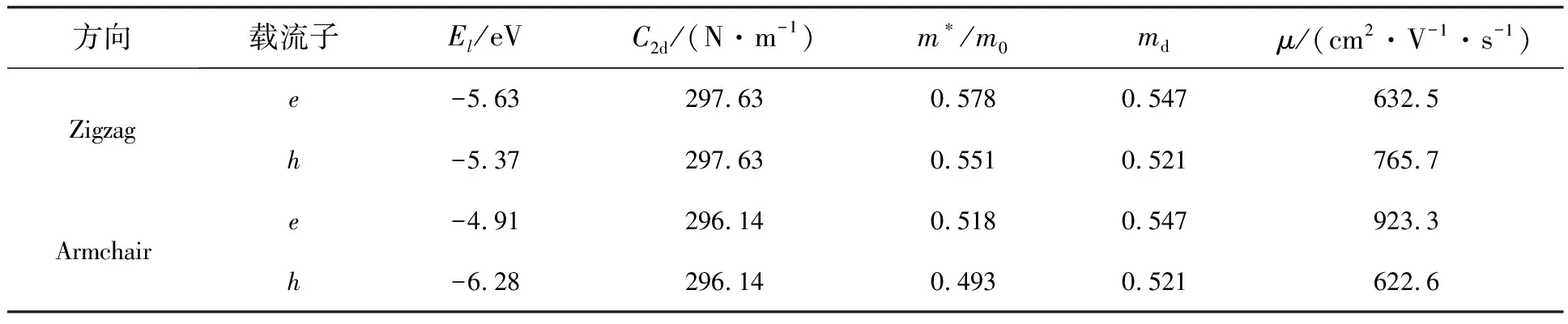
表1 二维BCN沿“之”字边和“扶手”边方向的形变势El、弹性常数C2d、有效质量m*/m0、电子e和空穴h的迁移率μ

3.3 二维BCN光学性质

介电函数反映的是材料对外加电场的影响以及电子结构在能带-能带之间转变的关系，充分反映固体能带结构和各种光谱特性。介电函数由实部εR(ω)和虚部εi(ω)构成，其中的虚部表示物质对光的吸收，实部可以通过K-K方程变换[29]得到，表示电子跃迁的共振吸收。图4(a)是计算得到的BCN的介电函数随光子能量变化关系，其中介电函数实部随光子能量增加逐渐增大，意味着介质极化程度不断增加，然后再急剧减小，BCN对电荷的束缚能力逐渐减弱。虚部曲线在～2.61，4.04，6.04，12.17 eV处出现4个主要峰值，结合能带图可以发现出现峰值时的光子能量与能带结构带隙之间存在的微小差异主要是由于电子跃迁产生的弛豫。

根据介电函数，可以获得材料的折射率、反射谱、吸收谱、光电导率和能量损失函数，其中折射率与介电函数之间的关系为εR=n2-k2，εi=2nk，公式中k为消光系数，n为折射率，根据折射率可以推断该频率下介质的透明程度。折射率和消光系数随光子能量的变化关系如图4(b)所示，光子能量在～1.77 eV时BCN出现了最大折射率为1.81，而后逐渐减小，最后稳定在0.80。图4(c)是光的反射谱，在光子能量为2.60，4.32，6.64 eV时，BCN对应的反射率分别为11.5%、10.5%和5.4%。由此可见，在可见光区域BCN最高可以反射11.5%的入射光。另外，我们对光的吸收系数进行了计算，如图4(d)所示，吸收谱的峰值对应的光子能量分别在2.89，4.25，6.34，12.34 eV位置处，与介电函数虚部的峰值相吻合。

对于反映光学性质的光电导率，可以通过介电函数的虚部得到，关系如下：σR(ω)=ε0ωεi(ω)，其中σR表示光电导的实部。图4(e)为二维半导体BCN的光电导率，Re和Im分别为光电导率的实部和虚部。根据光电导率和介电函数之间的关系不难发现光电导率的实部反映的是价带和导带之间电子跃迁的结果。因此，光电导实部峰值的位置与介电函数和吸收谱均是对应的。通过介电函数的实部和虚部可以得到BCN的能量损失函数，如图4(f)所示，BCN的最大能量损失峰位于4.80，6.94，12.57的光子能量处，对应折射率的谷值。由于B、C、N原子产生较强烈的共振，从而产生较多的能量损失。

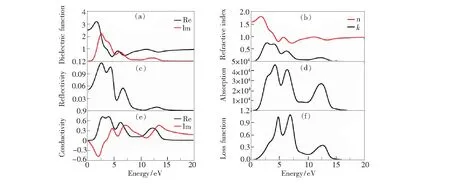
图4 二维BCN结构的介电常数(a)、折射率(b)、反射谱(c)、吸收谱(d)、电导率(e)和介电损失函数(f)。

4 结 论

通过粒子群优化算法和第一性原理计算，我们预测了一种新的B、C、N原子排列的BCN结构，该结构是由C6环、B3N3环以及B2C2N2环构成。对凝聚能声子谱的计算表明二维BCN不仅在热力学上是稳定的，在动力学上也是稳定的。通过HSE方法对能带结构的计算表明预测的二维BCN新结构是禁带宽度为2.60 eV的直接带隙半导体。根据形变势理论，我们对BCN的迁移率进行了计算，二维BCN在“之”字边和“扶手”边方向上的载流子迁移率范围为622～923 cm2·V-1·s-1。光学性质计算分析表明，BCN的介电函数虚部峰值同吸收谱和光电导率的实部峰值吻合得很好，可见光范围内的吸收峰主要集中在光子能量为～2.60 eV处，主要归因于电子从价带顶到导带底的跃迁。电学性质和光学性质的研究奠定了BCN在电子和光电子器件方面潜在的应用前景，为进一步实验提供了理论参考。