拣分条件,循路而行
姚擎宇

【摘 要】在解决数学问题时,由于题设条件的多样性、隐蔽性和复杂性,往往使得许多同学百思不解,经常找不到顺利解答的切入点,亦或是缺乏思维的连贯性,在练习或考试中寸步难行。本文通过对一道中考复习题的解答分析,谈谈关于一类解析几何问题,在处理过程中形成的经验性运用。
【关键词】长度;坐标;解析式;几何模型;切入点
一、原题呈现
在平面直角坐标系中,A点坐标(0,4),点坐标(-3,0),在直线y=x+6上找一点 P,使得△ABP构成直角三角形。求出所有满足要求的点P的坐标。
二、整体分析
本题源自中考专题复习,是典型的解析几何问题,关注数学核心素养考查。解决问题经歷观察、运算、建模等数学活动,可以抽象出一次函数、直角三角形、外接圆等基本几何图形,较好的考查了学生的构图能力。在问题解决中能引导学生在基本的图形中获取信息,融合函数、方程、相似三角形等知识,经历计算、推理等探究过程,从而考查了学生的几何逻辑推理能力和代数建模能力。
作为初中数学代数部分中不可或缺的组成部分,解析几何问题占了相当一部分比重。而学生之所以面对这类问题,常常感到无从下手,其根本原因在于不能对题设的条件进行合理归类分拣,了解它们在解题过程中不可替代的作用。
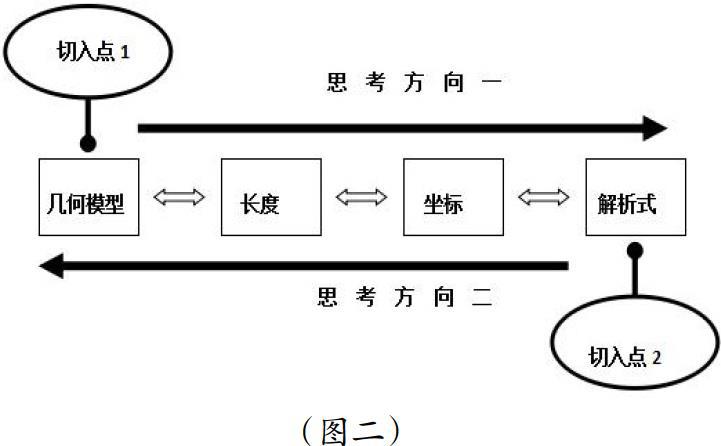
从本质上说,解析几何问题的条件设置必然包括四个基本要素,分别为:长度、坐标、解析式、几何模型。其中,长度和坐标之间可以相互转化;坐标和解析式之间具有迭代关系;几何模型又需要依靠长度关系去体现。可以发现,这四个基本要素互相依托,共同维持了整个问题的内在联系。
到此为止,我们已经把整个问题的各种情况、各种解答方法逐一整理了一遍。不难发现,对于解析几何问题,首先需要清楚地了解它们的公有条件,亦即四个基本要素:长度、坐标、解析式+几何模型。一般说来,我们往往有以下两种思路:(如图二)
方法一:用几何模型设长度→用长度写关键点坐标→将坐标代入解析式。
方法二:用解析式设点坐标→用坐标写模型内长度→用长度套几何模型。
从两种思考方向的互相比较上来说,方法一在解题思路的形成、方程的建立与解答上总是优于方法二;而方法二对于问题讨论的多种可能解的不重不漏性优于方法一。
在具体解答的过程中,需要找准合适的切入点,才能找到合适的解题捷径。大多数情况下,两种思考方向都能顺利打通从条件到结论之间的重重阻隔,但由于题设的更改、数据的限定等等因素,有时候也可能只有一种思路是可行的。这就需要我们反复思考、对比论证、发现问题、有的放矢,才能真正达到融会贯通,成竹在胸。
三、结束语
对于数学学科的解题教学,万不可满足于浅尝辄止,多思才能多解。只有知识广而深、技巧强而新、方法多而活,在遇到具体问题时才能做到随机应变、快速求解。同时,保持对题目解答的回顾思考、对比发现、总结规律、形成经验,感受了解数学解题万变不离其宗的本质内涵,必将对个人的成长大有裨益。
【参考文献】
[1]中华人民共和国教育部.数学课程标准[M].北京师范大学出版集团,2011
[2]郭思乐,喻伟.数学思维教育论[M].上海教育出版社,2007
(浙江省湖州市弁南中学)

