度量测度空间上双线性θ-型Marcinkiewicz积分交换子

逯光辉

(西北师范大学数学与统计学院, 甘肃兰州730070)

§1 引 言

众所周知, Littlewood-Paleyg-函数作为调和分析中一类重要的算子, 在调和分析本身以及偏微分方程的研究中发挥着重要的作用(参见文献[1-3]). 而Marcinkiewicz积分本质上就是Littlewood-Paleyg-函数. 在1958年, Stein在文献[4]中引入了高维情形下的Marcinkiewicz积分, 其定义如下

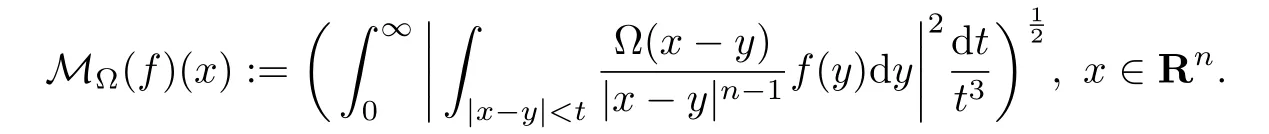
此后, 关于Marcinkiewicz积分及其交换子在不同函数空间上的性质得到了广泛的关注和研究,例如文献[5-9]及其相关的文献.

为了解决Coifman和Weiss意义下的齐型空间(见文献[10-11])和非双倍测度空间(见文献[6,12-15])的统一问题, 2010年, Hyt¨onen在文献[16]中引入了一类新的度量测度空间满足所谓的几何双倍和上部双倍条件(见以下定义1.1和1.2). 方便起见, 现将这类新的度量测度空间简称为非齐型度量测度空间. 此后, 在这类空间上的相关研究受到了很多学者的广泛的关注和研究. 例如,Lin和Yang在[17]中得到了以非齐型度量测度空间为底空间的Marcinkiewicz积分在Lebesgue空间上的一些等价有界性. Cao和Zhou在文献[18]中给出了非齐型度量测度空间上Morrey空间的定义, 且建立了Hardy-Littlewood极大算子, Calder´on-Zygmund算子及Marcinkiewicz积分算子在Morrey空间上的有界性. Xie等在文献[19]中证明了由双线性θ型Calder´on-Zygmund算子Tθ与空间RBMO(µ)生成的交换子[b1,b2,Tθ]在Lebesgue空间Lp(µ)上的有界性. 关于这类新的度量测度空间上的进一步研究和进展可以参看文献[20-29]及其相关的参考文献.

在给出本文的主要结构之前, 首先回顾本文所需的一些概念. 以下的几何双倍和上双倍条件的定义是由Hyt¨onen在文献[16]中引入的.

§2 预备知识

§3 Lebesgue空间上的有界性

§4 Morrey空间上的有界性