某一周期函数类在Orlicz空间内的n宽度

高 媛, 吴嘎日迪

(内蒙古师范大学 数学科学学院, 内蒙古呼和浩特010022)

§1 引 言

宽度问题的研究是函数逼近问题研究中比较难的方面, 研究一些周期卷积类或非周期卷积类的宽度估计问题是宽度问题研究中的重要内容. 王晓丽等在文献[1]中研究了Sobolev函数类在Orlicz空间内的宽度估计问题, 吴嘎日迪在文献[2]中研究了某一周期卷积类在Orlicz 空间内的宽度估计问题. 本文研究了由实系数线性微分算子定义的周期函数类ΩrM在Orlicz空间内的宽度估计问题.

文中用M(u)和N(v)表示互余的N函数. 关于N函数的定义及相关性质见文献[3].M(u)为N函数当且仅当存在定义在[0,+∞)上的实值函数p(t), 使得

其中p(t)满足下列条件.

(1)p(t)为右连续的非减函数;

(2) 当t>0时,p(t)>0;

(3)p(0)=0,p(∞)=∞.

这时p(u)为M(u)的右导数. Orlicz空间L∗M的定义及相关性质见文献[3].G表示n维Euclid空间Rn中有界闭集,u(x),v(x)表示定义在G上的Lebesgue可测实函数. 文中是Orlicz范数,定义如下:

§2 预备知识

命题2.1(见[6]) 设Λ是线性赋范空间X上的一个中心对称的闭凸子集, 则

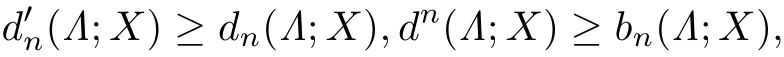
这里dn(Λ;X)(Λ;X),dn(Λ;X),bn(Λ;X) 分别代表Kolmogorov宽度, Linear宽度, Gelfand宽度, Bernstein宽度.

定义2.1若存在n+1个不相交的有序区间I1,··· ,In+1(即对任意x ∈Ij,y ∈Ij+1,j=1,··· ,n,有x

这里ε=±1是固定的, 而且测度m{x:x ∈Ij,f(x)0}>0,则称S(f;[a,b])=n.

记S(f)=S(f;[0,1]).

命题2.2(见[4]) 对于K ∈C([0,1]×[0,1]),h ∈L1[0,1]且0, 令

若K是全正的, 则有S(Kh)≤S(h).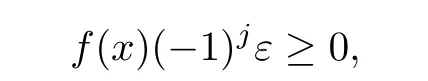

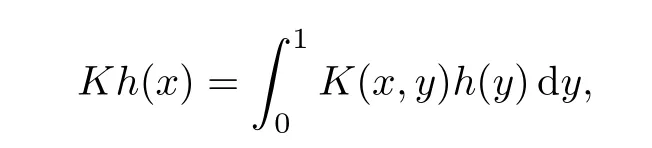
§3 定理及证明