连续广义框架及其对偶的刻画, 冗余及扰动

张 伟, 周 静

(河南财经政法大学 数学与信息科学学院, 河南郑州450046)

§1 引 言

Hilbert空间中的框架概念是在1952年由Duffin和Schaeffer[1]在研究非调和Fourier级数时首先提出的. 1986年Daubechies[2]等突破性的研究引起学者对框架的极大关注和兴趣. 到目前为止, 框架已经广泛应用于图像处理[3], 无线通讯[4], 神经网络[5], 量化测度[6]等领域. 因此, 有关框架的研究成果十分丰富(见[7-12]).

随着框架研究的不断深入, 出现了许多推广形. 特别地, 1993年, 文[13]将框架推广到带有Radon测度的局部紧空间, 引入了连续框架的概念; 2006年, 文[14]提出广义框架的概念;2008年, 文[15]提出连续广义框架的概念使得连续框架与广义框架成为连续广义框架的特殊形式. 本文受文[16]工作的启发, 进一步考虑连续广义框架及其对偶的深刻性质.§2列出连续广义框架及其对偶的定义, 并给出本文用到的连续广义框架的一些基本性质.§3利用相关算子去刻画连续广义框架及其对偶连续广义框架.§4讨论连续广义框架及其对偶连续广义框架的冗余性, 即对任一给定的连续广义框架, 在某些条件下, 去掉部分元素后剩下部分还能构成连续广义框架.§5研究连续广义框架及其对偶扰动的稳定性.

§2 预备知识

本节列出全文所用到的框架的一些记号, 定义和基本性质.

记号:H, U, V表示复Hilbert空间, (Ω, µ)表示赋予正测度µ的测度空间,{Vω}ω∈Ω表示V的一列闭子空间,L(H, Vω)表示由H到Vω的所有有界线性算子的集合, 特别, 如果对于任意ω ∈Ω,有Vω=H, 则记L(H, Vω)为L(H),IH表示H的恒等算子.

§3 连续广义框架及其对偶的刻画

§4 连续广义框架的冗余

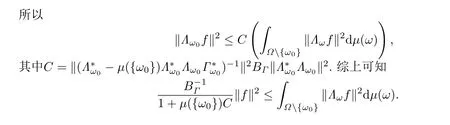
§5 连续广义框架的扰动