矩阵广义迹的计算方法
刘兴祥,武真真
(延安大学数学与计算机科学学院,陕西延安716000)
矩阵的迹是一个古老而又基础的概念,长时间以来,人们一直把矩阵的迹认为是一个方阵对角线上的元素之和,然而一般矩阵也有它自身的迹,我们称之为广义迹。关于矩阵广义迹的运算与其它内容之间的联系有不少学者在这方面研究颇多,而关于矩阵广义迹的计算方法前人未有研究。本文主要是结合矩阵的拉伸运算、乘法运算、Hardmard积以及内积多种运算来研究矩阵广义迹的计算方法,并通过例题验证每种方法的可行性。
1 相关定义

定义2[2]设A=(aij)m×n,B=(bij)m×n,称C=(cij)m×n为A与B的Hadamard积,其中cij=aij×bij,记作C=A∘B。

2 矩阵广义迹的计算方法
矩阵运算之间的关系是矩阵研究中的一个重要内容,而矩阵的迹运算在定义推广之后的研究显得十分重要,下面运用所学知识来探究求矩阵广义迹的几种计算方法。
定理1 (内积法)设A=(aij)m×n,则有
trA=〈csrs(Am×n),
证明采用列顺行顺拉伸运算。如果设

csrs(A)=(a11,a21,…,am1,a12,a22,…,am2,…,a1n,a2n,…,amn)T。
下面关于m,n大小分类讨论:
当m=n时,则
csrs(A)=(a11,a21,…,am1,a12,a22,…,am2,…,a1n,a2n,…,amn)T;

故得
trA=a11+a22+…+amm=
〈csrs(A),csrs(Em)〉。
当m csrs(Am)=(a11,a21,…,am1,a12,a22,…,am2,…,a1n,a2n,…,amn)T; 则有[Em,Om×(n-m)]= csrsEm,Om×(n-m)= 所以有 trA=〈csrs(Am×n),csrsEm,Om×(n-m)〉。 当m>n时,则 csrs(An)=(a11,a21,…,am1,a12,a22,…,am2,…,a1n,a2n,…,amn)T; 综上可得:trA=〈csrs(Am×n), 定理2 (Hadamard积法)设A=(aij)m×n,则有 trA= (其中B为1×m阶1矩阵[1 1 … 1], 下面关于m,n大小分类讨论: 又因为B(A∘Em)C=a11+a22+…+amm, 所以有trA=B(A∘Em)C。 则有trA=a11+a22+…+amm, 则有Am×n∘ [Em,On-m]= 又因为 B(Am×n∘[Em,On-m])C=a11+a22+…+amm, 所以有trA=B(Am×n∘[Em,On-m])C。 则有trA=a11+a22+…+ann, 又因为 综上可得: trA= 当i=j时, 解第一种:(内积法)将矩阵A采用列顺行顺拉伸的形式,即 csrs(A)=(1,0,-1,-,2,1,0,-1,3,2,0,1)T。 由于矩阵A是4×3阶的, (1,0,0,0,0,1,0,0,0,0,1,0)T, 1+0+0+0+0+1+0+0+0+0+0+0=2。 第二种:(Hadamard积法)由于矩阵A是4×3阶的,则取与A相应同型的矩阵, 故得矩阵A迹为 第三种:(类二次型法)由于A为4×4阶的矩阵,对应的有 e44=[0 0 0 1]。 故得


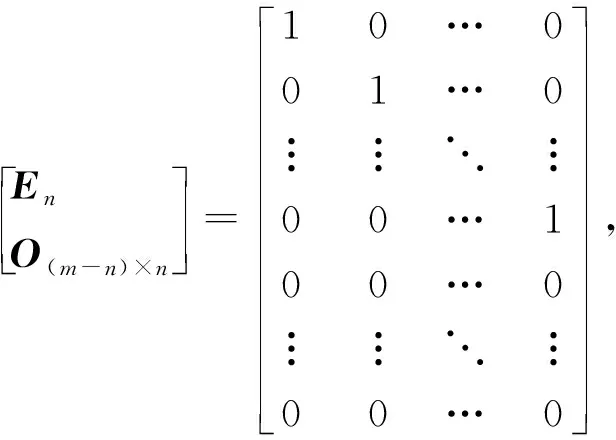


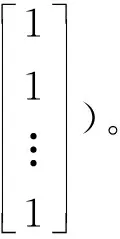







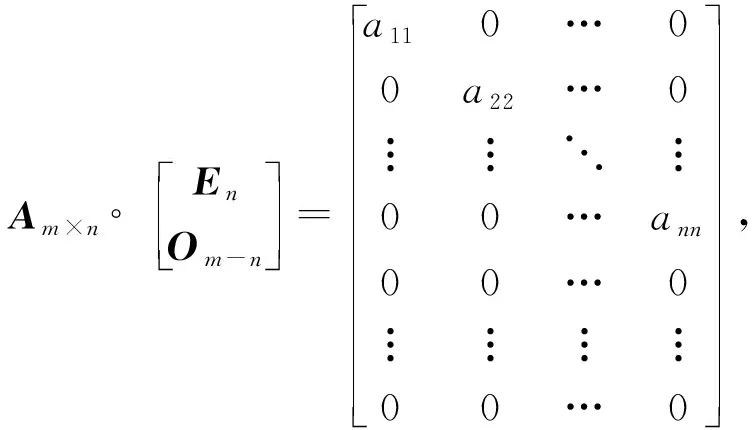

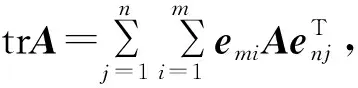






3 举例









