尾架调锥性能的参数化分析与研究

王均涛

（上海昀丰光电技术有限公司 上海200120）

调锥尾架是尾架的一种，在磨削工件时不仅可以对工件起到支撑和定心作用，还可以在头、尾架顶尖中心线发生偏差时，起到调节作用。本文研究的尾架调锥结构如图1所示。当需要调锥时，转动刻度旋钮，刻度旋钮向前移动推动旋转螺杆前进，旋转螺杆迫使锥轴移动，锥轴上装有滚针，滚针滚动挤压圆弧键，圆弧键挤压体壳，使得体壳绕柔性铰链机构转动，完成尾架顶尖的偏移。

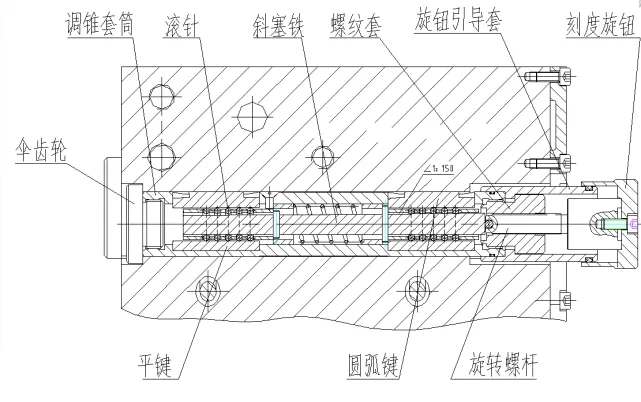
图1 调锥尾架锥度调节原理结构

1 几何模型简化、网格划分及约束施加

在Solidworks中建立尾架的三维模型，如图2所示。调锥尾架的零部件较多，在对尾架进行有限元仿真之前需要对其进行结构简化处理。由于微调过程中，圆弧块随带坡度的斜塞铁的轴向运动仅发生径向的运动，可将微调过程简化为圆弧块与体壳的接触变形过程，因此将几何模型简化为体壳与圆弧块的装配体。同时，将对微调过程的接触变形过程影响很小的几何特征如小圆角、倒角及螺纹孔等进行简化，删除这些细节可以大大减少有限元分析的计算量和求解时间，而不会影响到求解的精度，简化后得到如下图3所示的三维模型。

图2 调锥尾架三维模型图

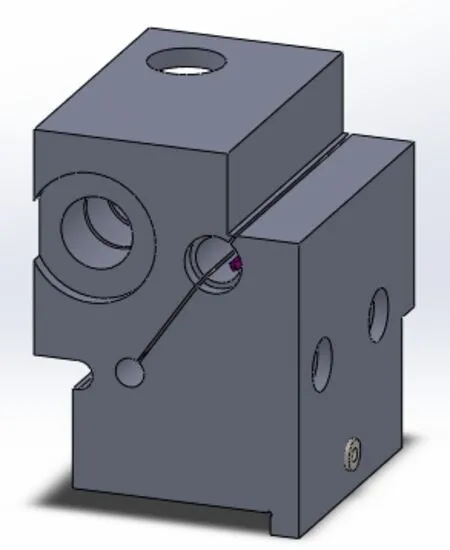
图3 简化后的模型

由于微调过程中，滑块的变形相对于尾架体壳的变形很小，因此可将微调结构简化为圆弧块与体壳的接触变形并对圆弧块只进行离散网格划分计算，在保证模型与实际相符合的同时可减小计算的规模。网格划分结果如图4所示。

根据实际情况对微调结构进行三个方向自由度的约束，如图5所示。在圆弧块与尾架体壳的接触处建立了接触，根据实际情况在模型对应处添加弹簧单元，如图6所示。

图4 微调过程有限元模型

图5 对微调结构进行约束

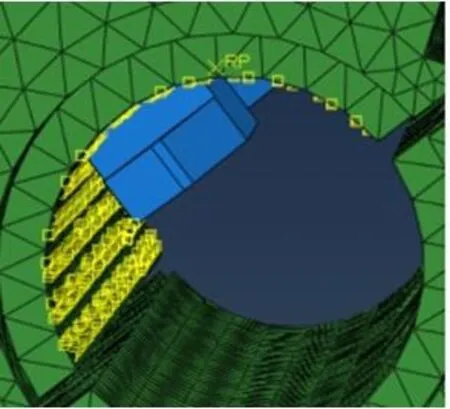
图6 添加弹簧单元

2 尾架调锥参数化结果分析

尾架体壳材料分别选择45钢、HT100、HT200及HT250，依次在不同弹簧刚度（0～800 N/μm）下对圆弧键沿实际微调时运动方向施加0～80 μm位移对简化尾架微调机构的微调运动过程进行了有限元计算。

2.1 在特定条件下，对尾架所受到的的应力、应变、位移分析

在Abaqus下设置弹簧刚度为10 N/mm ，圆弧键位移为40 μm ，对尾架的应力、应变和位移进行了分析计算，分析结果分别如图7、图8、图9所示。由图看以看出，调锥尾架应力与应变最大的位置处于柔性铰链机构处。

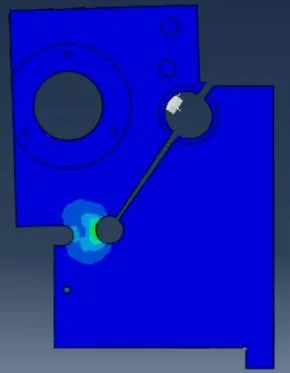
图7 应力分布

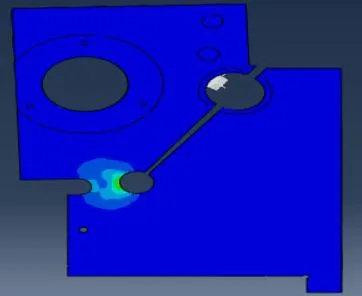
图8 弹性应变分布

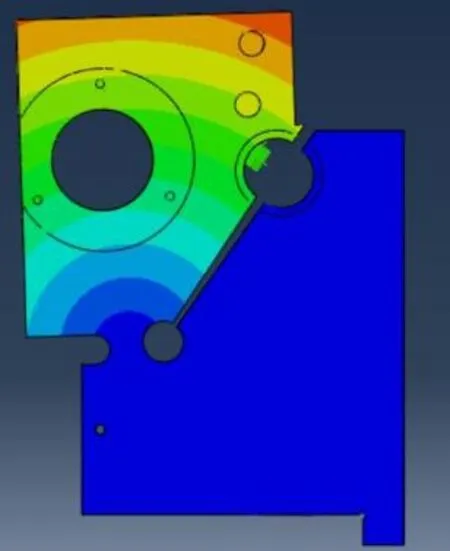
图9 位移分布

2.2 在相同弹簧刚度下，尾架轴线位移随微调量变化的关系

当改变圆弧键位移时，尾架存在水平和垂直两个方向的位移，为了比较这两个方向的位移对尾架的影响，现利用Abaqus对其进行迭代计算。设置弹簧刚度0 ，改变不同的微调量，记录数据汇总如表1所示。为了排除弹簧刚度对尾架轴线位移的影响，现做一组对比试验，设置弹簧刚度为 100 N/mm ，再次迭代计算，获得尾架水平、垂直位移如表2所示。

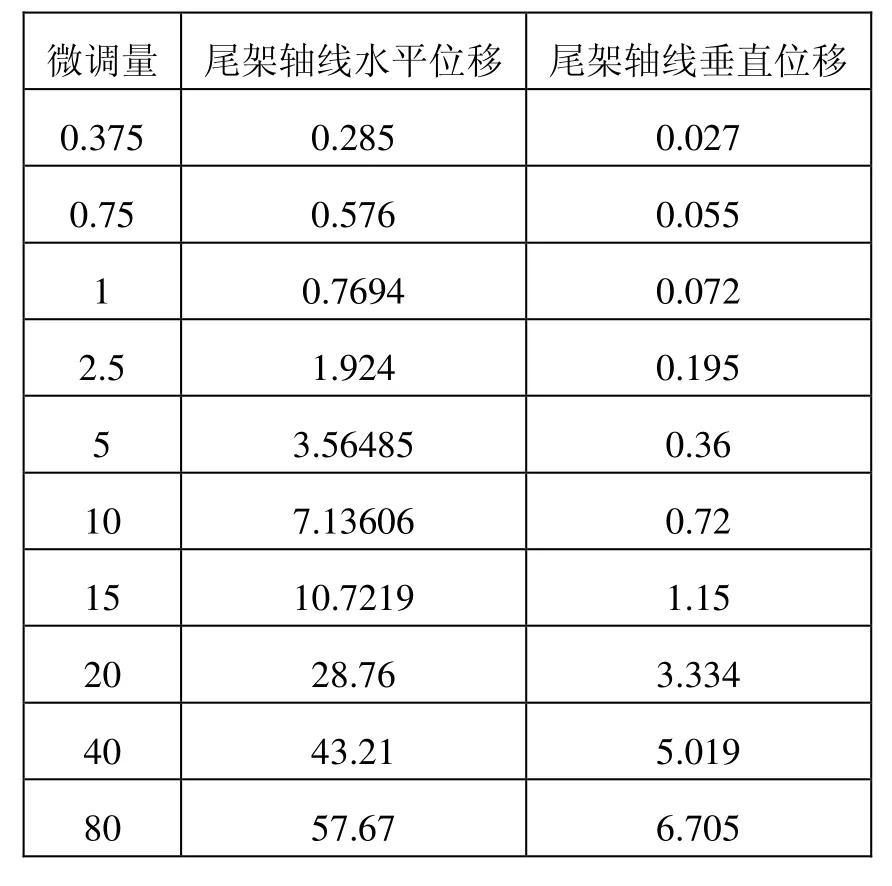
表1 弹簧刚度为0，尾架轴线位移数据(μm)

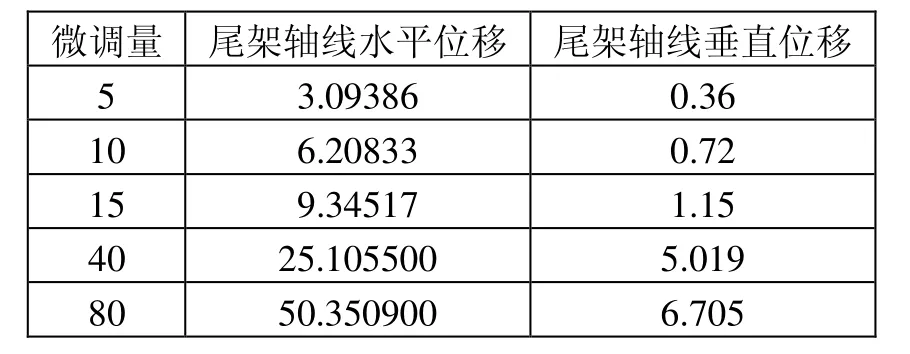
表2 弹簧刚度为100，尾架轴线位移数据(μm)

从表1、表2可以看出，在弹簧刚度一定的条件下，尾架轴线水平方向位移相比垂直方向位移均大了一个数量级，为了便于分析计算，可认为尾架轴线垂直方向位移可忽略。在上述研究的基础上，我们来研究圆弧键位移与尾架轴线位移的关系。通过在Abaqus 中导入模型，此时设置弹簧刚度为0，多次计算，获得不同圆弧键位移下，尾架轴线位移的数据，如表3所示，并绘制关系图，如图10所示。根据表3与图10，我们可以看到，不考虑弹簧刚度时，尾架轴线位移与圆弧键位移呈明显的线性关系，与理论的运动分析相符合。利用数值分析方法中的曲线拟合，以尾架轴线位移为y轴，以圆弧键位移为x轴，关系可用y=ax表示，经过计算得出a≈0.72015 。

表3 弹簧刚度为0，尾架轴线位移与圆弧键位移(μm)

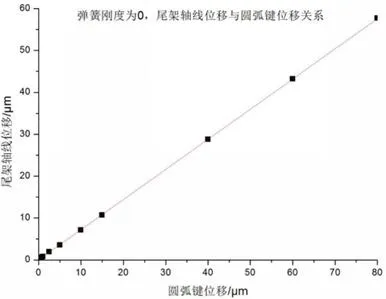
图10 弹簧刚度为0，尾架轴线位移与圆弧键位移关系图

2.3 弹性变形与圆弧键位移的关系

为探究尾架体壳弹性变形对微调过程的影响，获得其弹性变形与圆弧键位移的关系，选取弹性变形最大区域两点A、B，如图11所示。首先，我们在A点用不同的圆弧键位移来测取A点的弹性变形量，记录数据。同理，在B点选取不同的圆弧键位移量测取B点的弹性变形量，记录下测得的数据。根据记录的数据绘制圆弧键位移与A、B两点的弹性形变关系图，如图12所示。

图11 弹性变形最大位置图

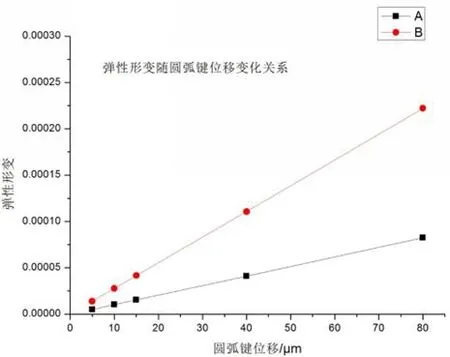
图12 弹性形变与圆弧键位移关系图

可见，A、B点弹性形变均随进给量变化大致呈现线性变化。叠加到几何运动上因而尾架轴线位移与圆弧键位移呈线性变化关系且对比例系数b存在主要影响。弹性形变差与圆弧键位移呈线性关系，可用y=bx表示，利用数值分析理论，拟合曲线，计算得出b≈0.0000016 ，如图13所示。因此弹性变形差与尾架轴线位移也成线性关系，可取比例系数为b的影响评价量。

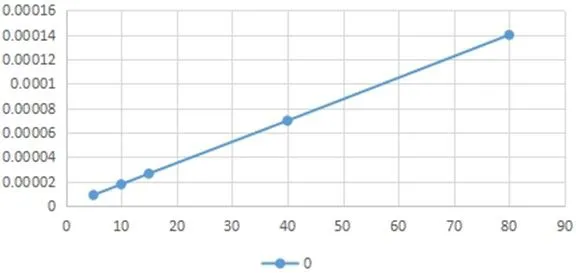
图13 弹性形变差与圆弧键位移关系图

2.4 不同材料对圆弧键位移与尾架轴线位移关系的影响

现在研究在不同材料对圆弧键位移与尾架轴线位移的关系的影响。尾架体壳材料分别选择45钢、HT100、HT200及HT250，在有限元软件中分析计算获取数据，从而绘制出在不同材料下的圆弧键位移与尾架轴线位移的关系图，如图14所示。

从图14看出，弹簧刚度一定时，在不同的材料下，尾架轴线位移与圆弧键位移关系曲线几乎重合，所以材料对圆弧键位移与尾架轴线位移关系的影响很小，可以忽略不计。

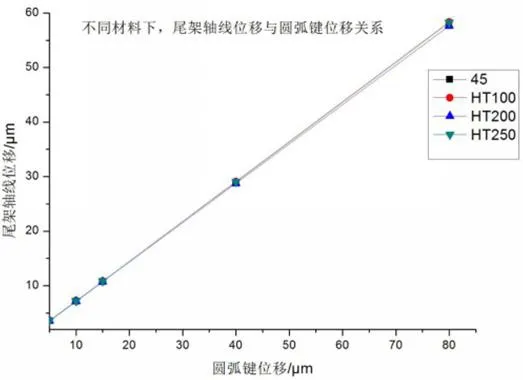
图14 不同材料下，圆弧键位移与尾架轴线位移的关系图

2.5 弹簧刚度对尾架性能的影响分析

经过仿真分析计算，逐步求得不同的弹簧刚度所对应的比例系数，数值计算结果符合理论分析，现将其数据记录如下表4所示。

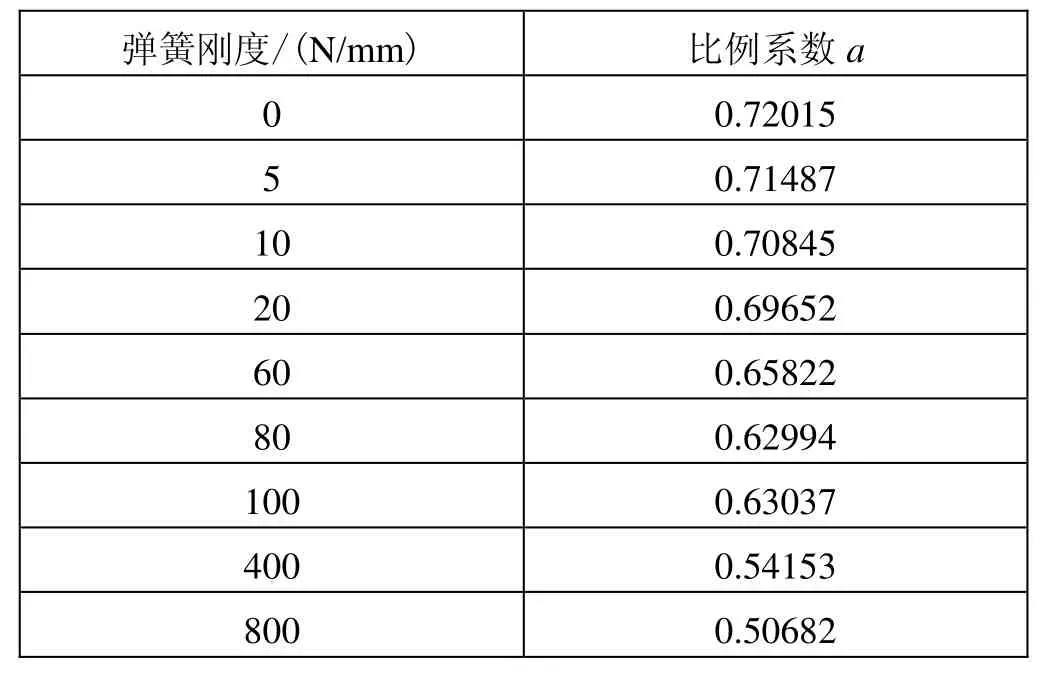
表4 不同弹簧刚度对应的比例系数a

由图15可以看出，随着弹簧刚度增大，尾架轴线位移与圆弧键位移仍保持显著的线性关系，但由表4和图16可以看出系数a随着弹簧刚度的增大而减小，减小的趋势随着刚度增大而减小。

在图17中，对于一定的圆弧键位移，所对应的尾架轴线位移随着弹簧刚度增大而减小，但减小趋势随着弹簧刚度的增大迅速减小，趋于平缓，0～100N/mm 是减小趋势较大区域。

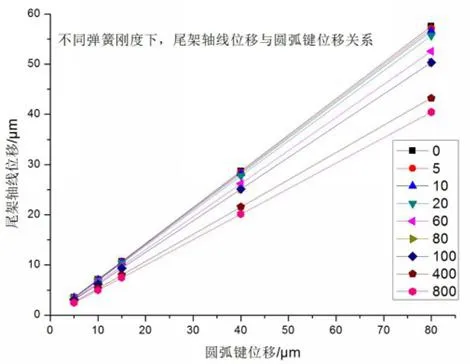
图15 不同弹簧刚度下，尾架轴线位移与圆弧键位移关系图

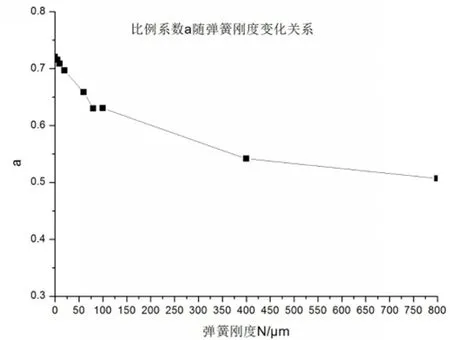
图16 比例系数a随着弹簧刚度的变化关系图

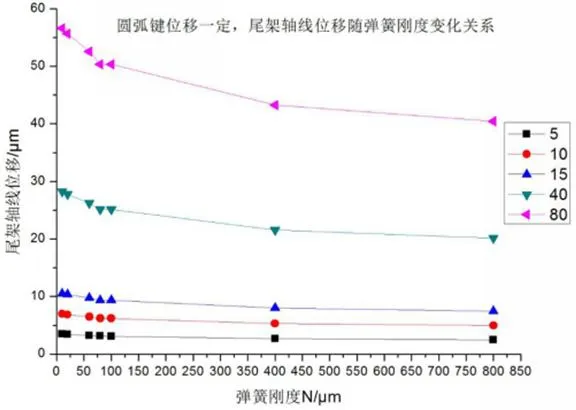
图17 圆弧键位一定，尾架轴线位移随弹簧刚度变化关系图

由图18和图19可见，弹簧刚度通过影响尾架体壳弹性变形情况对尾架轴线位移与圆弧键位移的关系产生影响。可用A、B两点弹性形变差来表示影响的程度。

为了保证圆弧键的设计选择可靠，现在讨论圆弧键位移与弹簧刚度的关系，经过仿真模拟，得到不同弹簧刚度下，圆弧键的接触应力的对应值，弹簧刚度选取0～800 N/mm ，获得数值如表5所示。

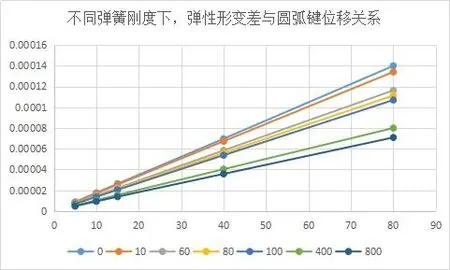
图18 不同弹簧刚度下，弹性形变差与弹性形变差的关系图

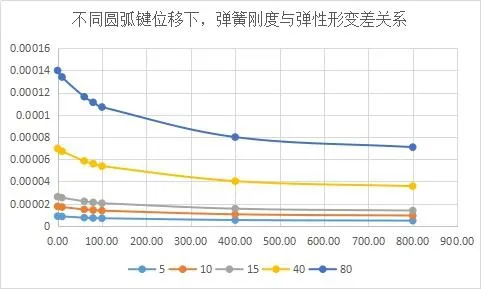
图19 不同圆弧键位移下，弹簧刚度与圆弧键位移的关系图

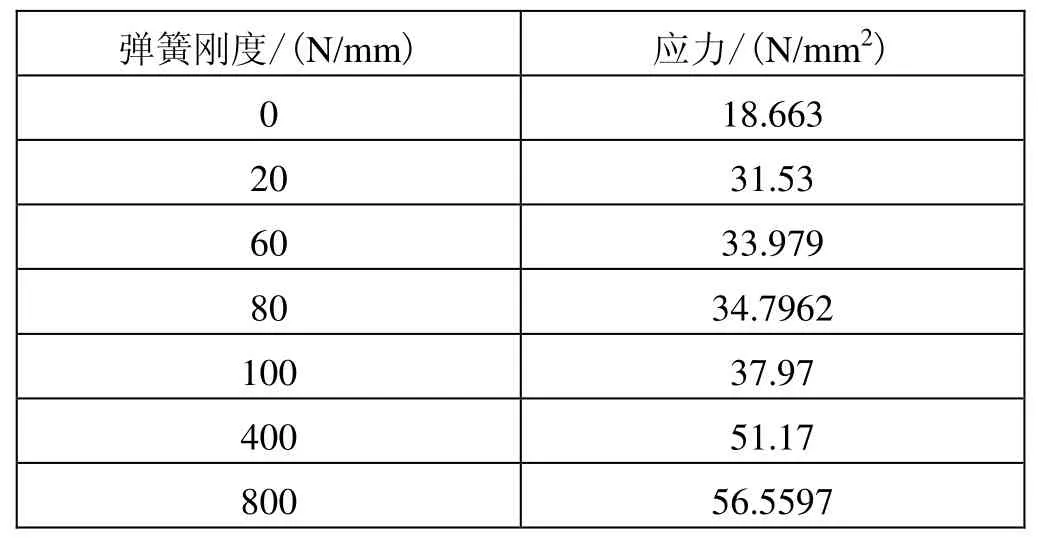
表5 圆弧键的接触应力与弹簧刚度的关系

在图 20 中，横坐标表示弹簧刚度，纵坐标表示圆弧键所受的接触应力，再结合表 3～表 5 可以看出，随着弹簧刚度增加，圆弧键所受到的接触应力基本呈大致增大的趋势，但是趋势越来越平稳，值得注意的是在弹簧刚度达到 20 N/mm和 400 N/mm 的时候，圆弧键所受的应力出现了一小段的急剧跳动，在设计圆弧键时应注意。

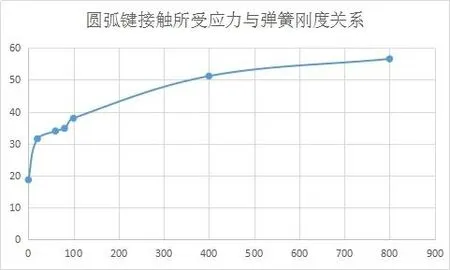
图20 圆弧键所受应力与弹簧刚度的关系图

3 结语

本文通过建立调锥尾架的几何模型，采用Abaqus有限元软件进行参数化的仿真模拟。可得以下结论为调锥尾架设计提供理论支持。

（1）在限制弹簧刚度不变的情况下，研究了尾架位移轴线随微调量变化的关系，水平位移相对于垂直位移高出一个数量级，因此，忽略了垂直位移的变化，简化了分析过程，得出了尾架水平轴线位移与圆弧键位移之间呈明显的线性关系。

（2）选取尾架体壳弹性变形最大的两点，研究了弹性形变与圆弧键位移的关系，为尾架体壳的设计提供了参考。不同的材料在相同力的作用下会产生不同的变形，所以有必要选取不同的材料进行研究，获取尾架轴线与材料的关系。

（3）在不同弹簧刚度条件下，研究了不同弹簧刚度所对应的比例系数a的值，a随着弹簧刚度的增大而减小，减小的趋势随着刚度增大而减小，这样在设计尾架时，就可以选取特定的弹簧刚度，从而得到特定的尾架的轴线位移；还研究了尾架的轴线位移、圆弧键位移和圆弧键的接触应力随弹簧刚度变化的关系。