全相关核偏最小二乘故障诊断方法及在抽油机上应用

汪 波,夏钦锋,钱 龙,彭 军,周 伟†

(1.重庆科技学院智能技术与工程学院,重庆 401331;2.中石化重庆涪陵页岩气勘探开发有限公司,重庆 408000)

1 引言

游梁式抽油机系统是石油生产中最常用的人工举升方法.抽油机的采油过程是一个复杂的工业系统,在抽油杆向地下移动的过程中存在许多未知因素.在采油过程中,由于抽油机系统的不稳定性,容易导致故障发生.一旦发生故障会导致抽油机采油量减少,停产甚至损坏抽油设备.然而,抽油机复杂的工作环境和多变的井下条件使得诊断抽油机故障变得非常困难.因此,为抽油机系统建立精确有效的故障诊断模型是一个具有挑战性和重要意义的工作.

在实际的采油生产过程中,示功图作为一条闭合曲线,反映了抽油杆行程中载荷和位移的关系,是监视抽油机井下运行状况的主要工具[1].在传统的抽油机故障诊断中,工程师通常通过分析示功图的形状来判断井下工作状况,诊断的准确性取决于工程师的经验判断.

近年来,人工智能方法已广泛用于抽油机故障识别与诊断.这些方法包括粗糙集理论[2]、人工神经网络[3–4]、支持向量机[5–6]等.但是,这些方法主要使用载荷和位移数据来诊断井下工作条件.如今,随着油田信息化建设的发展,油田企业已经积累了大量的生产数据,包括电压、电流、油压、采出液量、功率因数和泵效率等.在抽油机采油过程生产中,这些大量的生产数据为抽油机故障诊断提供了可能.

近年来，数据驱动的故障诊断方法广泛应用于工业系统诊断中[7–8].其中,多变量统计过程监控(multivariate statistical process monitoring,MSPM)具有较强的变量间相关性解释能力,被广泛用于复杂工业过程的故障诊断[9–10].MSPM方法通常限于显著利用的偏最小二乘(partial least squares,PLS)的方法[11–12].基于PLS模型,已经开发了许多成功的监视方法[13–14].这些方法从大量输入和输出数据中提取潜在特征,从而可以有效地消除回归中的无效噪声,用以诊断工业过程中的故障.同时,PLS可以提取更少的组件来解释更多与变量相关的问题.近年来,李刚等人[15]揭示了用于过程监控的PLS的几何性质.根据李刚的结果,周东华等人[16]首先分析了用于质量相关故障检测的PLS的固有缺陷,并提出了具有更详细分解过程变量矩阵的总PLS(total PLS,T-PLS)模型.但是油井的生产过程表现出非线性、参数耦合和时变等特点,因此很难使用传统PLS算法建立准确的抽油机故障诊断模型[17].

为了解决过程数据的非线性问题,Rosipal等[18]人提出了一种非线性核PLS(kernel PLS,KPLS)方法,将非线性输入数据映射到高维特征空间中.彭开香等[19]人提出了一种基于KPLS模型的与质量有关的非线性故障检测方法TKPLS(total KPLS,TKPLS).文献[20]提出了一种改进的KPLS算法,以提高质量相关故障的检测精度,并降低质量无关故障的误报率.文献[21–22]提出了一种基于最优偏好矩阵的改进KPLS方法来解决主成分误解的问题.最优偏好矩阵用于调整过程变量的分布和协方差矩阵的特征值.文献[23]中,提出了一种基于多块KPLS的分布式故障诊断方法来监视大型工业过程.文献[24]开发了一种时间片批处理监视方法来解决线性和非线性变量的问题.

尽管KPLS和相应的扩展方法已广泛用于过程监视和故障诊断,仍亟需解决以下问题:1)在KPLS模型中,通过离线数据得到的静态数学模型不能及时反映数据之间的相关性,且不能准确描述与变量相关联的潜在特征的变化.2)由于时变特性和工业变量参数的多重相关性,传统KPLS不能完全提取变量之间的隐藏特性,导致诊断精度低.

受到多元统计方法的启发,本文提出了一种新颖的全相关动态核偏最小二乘(fully-correlated dynamic kernel partial least squares,FCDKPLS)故障诊断算法,并应用于抽油机系统的故障诊断.首先,基于自回归模型(auto regressive,AR)建立输入和输出变量的强动态相关特性,从而反映变量之间隐藏的动态关系;其次,通过分析证明KPLS模型的输出变量影响到输入残差子空间,为此构建输出变量辅助矩阵,表征输出与输入向量全相关,从而直接反映输入与输出变量的关联性.实验结果表明,本文提出的方法在抽油机故障诊断上具有良好的诊断效果.

2 自回归模型

在抽油机系统中,一个因变量总是和多个自变量有关,且数据中输入变量与输出向量之间存在着时序相关性.为表征抽油机数据动态特性,对数据建立AR模型:

其中:x(ϑ)为抽油机数据变量,α1,α2,···,αn为模型回归系数,εϑ为模型随机误差,h为模型阶次.令

则AR模型表示为

从而可以求得模型系数矩阵.

AR模型解决自相关问题在于确定模型阶次h,可以根据贝叶斯信息准则来确定最合适的阶数.若要得到更为精确的时滞阶次,可利用统计假设检验[25]判断各个变量是否具有自相关性.

通过构建AR模型,反映数据变量间的动态关系,然后对动态扩展数据进行KPLS分析.

3 FCDKPLS算法

3.1 KPLS算法

KPLS通过非线性映射函数Φ(·)将其转换到高维特征空间F中,在特征空间中构建PLS回归模型.设{(X1,Y1),(X2,Y2),···,(Xn,Yn)}⊂RL1×RL2,N为训练样本个数,L1为输入变量个数,L2为输出变量个数.输入与输出向量分别建立回归模型如下:

其中:i表示KPLS中保留的隐变量个数,通过交叉检验得到;ti为输入向量的得分矩阵,pi为输入向量的负载矩阵,qi为输出向量负载矩阵,φi和εi分别为输入和输出向量残差矩阵.KPLS算法流程如算法1所示[26].

算法1KPLS算法.

1) 初始化ui;

2) 计算Φ(x)的得分矩阵:

3) 计算输出负载矩阵:Pi=YTti/‖ti‖;

4) 计算负载主元ui:ui=Y Pi;

5) 重复2)–4)步直至ti收敛;

6) 计算残差矩阵K和Y:

7) i=i+1,返回步骤2).

3.2 KPLS相关性分析

在KPLS中,输入残差子空间φi(x)与输出向量Y存在着相关性:

其中:ti为KPLS中的主元空间部分,φi(x)为KPLS中的残差部分.当il时

结合式(5),式(4)可以表示为

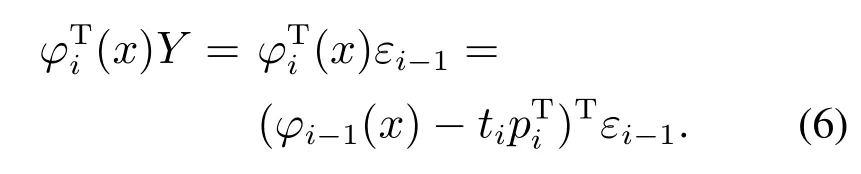
在KPLS中输入和输出向量的负载向量pi和qi分别可以写为

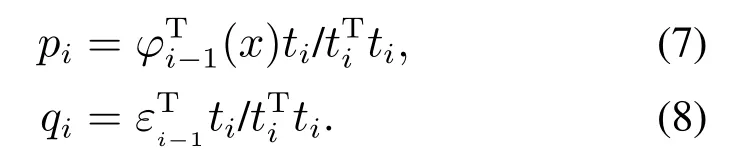
将pi和qi代入式(6)得到

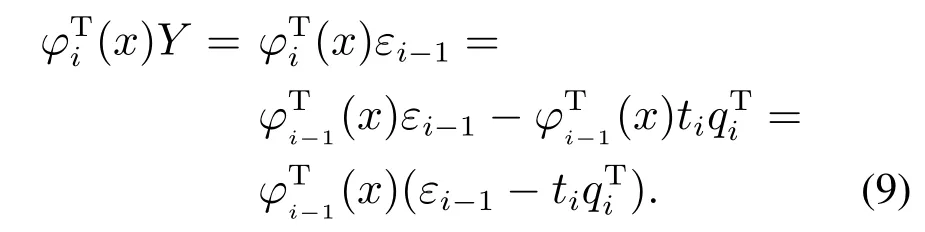
通过式(9)可知输入残差与输出变量之间具有一定的关系.具体关系如图1中的步骤2所示,φi(x)与εi呈垂直状态.假定残差向量子空间与输出向量之间没有关联,即=0.由于ti与εi为垂直状态,说明在模型进行第i −1次迭代时t与ε正交,同理,第i次迭代时,.由于模型的迭代次数不同,模型内部第i次迭代时的主元空间与第i−1次迭代时的残差空间之间的联系不清楚,从而无法确保ti与εi−1是否满足正交原则.实际上,.因此,KPLS中输入变量残差子空间与输出变量之间存在着相关性.

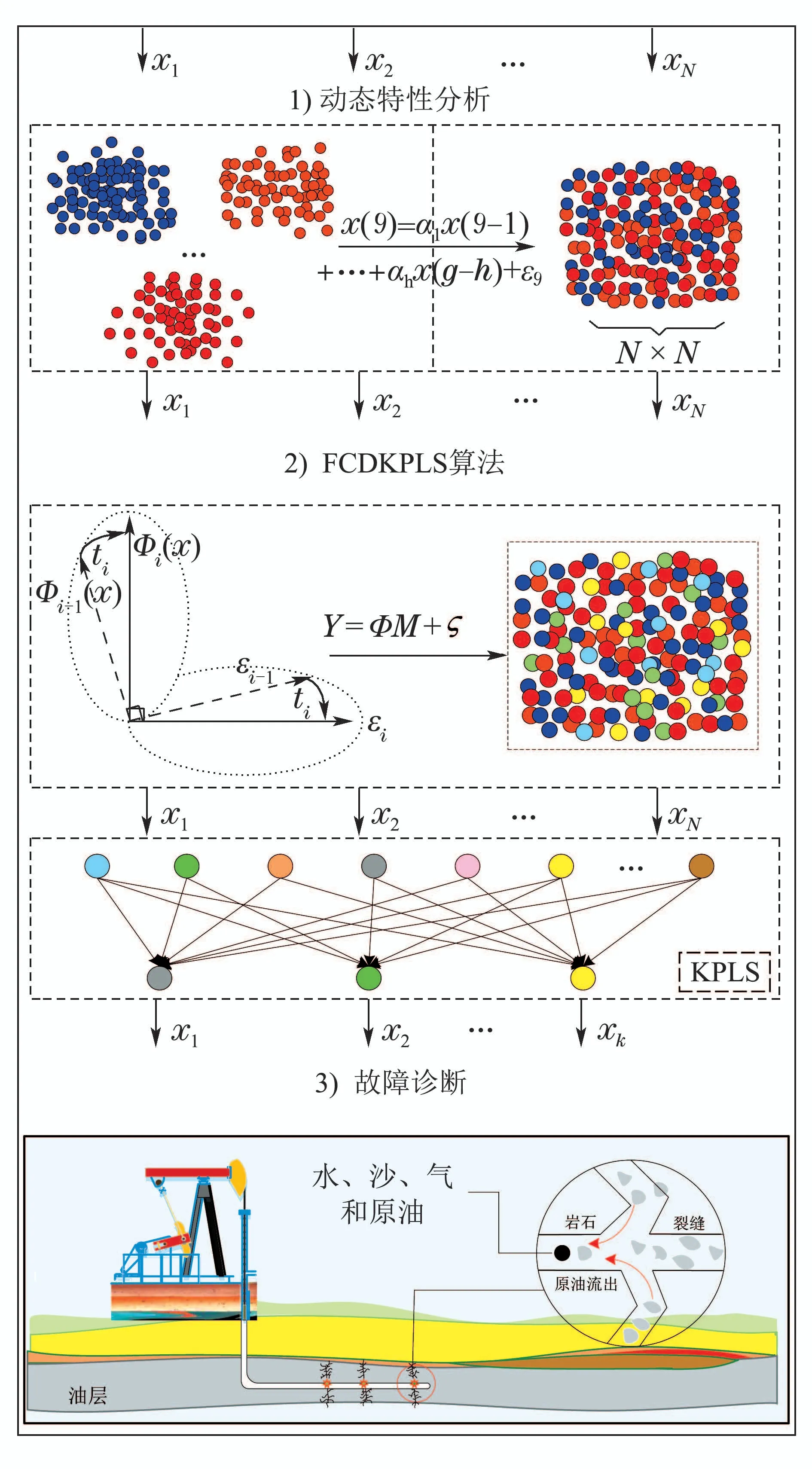
图1 基于FCDKPLS的故障检测过程Fig.1 Fault detection process based on FCDKPLS

3.3 输出变量全相关辅助矩阵

把生产数据分为输入Φ(x)∈Rn×L1和输出Y ∈Rn×L22个矩阵,并在输出变量中构建辅助矩阵M,包含满Φ(x)与Y 的相关性,建立与输出变量相关的全相关矩阵,构建如下回归模型:

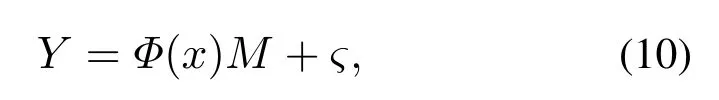
其中:M为构建的辅助分解矩阵,将原始输出向量映射到特征空间中重新进行输入与输出向量的非线性分解;ς为Φ(x)完全不相关的噪音或干扰.

对于M的构建,有

实际上,由于Φ(x)可以任意大甚至是无限大,因此上述公式不能直接用于计算.为了避免使用Φ(x),定义以下内核矩阵K 是一种常见的方法,高斯核函数[27]进行运算:

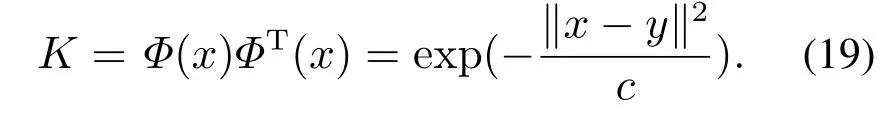
为说明构建的辅助分解矩阵能表征输入和输出变量之间的相关性,这里采用拉格朗日乘子法进行分析证明.

首先,分别标准化Φ(x)和Y 为X0和Y0,拉格朗日乘子法如下:

其中I为单位矩阵.因此,得到输入残差与输出变量的结果收敛,使构造的辅助矩阵可以表征输入向量与输出变量之间全相关性.

3.4 FCDKPLS算法

上述理论推导了输入变量与输出变量存在全相关性,依据AR动态特性,构造辅助分解矩阵模型,使数据间输入和输出变量之间的相关性被充分挖掘.故障诊断步骤包括离线主元模型、在线故障诊断,FCDKP LS算法流程如算法2所示.

算法2FCDKPLS算法.

1) 构建AR模型系数矩阵α;

2) 计算全相关辅助矩阵M:

3) 初始化ui;

4) 计算输入向量得分矩阵:

5) 计算输出向量负载矩阵:Pi=MTti/‖ti‖;

6) 计算负载主元ui:ui=MPi;

7) 重复3)–6)步直至ti收敛;

8) 计算残差矩阵K和Y:

9) i=i+1,返回步骤4).

首先,对归一化后的变量进行动态特性分析,以获得变量的隐藏动态关系.其次,构建FCDKPLS模型,使数据间在输入残差与输出变量之间提取更多地潜在变量.最后,将FCDKPLS模型用于实时数据分析,并将获得的主元用于故障诊断.FCDKPLS算法的故障诊断与监测过程流程图的具体步骤如图1所示.

根据图1所得FCDKPLS故障检测过程流程图,分别给出离线建模和在线监测步骤:

A 根据正常情况建模.

①获得观测数据子集;

②用每个变量的均值和标准偏差来规范化数据子集;

③根据规范化的数据计算核矩阵,并计算中心化核矩阵K;

⑤进行时滞阶次分析,提取动态非线性关系;

⑥建立全相关辅助矩阵M,结合KPLS方法得到主元;

⑦确定控制界限.

B 在线监测.

①在线采集观测变量数据;

②用每个变量的均值和标准差来规范化数据子集;

③计算规范化后的在线观测数据的核向量,计算中心化核向量;

④时滞阶次分析,提取动态非线性关系;

⑤得到的统计量与模型得到的控制限进行比较,当超出控制限后,进行故障源的追溯与判别.

4 基于FCDKPLS算法的故障检测方法

通过上面算法求出m个主元的隐变量的得分向量T=[t1t2··· tm], U=[u1u2···um]以及负载向量P=[p1p2··· pm], Q=[q1q2···qm],再选取了其中m个主元后得到Φ(x)和输出Y 的重构数据和及相应的重构误差矩阵.

定义在第i 时刻的平方预测误差(squared prediction error,SPE)可以写为

其中:g是一个加权参数,h是自由度,a和b分别是SPE(i)的估计均值和方差.

Λ是得分矩阵的协方差,则T2统计量控制限计算公式为

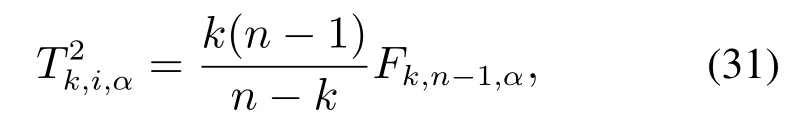
式中:α为显著性水平,n为数据采样次数.

5 实验研究

在本节中,通过大港油田实际生产数据来验证本文提出的FCDKPLS算法的有效性.在石油开采过程中,当抽油机中某个阀门或者某处电压不稳定时,都会引起连锁故障,从而降低采油效率,甚至损坏设备,带来严重的经济损失和人员伤亡.因此,需要对抽油机采油过程中的各个参数进行实时监控,及时监测可能发生的故障,从而有效地减少故障,实现高效采油.

本文主要以抽油机生产过程中的3种典型故障为例进行实验分析:故障1是连抽带喷故障,故障2是疑是杆脱落故障,故障3是气体影响故障.连抽带喷故障是由于油井的自喷能力,在抽油过程中,柱塞基本不受载荷作用,示功图载荷和位移的大小取决于油井喷势的强弱和原油的粘度.在此过程中主要由出口阀漏油影响,故障发生时影响电压、电流、有效冲程、喷射和产生流体量等参数.疑是杆脱落故障是由于抽油杆弹性疲劳、抽油杆丝扣没有上紧、抽油泵遇卡等原因使得抽油杆超过其拉伸屈服极限导致的.由于摩擦力的作用,使得上、下载荷线不重合.在此过程中主要由载荷影响,故障发生时影响电压、电流、有效冲程、泵输出和最大、最小载荷等参数.气体影响故障是当抽油泵中的油液混入较多气体时,在上冲程过程中,由于油液内混有气体的因素,使泵腔内压力在该下降的时候不能正常下降,导致固定凡尔开启时间延后,使得抽油杆加载速度变慢;在下冲程过程中,泵腔内的压力变化和上冲程过程恰好相反.在此过程中主要由压力影响,故障发生时影响电流、冲程、泵效率和有功功率等参数.

抽油机采油过程中产生了大量的生产数据,本文主要提取示功图数据、电流、电压等生产数据用于FCDKPLS算法建立故障诊断模型.笔者从中石油大港油田2017年1月1日至2017年12月31日生产数据中提取构建了2000组数据集,其中训练数据集由1500组数据组成,测试数据集由500组数据组成.由于示功图由144个载荷和位移数据构成,直接用于建模会导致输入数据过大.因此,首先利用傅里叶描述子方法对示功图数据进行特征提取,提取出21个特征数据表征示功图特征[28].每个数据集由41个变量组成，其中32个变量作为输入变量,包括油压、套压、采出液量、出口阀漏油、喷射、流体量、有效冲程、泵输出、最大负荷、最小负荷和21个示功图特征数据.9个变量作为输出变量,包括三相电流、三相电压、功率、泵效率和载荷.在训练数据集中,前1000个数据集是正常的,后500个数据集是故障样本.在测试数据集中,前300个数据集是正常的,后200个数据集是故障样本.

对于故障1,检测结果如图2所示.

图2 故障1的检测结果比较Fig.2 Comparison of detection result in fault 1

当泵效率发生变化时,从图2(a)可以得出,KPLS中T2和SPE统计量均在第300个样本处发生跳变.在T2中,正常样本大多数能低于控制限;在故障样本中,较多故障样本低于控制限,故障诊断效果较差.在SPE中,几乎所有正常样本低于控制限.但在故障样本中,大多数故障样本低于控制限,致使检测效果差.图2(b)中,FCDKPLS中均能在第300个样本处检测到故障.同时,T2和SPE正常样本超过控制限均很少,故障样本绝大多数超过控制限,诊断效果较好.

图2(b)可以成功检测到故障,证明输入向量残差子空间的变化确实受到输出变量的影响,检测故障精度高.但当检测到故障后无法对故障源进行定位.因此,本文引用贡献率来进行故障定位,而传统的贡献图在进行多变量故障定位时,故障变量会受到与之相关性较强的变量的干扰,存在某些时刻正常变量贡献值大于故障变量的情况,容易得到错误的结果.在此基础上,本文引用累积贡献率对故障源进行追溯定位,以此来确定故障源.第i时刻j个样本数据的累积残差贡献率[29]定义为

基于T2统计量的贡献率定义如下[30]:

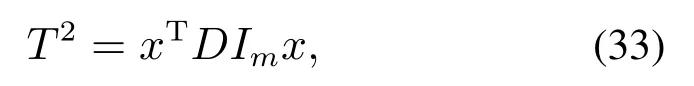
式中D=PTΛ−1P.

在故障1中,引起连抽带喷故障的主要原因是由出口阀漏油引起的,与其相关的故障变量有电压、电流、有效冲程、喷射和产生流体量等参数.从图3中可以看出,图3(a)的T2和SPE统计量的故障源均为喷射(变量37)引起,而图3(b)在T2中故障由出口阀漏油(变量30)引起,SPE中由喷射(变量37)引起.而在实际采油过程中,故障1往往由出口阀漏油所致,即变量30引起,所以本文提出的方法可以准确定位故障源.

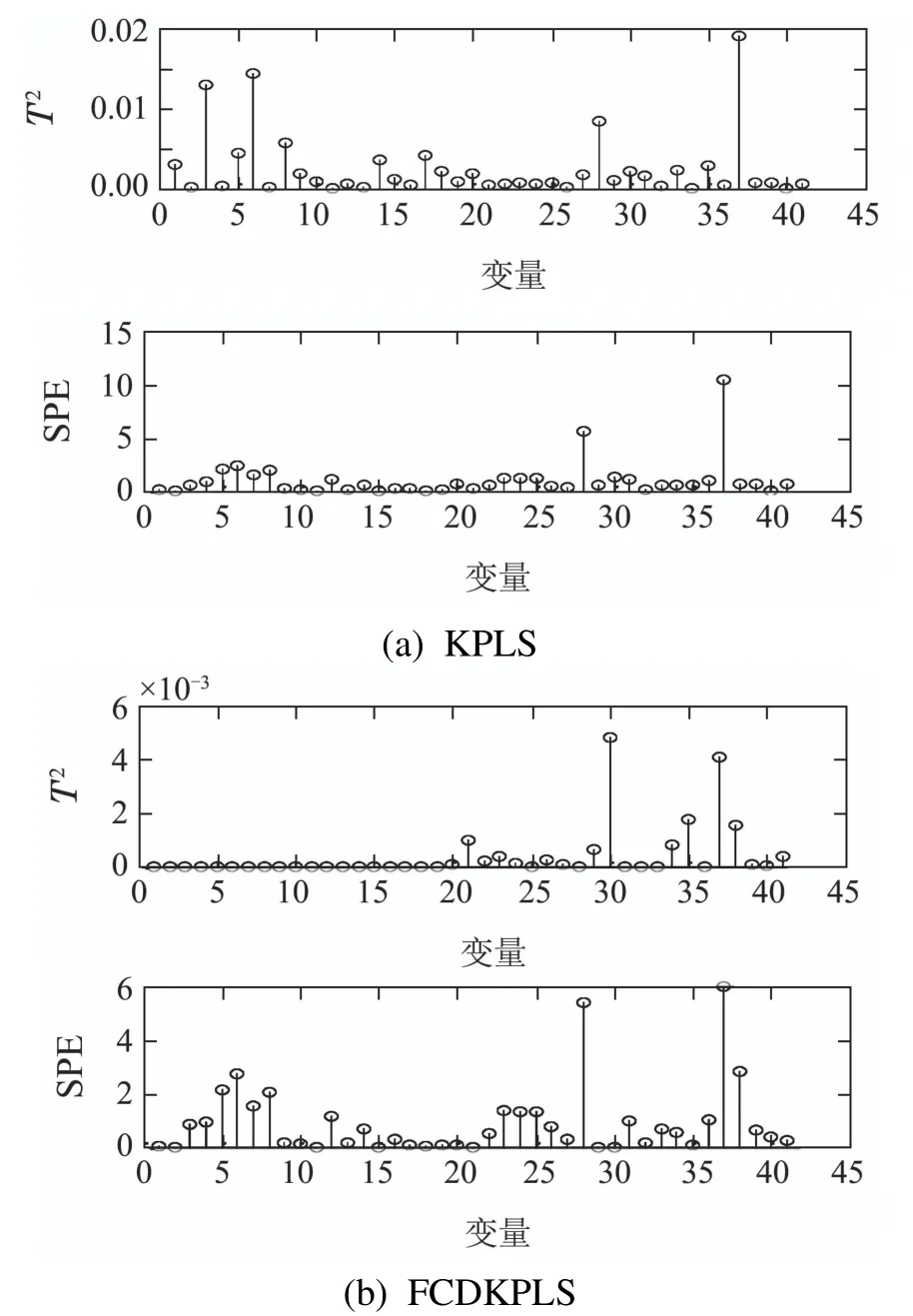
图3 故障1的变量贡献率比较Fig.3 Comparison of variables contribution rate in fault 1

对于故障2,监测结果如图4所示.当载荷发生变化时,图4(a)中T2和SPE统计量均能在故障点300处发生变化,但T2中绝大多数故障样本未超过控制限,不能良好进行故障诊断.SPE中,正常样本超过控制限较多,同时故障样本未超过控制限也比较多,在检测过程中不能良好的进行故障诊断.不能正常进行故障检测.如图4(b),T2和SPE统计量均有良好的故障诊断效果,与KPLS相比,FCDKPLS方法在监测故障2方面更有效.同时,也证明了在提取出所有相关特征后,故障诊断的精度明显增加.

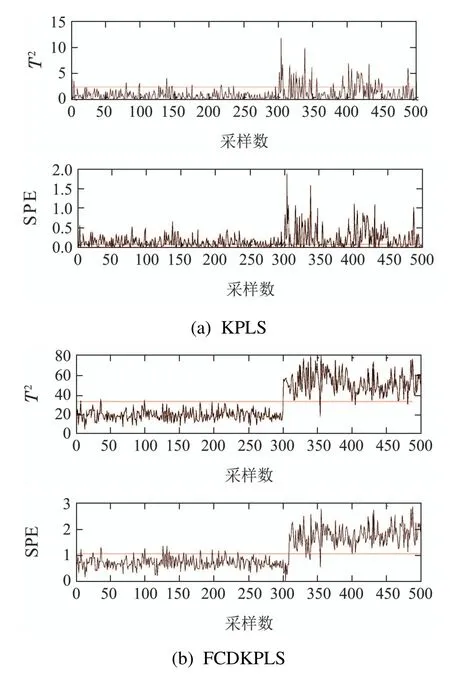
图4 故障2的检测结果比较Fig.4 Comparison of detection result in fault 2

在故障2中,引起疑是杆脱落故障的主要原因是由载荷引起的,与其相关的故障变量有电压、电流、有效冲程、泵输出和最大、最小负荷等参数.从图5中可以看出,图5(a)中T2的故障源为有效冲程(变量8),而SPE的故障源为最小载荷(变量28);图5(b)在T2中故障由最大载荷(变量21)引起,SPE中由最小载荷(变量28)引起.在疑是杆脱落故障中,故障源往往由最大载荷所致,即变量21所引起,从而验证所提出的方法可以对故障进行检测并帮助其对故障源进行准确定位.

通过对抽油机生产过程数据进行统计过程监控,利用KPLS和FCDKPLS算法得到的各变量的贡献率,最终用T2和SPE 统计量的误报率(FPR)和漏报率(FNR)作为衡量监控性能的指标,结果如表1所示.在多故障分类中,计算故障的误报率和漏报率时,其他故障样本被认为是“正常样本”.所以,误报警率是被识别为正常的“故障样本”的数量与正常样本的总数的比率;漏报警率是故障的“正常样本”的数量与故障样本的总数的比率.由表分析可知,基于FCDKPLS方法的多元统计过程监控方法在抽油机生产过程故障检测与诊断方面具有良好的监控性能,适用于复杂的非线性和动态工业过程.

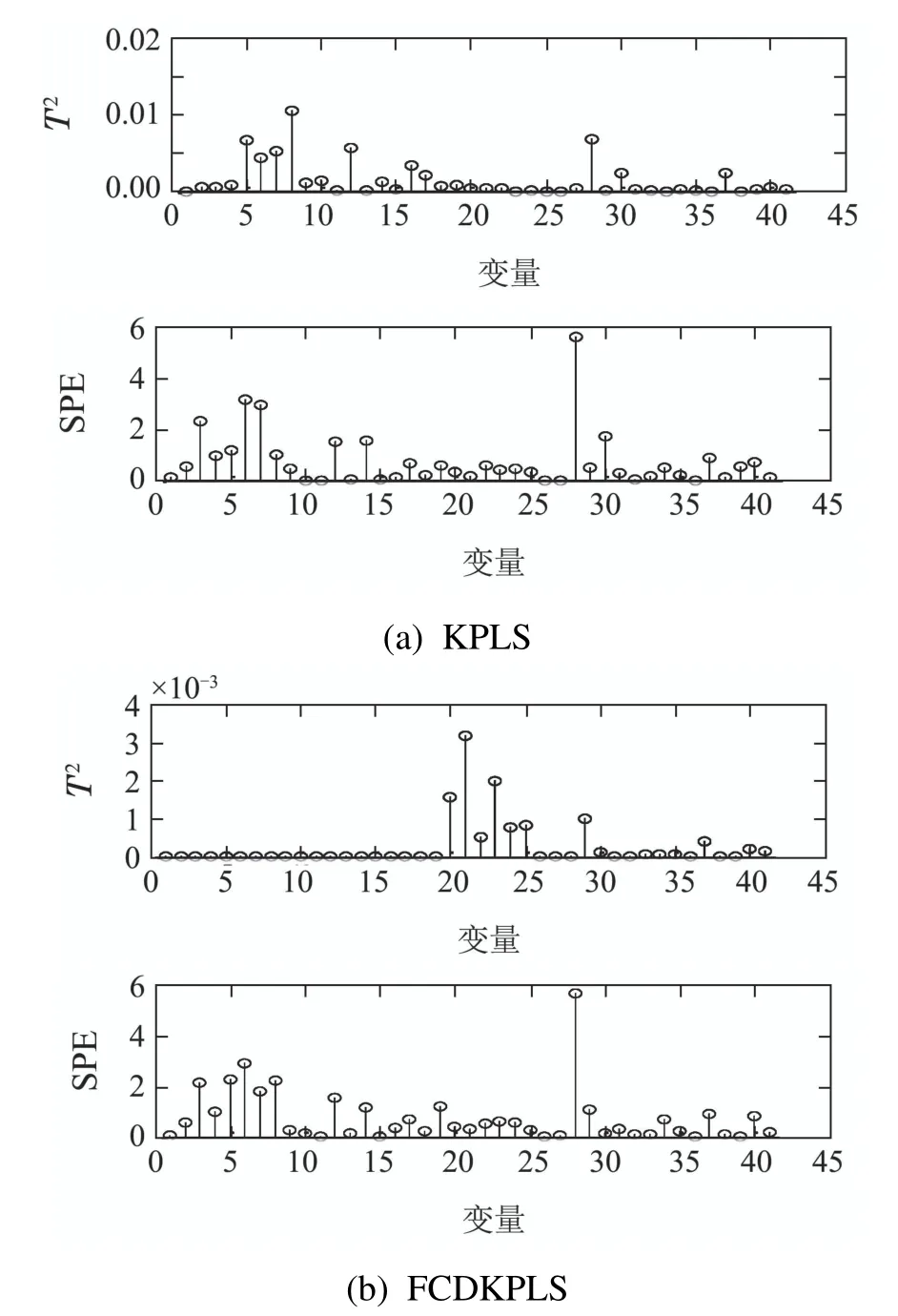
图5 故障2的变量贡献率比较Fig.5 Comparison of variables contribution rate in fault 2

表1 误报率、漏报率(%)比较Table 1 Comparison of FPR and FNR

6 结论

本文提出一种全相关动态核偏最小二乘的抽油机故障诊断方法.首先,分析抽油机数据的动态特性,建立了自回归模型,有效挖掘数据间存在的潜在变量,使数据间具有强动态性;其次,分析证明了KPLS输入残差子空间与输出变量之间具有相关性,在输出变量上构造辅助矩阵,使输入变量残差矩阵与输出变量无关,得到输入变量与输出变量全相关特性.实验结果证明了FCDKPLS监测方法比传统KPLS监测方法表现出更好的监测性能,表明所提出的FCDKPLS监测方法对于抽油机过程监测的有效性.