基于局部熵双子空间的多模态过程故障检测

郭金玉,刘玉超,李 元

(沈阳化工大学信息工程学院，辽宁沈阳 110142)

1 引言

近年来,在人工智能和大数据的时代背景下,工业生产过程也逐渐趋于大型化、自动化和智能化,这就需要对控制系统具有更高的要求.为了有效提高控制系统故障检测性能,基于数据驱动的多元统计分析方法在工业过程领域迅速发展[1–7].数据驱动方法仅依赖于工业生产中所获得的历史数据来建立监控模型,不需要依赖先验知识和数学模型,从而得到了广泛的关注.

主成分分析(principal component analysis,PCA)算法是典型的基于数据驱动的故障检测算法.PCA算法[8–10]是一种线性降维的方法,该算法将原始过程数据划分为两个正交子空间,通过分析低维主成分子空间和残差子空间进行故障检测.PCA算法应用平方预测误差(square predicted error,SPE)和T2对样本状态进行监控,但是应用SPE和T2统计指标时需要数据服从多元高斯分布,因而PCA在非高斯过程中的故障检测效果不理想.为了克服PCA的局限性,Mohamed等人[11]提出一种基于高斯框架的故障检测方法,在数据服从高斯网络条件下,引入PCA方法和二次检验统计量,该方法虽然一定程度上提高了系统的故障检测率,但是依然不适用于非高斯过程.为了提高非高斯过程的故障检测率,Kano等人[12]将独立成分分析(indepen-dent component analysis,ICA)应用于故障检测领域.ICA假设原始样本相互独立,不要求数据服从高斯分布.为了进一步提高非高斯过程故障检测率,国内外学者将PCA与ICA结合提出一些改进算法.为了有效地提取工业过程的高斯和非高斯信息,提高故障检测性能,Ge等人[13]提出一种基于独立成分分析–主成分分析(independent component analysis-principal comp-onent analysis,ICA–PCA)的检测方法,通过提取数据集的主成分和独立成分,根据距离相似度作为统计量,提高故障检测性能.为了找出工业过程中引起故障发生的主要变量,Zhong等人[14]提出一种基于独立成分分析和主成分分析的回归算法,该方法通过建立ICA–PCA模型,提取数据的高斯特征和非高斯特征,对结构相关的统计量进行在线故障检测.对基于ICA–PCA模型获取的过程状态和故障信息,进一步建立基于LASSO回归算法的故障诊断模型结构,从而实现对引起主要异常变量的故障进行定位和选择.为了解决工业生产过程数据服从不同分布问题,Huang等人[15]提出一种基于变量分布特征的统计过程检测方法,该方法首先采用d检验来识别过程变量的正态性,分别建立了用于高斯子空间和非高斯子空间故障检测的PCA和ICA 模型,再用贝叶斯推理将两个子空间的检测结果进行统一,提高故障检测性能.以上对PCA和ICA的改进算法可以有效地提高非高斯过程的故障检测率,但是这些方法仅适用于单一模态的故障检测,对于工业生产过程中存在的多工况、多模态等问题,其故障检测能力下降.为了提高工业系统的控制过程,Zhao等[16–17]提出一种动态分布式监控策略,将动态变化从稳态中分离出来,同时对其进行监测,以区分控制系统运行过程的正常状态和实际故障的变化.为了提高多模态非高斯过程的检测性能,Xu等人[18]提出一种动态贝叶斯独立成分分析(dynamic Bayesian ICA,DBICA)方法,该方法利用矩阵动态增强技术从原始数据中提取动态信息,然后将贝叶斯推理和ICA相结合,建立了多模态非高斯数据的概率混合模型,从而进行故障检测.为了提高多模态非高斯过程的无监督作用,Ge等人[19]提出一种基于贝叶斯推理和两步独立成分分析–主成分分析特征提取策略的多模式过程无监督方法,该方法利用PCA进行特征提取和降维,利用贝叶斯推理将传统的检测统计量转化为各运行模式下的故障概率,通过检测数据样本的后验概率和联合概率,确定数据是否正常.为了提高ICA在多模态过程中的检测性能,一种基于局部熵独立成分分析的过程监控方法(local entropy independent component analysis,LEICA)由Zhong等人[20–21]提出,该方法通过将数据转换到局部熵空间,建立ICA模型,实现故障检测.本文为提高具有多模态和非高斯特征的工业过程故障检测效果,提出一种局部熵双子空间(local entropy double subspace,LEDS)的多模态过程故障检测方法,通过局部概率密度估计计算过程数据的局部熵,消除多模态特性的影响.对提取过程数据的特征信息进行Kolmogorov-Smirnov(KS)检验,分别建立高斯空间和非高斯空间的子模型,根据Bayesian融合方法将所得到的子模型的各统计量的值转化成故障发生的概率,有效地提高了多模态过程监控系统的性能.

2 基于局部熵双子空间的多模态过程故障检测

2.1 局部熵算法

熵是用来描述系统过程状态是否正常的重要统计指标.对于随机变量x,其样本集表示为x={x1,x2,···,xm},其中m是样本数.熵定义如下:

其中p(x)是变量x的概率密度函数(probability density function,PDF).为了降低传统核密度估计函数(kernel density estimation,KDE)[22–23]对窗宽参数选择的敏感度,消除数据的多模态特性,Zhong等人[21]引入一种基于kNN算法的局部学习策略,提出运用改进的局部核密度估计函数来确定p(x),其定义如下:

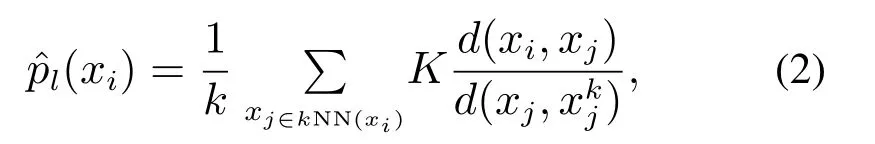
其中:xi是X的样本;kNN(xi)是xi的k近邻集,表示为

现给定一个训练数据矩阵,表示为

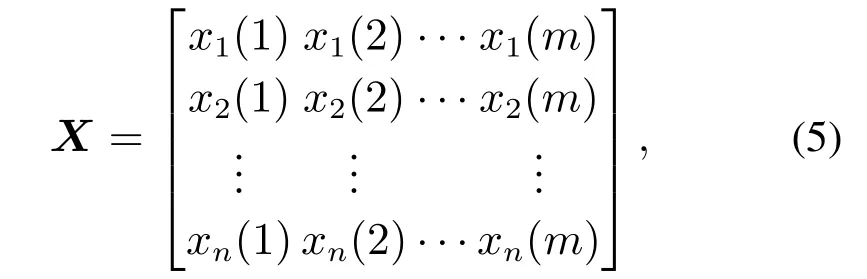
其中xi(j)表示第i个变量的第j个样本.应用熵变换提取训练数据中隐藏的固有信息.首先,利用式(2)估计每个变量的局部概率密度,得到如下的密度矩阵:

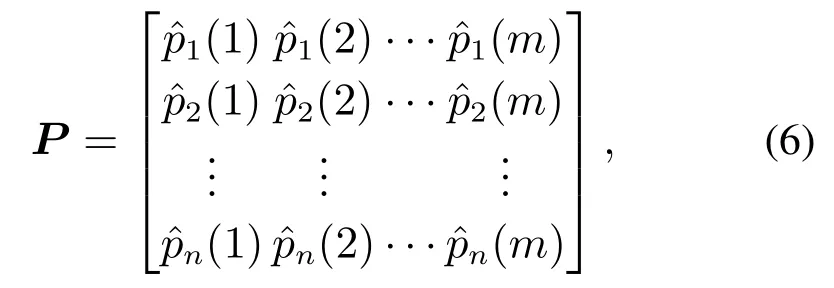
其中ˆpi(j)表示第i个变量的第j个样本的局部概率密度估计值.然后,将滑动窗口技术应用于熵变换.假设Z是滑动窗口的宽度,则数据窗口Pt定义为

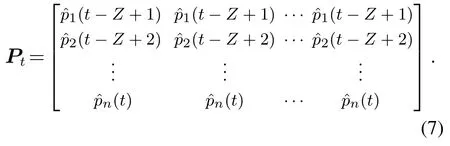
基于式(7),熵向量h计算为

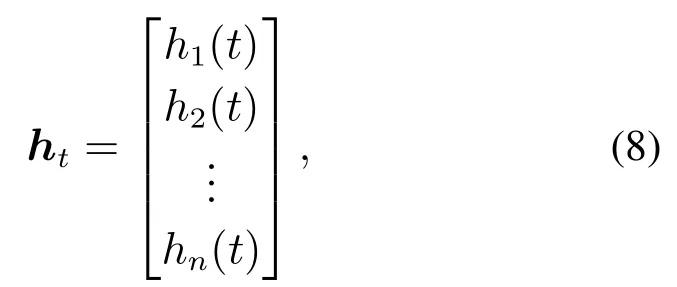
其中ht的元素定义为

利用上述方程,将数据矩阵X从原始空间转换到熵空间,得到熵矩阵

2.2 KS检验

KS检验[24]方法用来计算样本的经验分布与假设分布的拟合程度,其不需要预先知道数据的分布情况,是一种非参数检验方法.对于随机变量xt,FN表示由样本得到的经验累积分布函数,F0表示为理论累积分布函数,取|FN(xt)−F0(xt)|在随机变量上的最大值作为KS检验的统计量,则

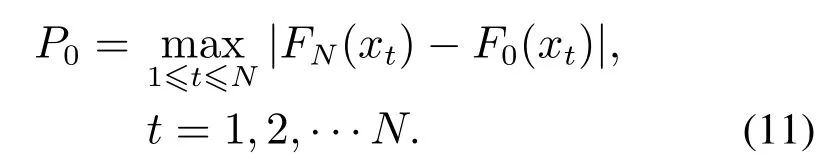
KS检验临界表得P0(n,α),其中N为变量总数,α为置信度水平,一般取0.05.原假设H0为两个数据分布一致或者数据符合理论分布,也就是说H0表示测试结果,P0为是否接受高斯分布的概率值.对于变量xt,如果H0=0且P0在5%显著性水平上,则变量xt服从高斯分布.相反,如果H0=1且P0在5%显著性水平下,则变量xt不服从高斯分布.

在局部熵变量空间中应用KS方法检验数据是否服从高斯分布,把局部熵矩阵分为高斯子空间H1和非高斯子空间H2,从而有效地提取数据变量的高斯和非高斯特征.

2.3 局部熵双子空间模型

2.3.1 局部熵高斯子空间模型

对于服从高斯分布的局部熵数据矩阵H1建立PCA模型,首先对H1进行标准化,使H1的各列方差为1,均值为0.然后计算H1的协方差矩阵如下:

其中m是样本个数.对协方差矩阵S进行特征值分解,计算出特征值和特征向量.根据累计方差贡献率[25]求主元个数v,如下:

式中λi为协方差矩阵的特征根,其中由前v个特征向量构成的矩阵就是负载矩阵Pv.根据下列公式计算Q和T2统计量:

式中Λ=diag{λ1,λ2,···,λv}.根据核密度估计确定Q和T2统计量的控制限运用PCA对服从高斯分布的局部熵数据进行监视,满足PCA要求数据服从多元高斯分布的前提假设,从而使检测结果达到预期效果.

2.3.2 局部熵非高斯子空间模型

对于服从非高斯分布的局部熵数据矩阵H2建立ICA模型.在非高斯熵变量空间中,应用FastICA提取数据的独立元.首先对非高斯局部熵数据矩阵H2进行白化,然后对H2的协方差矩阵RH2进行奇异值分解得到:

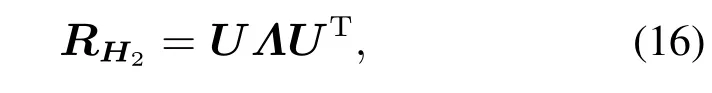
其中Λ和U为协方差矩阵RH2的特征值和特征向量.白化变换由以下公式表示:

其中O=Λ−1/2UT为白化矩阵,则有

式中W=BTO.在非高斯局部熵数据矩阵中根据式(13)确定独立元个数d.提取d个非线性独立元,并计算d个独立元的重构误差,则对于t时刻的非高斯局部熵向量ht,有

同样根据KDE确定SPE和I2统计量的控制限SPElim和以局部概率密度为基础的信息熵变换过程,消除数据的多模态差异,满足ICA关于单一模态的假设前提.

2.3.3 贝叶斯混合空间模型

在局部熵变量中分别建立PCA高斯子空间和ICA非高斯子空间模型来检测一个新来的数据集h,但是每一个子模型都会得到不同的检测结果,因此本文通过Bayesian融合方法将所得到的子模型的各统计量的值转化成故障发生的概率,以便更直接的理解故障发生的可能.具体算法如下:

其中:PQ(N),PQ(F),PT2(N)和PT2(F)分别是PCA模型残差空间和主元空间的正常和故障过程的先验概率;PSPE(N),PSPE(F),PI2(N)和PI2(F)分别是ICA模型残差空间和主元空间的正常和故障过程的先验概率.如果检验水平α被确定,则PQ(N),PT2(N),PSPE(N)和PI2(N)分别为1 −α,而PQ(F),PT2(F),PSPE(F)和PI2(F)为α.各个模型统计量是否正常的概率计算公式如下:

按上述方法将各子模型的检测结果全部转化为故障发生的概率,再利用以下公式将所有的检测结果进行组合:

新模型的统计指标ESPE和ET2控制限为1 −α,当统计量超过1 −α则系统为故障状态,否则为正常.

2.4 基于局部熵双子空间的多模态过程故障检测

LEDS方法用于多模态过程的故障检测,主要包括模型建立和故障检测两个步骤.

模型建立:

1) 收集正常运行的历史数据集X=[x1x2···xm]T∈Rm×n;

2) 标准化原始数据矩阵X得到X1;

3) 根据式(2)计算X1的局部概率密度矩阵P;

4) 根据式(8)–(10)构建对应于P 的局部熵变换矩阵H;

5) 应用KS检验对H进行子空间划分,对满足高斯分布特性的局部熵变量H1建立PCA模型,根据式(14)–(15)计算Q 和T2统计量,由KDE 确定Q 和T2统计量的控制限Qlim和.对非高斯分布的局部熵变量H2建立ICA模型,根据式(22)–(23)计算SPE和I2统计量,同样根据KDE确定SPE和I2统计量的控制限SPElim和.

故障检测:

1) 对待检测样本xnew,利用建模数据的均值和方差进行标准化得到xnew1;

2) 计算xnew1的改进局部熵得到改进局部熵矩阵h;

3) 利用KS检验将局部熵变量分为高斯子空间和非高斯子空间,然后分别向高斯子空间模型和非高斯子空间模型上投影;

4) 分别计算每个子模型的统计量Q,T2,SPE和I2;

5) 计算每个子模型两个统计量发生故障的概率;将各个子模型的检测结果进行组合,计算出ESPE和ET2;

6) 将待检测样本的ESPE和ET2与控制限1 −α进行比较,根据统计量是否超过控制限来判断样本的状态.

3 仿真结果与分析

3.1 数值仿真

以Ma设计的数值例子[26]来进行仿真,该数据中包含5个变量,模型如下：

其中e1,e2,e3,e4和e5服从[0,0.01]的白噪声.数据源s1和s2的变化可以改变操作条件,现通过改变数据源构造两种不同的操作模态.

模态1:s1∈U[−7,−4],s2∈N[−5,1];

模态2:s1∈U[2,5],s2∈N[7,1]

每个模态产生200个样本,组成具有400个样本的多模态数据集.其中每个模态的前100个样本组成训练数据集,其余样本为校验数据集.在模态1运行时,对变量x1增加幅值为0.01×(i −400)的故障,产生100个故障样本.以x1和x2为例进行说明,图1是训练样本x1和x2的变量序列图.图中横轴表示样本数,纵轴表示变量.

图1 原始数据变量序列图Fig.1 Sequence plot of training data variable

从图1可以看出,模态1的100个训练样本与模态2的100个训练样本服从不同分布,变量序列值不在同一水平线,说明该数值例子具有多模态特性.图2是将原始数据转换到局部熵空间后的变量序列图,从图2可以看出x1和x2的所有样本均在同一水平线上,说明局部熵方法把多模态数据转换为单模态.

图2 局部熵数据变量序列图Fig.2 Sequence plot of local entropy data variable

应用KS方法检验原始数据和局部熵数据变量是否服从高斯分布,结果如表1所示.对于变量xt(t=1,2,3,4,5),如果H0=0且P0在5%显著性水平上,则xt服从高斯分布.相反,如果H0=1且P0在5%显著性水平下,则xt服从非高斯分布.从表1可以看出,在原始数据中,变量x2和x4的H0为0且P0均在5%显著性水平上,则变量x2和x4服从高斯分布,说明变量x1,x3和x5具有非高斯特征;在局部熵数据矩阵中,变量x2,x3和x4服从高斯分布,变量x1和x5具有非高斯特征.

表1 KS检验结果Table 1 Results of KS test

根据KS检验提取局部熵数据的高斯变量x2,x3和x4建立PCA模型,而对非高斯变量x1和x5建立ICA模型,对每个子模型得到的不同的检测结果利用贝叶斯融合技术得到统一的统计量.使用LEDS方法对该数值例子进行故障检测,并与PCA、局部熵主成分分析(local entropy principal component analysis,LEPCA)和LEICA进行比较,检测结果如图3所示.图中:“∗”代表训练数据,“◦”代表校验数据,“”代表故障数据,虚线代表95%控制限.在PCA,LEPCA和LEICA中主成分和独立成分个数由85%累计方差贡献率确定.从图3可以看出,PCA算法的Q统计量检测出17个故障数据,13个样本出现误报;T2统计量检测出13 个故障样本,22个样本出现误报.LEPCA算法的Q统计量检测出29个故障数据,12个样本出现误报;T2统计量检测出3个故障样本,13个样本出现误报.LEICA算法的SPE统计量检测出98个故障数据,5个样本出现误报;I2统计量检测出31 个故障样本,7个样本出现误报.LEDS算法的ESPE统计量检测出全部故障数据,5个样本出现误报;ET2统计量检测出全部故障样本,3个样本出现误报.与其他3种方法相比,LEDS方法具有更好的故障检测性能.

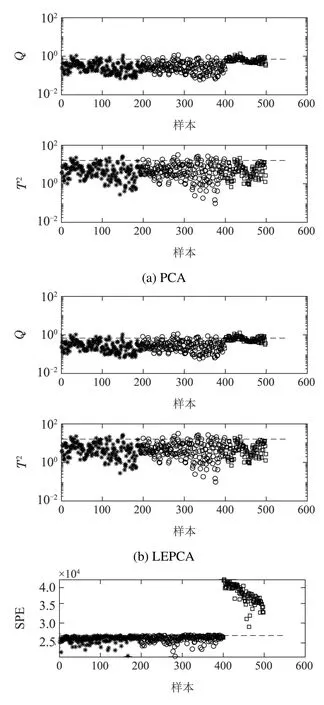
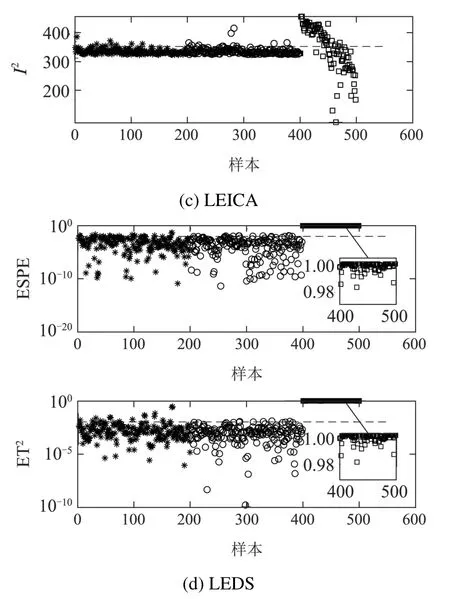
图3 4种方法对数值例子的检测结果Fig.3 Detection results of four methods for numerical example

PCA,LEPCA,LEICA和LEDS对多模态数值例子的具体检测结果对比如表2所示.表2表明LEDS在误报率较低的情况下,具有最高的故障检测率,验证了该方法在多模态数据故障检测中的有效性.

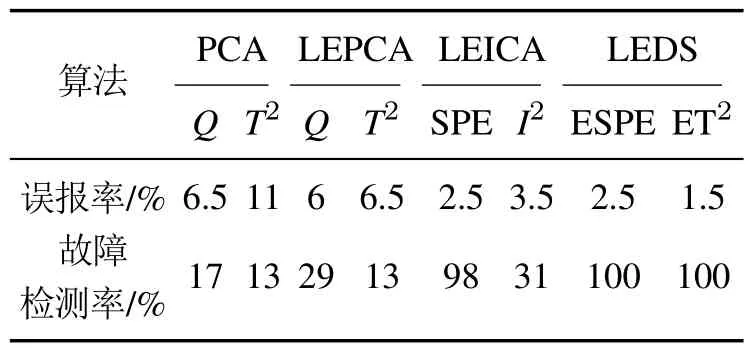
表2 4种算法对数值例子的检测结果对比Table 2 Comparisons of detection results of four algorithms for numerical example

3.2 TE多模态过程

田纳西–伊斯曼(Tennessee Esatman,TE)过程是一个模拟实际工业过程的仿真平台,国内外学者将其广泛用于故障检测与故障诊断领域,已成为一种国际上通用的标准仿真模型[27–30].TE 过程包括5个主要操作单元、4种气体进料、2个气液放热反应生成的2种主产品、2个衍生放热反应生成的2种副产品等,过程机理复杂,变量较多.TE过程具体的模型流程图如图4所示.

图4 TE过程工艺流程图Fig.4 Flow chart of TE process

选取TE过程的模态1和模态3组成具有1200个训练数据的多模态过程,并分别在模态1和模态3中选出200个正常样本作为校验数据,故障类型为模态1和模态3的故障1,2,8,9和10.在每个故障类型下选取800个样本组成测试故障数据集.在PCA和LEPCA中主成分个数以及LEICA中独立成分个数由累计方差贡献率确定.对故障10分别应用PCA,LEPCA,LEICA和LEDS的检测结果如图5所示.从图5可以看出PCA的Q统计量检测出大部分故障,但是存在误报;T2统计量故障检测率较低并且存在大量误报.这是因为PCA算法在主成分空间构造T2统计量,要求数据为单模态并且服从多元高斯分布,而TE过程的多模态数据与这一假设条件相悖,因而有较低的故障检测率.与PCA类似,LEPCA的Q统计量检测出大部分故障,但是存在大量误报;T2统计量故障检测率较低,但是检测效果优于PCA.因为LEPCA将原始数据转换到局部熵空间,消除原始数据的多模态特性,从而故障检测率有所提高.在LEICA中SPE统计量检测出大量故障,效果明显优于PCA和LEPCA,但是I2统计量故障检测效果却不十分理想.这是由于局部熵方法消除了数据的多模态特性,检测性能有所提高,但是局部熵数据中有的变量服从高斯分布,有的变量服从非高斯分布,ICA能够提取数据的非高斯特征,无法有效地提取数据的高斯特征.在LEDS方法中ESPE和ET2均能检测出大量故障,在误报较低的情况下故障检测效果优于PCA,LEPCA和LEICA,验证了LEDS算法的有效性.

TE过程4种算法的具体检测结果如表3所示.本文运用误报率和故障检测率来衡量算法的优越性,从表3可以看出,在对TE多模态过程的5种故障(1,2,8,9和10)进行检测时,与PCA,LEPCA和LEICA算法相比,LEDS在保证误报率较低的前提下故障检测率最高,验证了该算法的有效性.

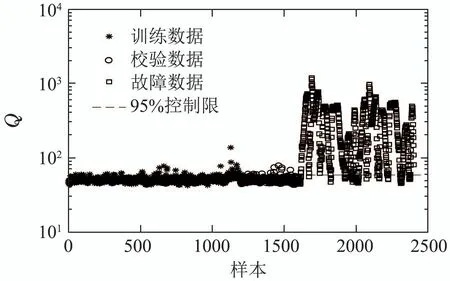
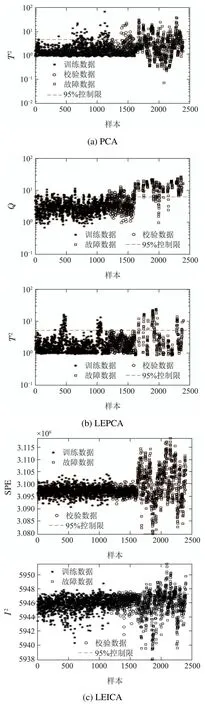
图5 故障10的检测结果Fig.5 Detection results of fault 10

表3 TE过程故障检测结果Table 3 Fault detection results of TE process

4 结论

本文提出一种基于局部熵双子空间的多模态过程故障检测方法.通过对数据的局部概率密度估计,消除多模态特性的影响.运用局部概率密度估计构造数据的局部熵信息,在局部熵空间中利用KS检验提取数据的高斯和非高斯信息,分别建立高斯和非高斯子空间模型,利用贝叶斯融合技术将各个子模型的检测结果进行融合形成统一的检测指标,进行故障检测.将本文的方法应用到数值例子和实际的TE多模态过程中,仿真结果表明,与传统的故障检测算法相比,本文算法提高故障检测率,降低误报率,验证了该方法的有效性.