含不等式约束的欠驱动系统约束跟随控制
李 旻,熊 亮,尹 辉,上官文斌,秦 武
(华南理工大学机械与汽车工程学院,广东广州 510640)
1 引言
欠驱动机械系统是指控制输入数量小于自由度数的系统[1].与全驱动机械系统相比,它通常配备更少的作动器,具有体积小、重量轻和能耗低等优点[2],因此广泛应用于移动机器人、航空航天系统、柔性系统和水下机器人等工业领域中.近年来,欠驱动机械系统逐渐成为自动控制领域比较热门的研究对象,其中有些系统甚至成为用来验证各种控制策略效果的经典案例[3–6].然而,由于欠驱动的性质,欠驱动系统往往表现出复杂的内部动力学特性,给其控制研究带来很大困难.目前,很多学者将线性二次型调节器(linear quadratic regulator,LQR)控制[7–8]、滑模控制[9–10]、模糊控制[11–13]和反推演示控制[14–15]等传统控制方法应用于各式欠驱动系统复杂控制问题.Bullo等提出了欠驱动系统的位移和速度控制方法[16];Pettersen等研究了欠驱动车辆系统轨迹跟踪和避障等多目标控制方法[17–20];Azeloglu和Smoczek等提出了欠驱动起重机系统的自适应模糊逻辑控制器[21]和基于粒子群优化的广义预测控制[22];Sun 等提出了含不确定参数和双摆摆动效应的欠驱动起重机系统非线性稳定控制方法[23–24].
Chen将Udwadia-Kalaba(U–K)方 程[25–26]成 功 引入到需满足一系列等式约束(包括完整和不完整约束)的全驱动机械系统,并首次提出了基于U–K方程的状态反馈约束跟随控制方法[27–29].该方法的基本思想是将系统控制目标(系统镇定、轨迹跟踪和最优控制等)设计成一系列的约束(约束数量与自由度数量可不相同),控制任务即是驱动系统满足这些约束(因此为约束跟随控制).相较于其他控制方法,该方法不需要对非线性系统进行线性化,且可在不出现任何辅助变量(如拉格朗日乘子)或伪变量(如广义速度)的情况下得到系统状态反馈控制律的显式方程,此外,所得的控制力满足高斯最小原理和达朗伯原理的拉格朗日形式,实际过程中会提供适度的控制.近年来,基于U–K的约束跟随控制在全驱动不确定系统中得到了广泛的研究和应用.然而,基于U–K方程的约束跟随控制不适用于欠驱动系统.Yin等[30]进一步地将约束跟随控制方法扩展到含有等式约束的欠驱动系统,实现了欠驱动二轮式移动机器人系统的轨迹跟踪控制.但是,利用约束跟随控制方法处理含有不等式约束的欠驱动系统,目前尚未见到相关报道.
平面垂直起降(planar vertical take-off and landing,PVTOL)飞行器是一种典型的非线性强耦合欠驱动系统.由于空气弹性效应、机翼的柔韧性、发动机的内部动力学以及众多变量的影响,该系统的整个动力学相当复杂.Hauser等[31]简化了飞行器的结构,只保留设计控制律时必须考虑的主要特征,将PVTOL飞行器假设成一个三自由度的的欠驱动系统,该系统模型已成为欠驱动系统的一个经典案例[6],并被广泛应用于验证各种控制方法的控制效果[32–36].文献[37–38]通过近似输入–输出线性化方法来研究该系统的稳定性、位置控制以及输出跟踪问题,但在设计控制器时都忽略了滚动力矩和横向加速度之间的耦合,而实际中这种耦合是不可忽略的.PVTOL飞行器在运动过程中常需要按照操纵者的意图进行轨迹跟踪和姿态保持控制,且在收敛到目标轨迹或姿态的过程中需要服从一定的边界限制.例如,由于自身结构设计、功率及外部因素限制,飞行器运动时存在最大飞行高度,机翼存在最大摆角,而现有的研究中大多没有考虑边界限制[39–41].
在上述研究基础上,本文提出了含不等式约束的欠驱动系统约束跟随控制方法.首先,只考虑系统需要满足的等式约束(完整或不完整约束),运用约束跟随控制方法推导出基于系统模型的状态反馈伺服控制律;其次,考虑系统需要满足的不等式约束,先通过状态变量映射将不等式约束整合到原等式约束中以得到新的等式约束,再基于新的等式约束、新的系统模型和第一步中的约束跟随控制方法,推导出系统所需的状态反馈伺服控制律;最后,将该约束跟随控制方法应用于三自由度非线性强耦合的PVTOL飞行器以验证其控制效果.将PVTOL飞行器的轨迹跟踪和姿态保持表示成等式约束,将飞行器质心在垂直方向上的高度限制表示成不等式约束.仿真结果验证了该方法的有效性.此外,本文将该方法与现有的全驱动系统约束跟随控制方法和LQR控制方法进行了对比,仿真结果表明该方法在处理诸如PVTOL飞行器等非线性强耦合的欠驱动系统控制问题时具有一定的优越性.最后,为进一步突出该方法的适用范围,本文假设了一种等式约束(含完整和非完整约束)和不等式约束(含单边和双边不等式)同时存在的情况,仿真结果表明该方法也可处理这类复杂问题.
2 处理等式约束的欠驱动系统约束跟随控制
2.1 系统描述
欠驱动机械系统动力学模型可表述为

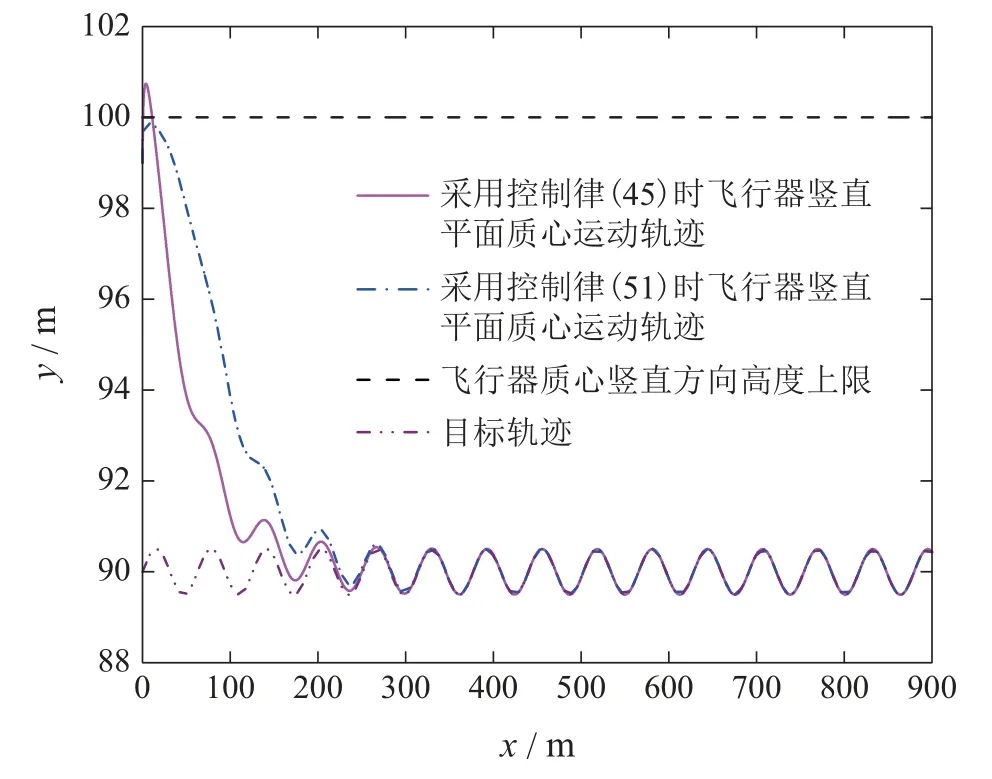
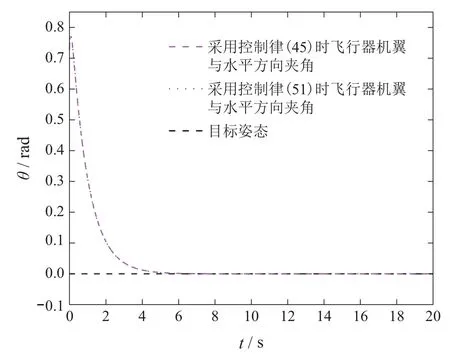
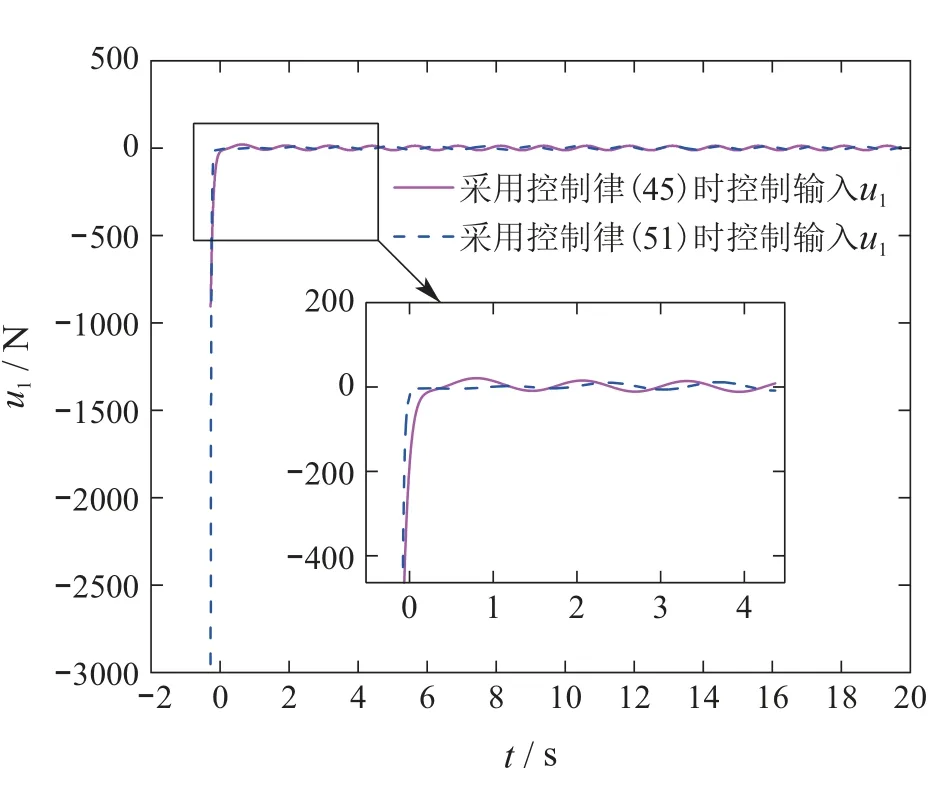
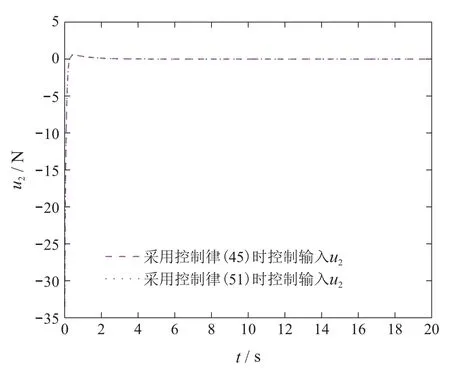
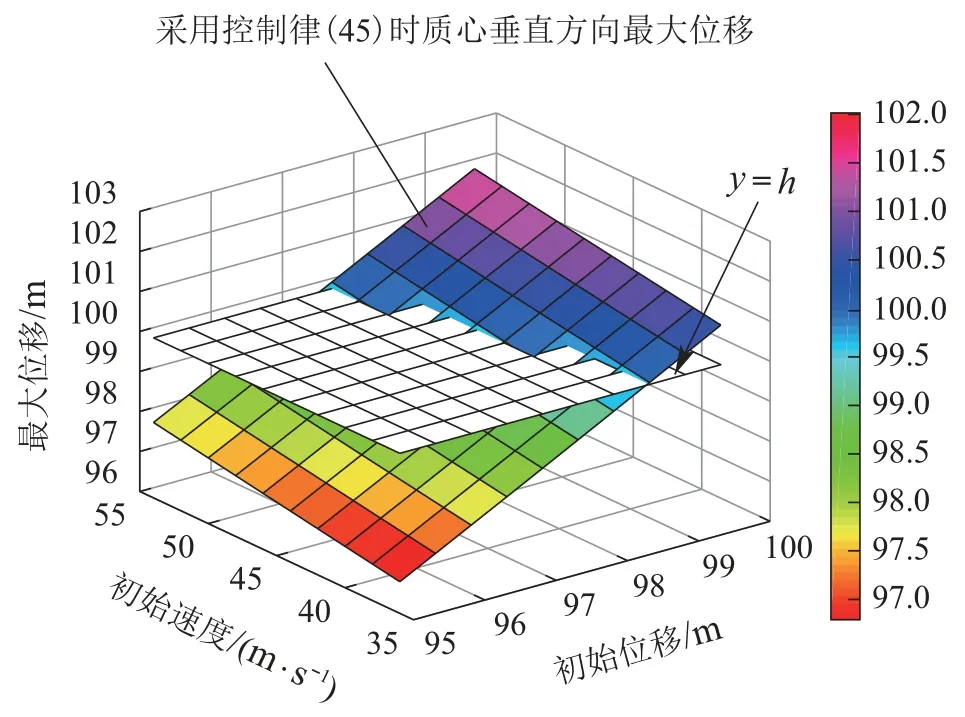
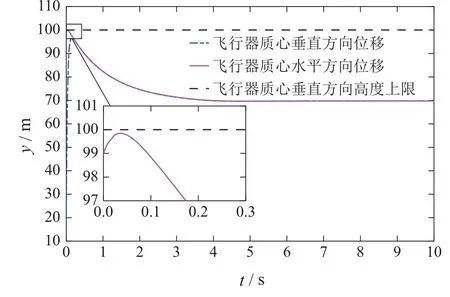
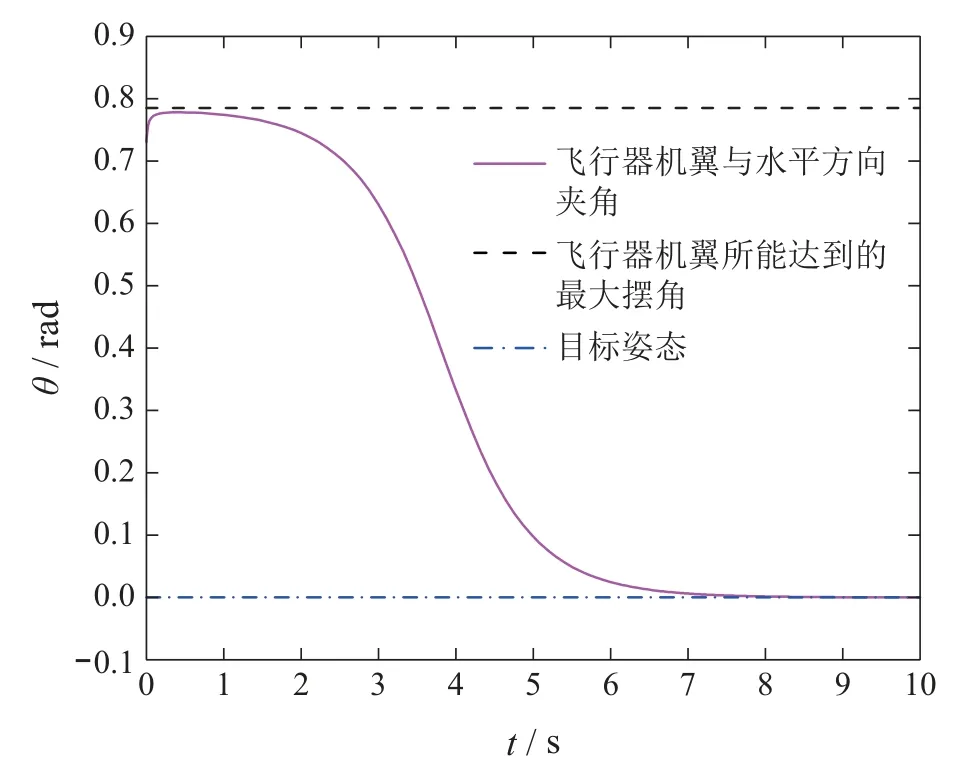
其中:t ∈R为运动时间;q ∈Rn为系统的位置矢量;n 为系统的自由度数;∈Rn为系统的速度矢量;∈Rn为系统的加速度矢量;τ ∈Rm(m 假设系统需要满足m个连续可微的等式约束,包括完整约束或非完整约束,以下对这两种情形分别进行讨论. 情形1等式约束是完整的,即约束方程中不包含坐标对时间的导数,或者约束方程中微分项可以积分为有限形式,如下所示: 其中:t ∈R为时间,q ∈Rn为系统的位置矢量,约束(2)等效为 其中:φi,µi为正常数,i=1,2,···,m. 注1将ψi(q,t)作为一个整体,则式(3)是一个二阶常系数齐次线性微分方程,当系数都为正的常数时,该方程的解随着时间的增加必趋近于0.即在控制输入的作用下,如果系统满足式(3),则系统最终可渐进收敛到约束(2),从而满足相应的控制目标.值得提出的是,若将式(3)展开,则该方程可能是非线性的. 情形2等式约束是非完整的,即约束方程包含坐标对时间的导数,且微分项不利用动力学方程无法直接积分,如下所示: 注2将ψi(q,,t)作为一个整体,则式(9)是一个一阶常系数齐次线性微分方程,当系数为正的常数时,该方程的解随着时间的增加必趋近于0.即在控制输入的作用下,如果系统满足式(9),则系统最终可渐进收敛到约束(8),从而满足相应的控制目标.值得提出的是,若将式(9)展开,则该方程是非线性的. 定义1对于给定的矩阵A和b,如果方程(13)至少存在一个解,则称约束(13)是一致的. 引理1根据文献[42],约束(13)一致的充要条件是AA+b=b,其中A+表示A 的Moore-Penrose广义逆矩阵. 假设1约束(13)是一致的. 注3假设1保证了约束(13)是实际可行的.式(13)是一个通用的等式约束形式,其既可以表示完整和非完整约束,也可以表示文献[43–44]中的目标约束.此外,文献[27]中的控制目标(包括轨迹跟踪、系统镇定和最优控制等)都可以先设计成相应的约束,再通过求导转换成约束(13)的形式.因此,约束(13)可以涵盖实际工程中大多数的控制目标. 注4将含n个自由度系统的镇定、轨迹跟踪等控制目标设计成相应的等式约束时,约束数量不一定与自由度数相同[45–47],视具体情况而定即可. 对于给定的形如式(1)的欠驱动系统以及相应的系统所需满足的等式约束(13),控制律的求解主要按照以下两个步骤进行: 以上过程称为处理等式约束的欠驱动系统约束跟随控制方法. 如第2.3节所述的约束跟随控制方法成功解决了欠驱动系统在等式约束下的控制输入求解问题,但当系统同时存在不等式约束时,该方法可能无法满足要求.为同时处理含等式和不等式约束的欠驱动系统,需要先通过状态变量映射将不等式约束整合到原等式约束中以得到新的等式约束,再基于新的等式约束、新的系统模型和第2.3节所述的约束跟随控制方法,推导出系统所需的状态反馈伺服控制律.将该控制律加入到原系统中,即可使原系统既满足等式约束要求又满足不等式约束要求. 欠驱动机械系统(1)在运动过程中常需要服从一系列的不等式约束,包括双边和单边不等式约束,如下所示: 其中:t ∈R为时间,q ∈Rn为系统的位置矢量,cj为常数,l(lm)为总的不等式约束数量,L(Ll)为双边不等式约束的数量. 现在假设系统需要同时满足如式(13)所需的m(m 步骤1对于不等式约束(22)–(23),定义状态变量映射如下: 其中R=(−∞,+∞).即通过状态变量映射Ti,Tj可将原含有不等约束的状态变量空间映射到无不等式约束的新状态变量空间,此时新的状态变量zi,zj就没有不等式约束限制了.由于新空间的状态矢量=[z1z2··· zl]T的维数l可能少于原空间状态矢量q的维数n,所以需要再添加n −l个独立变量构成新空间n维的状态矢量z=[z1z2··· zlzl+1··· zn]T,其中zl+1··· zn都是关于q的函数.再根据式(24)–(25)可推导出z与q的关系为 步骤2由步骤1得到新的系统动力学方程(33)及其需要满足的等式约束(31),根据第2.3节所述处理等式约束的欠驱动系统约束跟随控制方法,可得系统新的的控制输入为 以上过程称为含不等式约束的欠驱动系统约束跟随控制方法. 注5处理含不等式约束的欠驱动系统控制问题时采用的是倒推的方法.先假设不等式约束满足,通过状态变量映射(24)–(25)得到新的无不等式约束系统模型(即系统动力学方程(33))以及新的等式约束(31),再运用第2.3节所述的约束跟随控制方法求解相应新的控制输入.将此控制输入代入到原系统中即可使原系统同时满足等式和不等式约束. 综合第3.1节和第3.2节所述,处理欠驱动系统的约束跟随控制方法主要流程如图1所示. 图1 欠驱动系统约束跟随控制方法设计过程Fig.1 Control design procedure for the underactuated systems 如图2所示为PVTOL飞行器运动简图.系统的归一化动力学方程[31]为 该系统是一个双控制输入的三自由度欠驱动系统.其中x,y分别表示飞行器质心的水平与垂直位移,θ为机翼与水平方向的旋转夹角,为相应的加速度.控制输入u1是飞行器底部垂直于机翼的推力,控制输入u2是使飞行器旋转的转动力矩.“−1”表示归一化后的重力加速度,ε是转动力矩与横向加速度之间的耦合系数.将系统(36)写成式(1)的矩阵形式为 则式(1)中M,C,G,B,τ可分别表示如下: 图2 平面垂直起降(PVTOL)飞行器Fig.2 Planar vertical take-off and landing(PVTOL)aircraft PVTOL飞行器运动时经常需要进行轨迹跟踪和姿态保持控制,因此需要满足相应的等式约束.为验证本文约束跟随控制方法,将控制目标设计成以下的等式约束形式: 其中µ,ω,H,β都为常数. 定义跟踪误差: 定义误差函数: 其中收敛系数κ1,κ2,ρ1,ρ2都为正的常数.若要系统跟踪目标轨迹和目标姿态,即当t →∞时,跟踪误差e →0.则由式(3)可知系统需满足如下等效的等式约束: 将式(40)–(41)代入上式并写成式(13)统一的等式约束矩阵形式,则A和b可表示为 显然矩阵A 是行满秩的,所以根据第2.2 节引理1 有AA+b=(ATA)−1ATAb=b,假设1成立.且由式(17)得 显然rank[Φ1Φ2]=21,故假设2成立,该系统是伺服约束可控的.于是由式(18)并令S=0可得系统的状态反馈伺服控制律为 实际情况中,PVTOL飞行器由于自身结构设计、功率及外部因素限制,飞行器运动时存在最大飞行高度.由第4.2节所述,在式(45)的控制输入下,飞行器最终会满足等式约束(39)从而按照期望的轨迹和姿态运动.但满足目标约束前会有一个收敛的过程.由于飞行器的初始状态是未知的,如果初始条件比较恶劣,飞行器收敛到目标轨迹的过程中很可能会超出边界限制,此时控制律(45)可能无法满足控制要求.因此,除等式约束(40)外,考虑如下的不等式约束: 其中h为飞行器质心在垂直方向能达到的最大高度.根据式(25),定义如下状态变量映射: 显然z1∈R.将原系统状态矢量q=[x y θ]T变换为新的状态矢量z=[x z1θ]T,此时新的状态空间就没有不等式约束限制了.将式(47)代入式(36)得新的系统动力学方程 写成式(33)所示的矩阵形式,可得 将式(47)代入式(39)可得新的等式约束 重复第4.2节步骤,由式(35)并令S=0可得系统的状态反馈伺服控制律为 其中: 参照第3–4节所述,设PVTOL飞行器系统的初始值为x(0)=0,(0)=10 m/s,y(0)=99 m,(0)=40 m/s,θ(0)=0.73 rad,(0)=1.5 rad/s.系统相应的参数如表1所示. 表1 PVTOL飞行器系统参数Table 1 The system parameters of PVTOL aircraft 考虑系统需满足的等式约束(39)与不等式约束(46),分别采用控制律(45)(51),仿真结果如图3–6所示. 图3为PVTOL飞行器质心在竖直平面上的运动轨迹;图4为PVTOL飞行器运动过程中机翼与水平方向夹角;图5和图6分别为控制输入u1和u2.仿真结果表明: a) 系统在控制律(45)的作用下,飞行器质心在竖直平面上的运动轨迹最终收敛于目标轨迹,飞行器机翼最终保持目标姿态(机翼与水平方向夹角为0),满足等式约束(39)要求.所以处理等式约束的欠驱动系统约束跟随状态反馈控制律(45)是有效的.但飞行器质心在垂直方向上的最大位移会超过最大高度限制y=100 m. b) 系统在控制律(51)的作用下,飞行器质心在竖直平面上的运动轨迹最终收敛于目标轨迹,飞行器机翼最终保持目标姿态(机翼与水平方向夹角为0),且飞行器质心垂直方向最大高度不超过最大高度限制y=100 m,同时满足等式约束(39)和不等式约束(46)要求.所以,处理含不等式约束的欠驱动系统约束跟随状态反馈控制律(51)是有效的. c) 图5表明,若要飞行器质心在垂直方向的位移不超过最大高度(考虑不等式约束),则系统控制输入需要相应的增大,控制成本相对提高,这也符合实际情况. 为进一步比较系统考虑不等式约束前后飞行器运动表现的差异,本文还设置了一系列的初始条件组合,通过仿真得到每组初始条件下飞行器质心在垂直方向的最大位移,如图7所示. 显然,由图7 可知只考虑等式约束,采用控制律(45)时,在部分初始条件组合下,飞行器质心垂直方向最大位移将超过最大的允许高度100 m;由图8可知当考虑等式和不等式约束,采用控制律(51)时,无论何种初始条件组合,飞行器质心垂直方向最大位移均小于最大的允许高度y=100 m. 图3 PVTOL飞行器质心在竖直平面上的运动轨迹Fig.3 Trajectory of the center of mass of PVTOL aircraft in the vertical plane 图4 PVTOL飞行器机翼与水平方向夹角Fig.4 PVTOL aircraft wing Angle with the horizontal direction in the time history 图5 控制输入u1Fig.5 The control input u1 in the time history 图6 控制输入u2Fig.6 The control input u2 in the time history 图7 只考虑等式约束,采用控制律(45)时飞行器质心垂直方向最大位移Fig.7 Maximal vertical displacement y of the center of mass of PVTOL aircraft in the time history under the control obtained by(45)which only considering equality constraints 图8 考虑不等式约束,采用控制律(51)时飞行器质心垂直方向最大位移Fig.8 Maximal vertical displacement y of the center of mass of PVTOL aircraft in the time history under the control obtained by(51)which considering inequality constraint 此外,为比较不同控制方法对PVTOL飞行器控制效果的差异,本文将关于欠驱动系统的约束跟随控制方法与基于U–K方程的全驱动系统约束跟随控制方法[27–28]和LQR方法[7–8]对比如图9–10所示. 显然,由图9可知,基于U–K方程的全驱动系统约束跟随控制方法并不能解决欠驱动PVTOL飞行器系统的轨迹跟踪问题,而本文提到的欠驱动系统约束跟随控制方法能实现PVTOL飞行器的轨迹跟踪;由图10可知,传统的LQR控制方法无法解决非线性PVTOL 飞行器系统的姿态保持问题,而本文提到的欠驱动系统约束跟随控制方法能实现PVTOL飞行器的姿态保持. 图9 欠驱动与全驱动系统的约束跟随控制方法比较Fig.9 Comparison between constraint-following control for underactuated systems and fullactuated systems 图10 欠驱动系统约束跟随控制方法与LQR控制方法比较Fig.10 Comparison between constraint-following control for underactuated systems and LQR control 第5.1节所述的仿真案例表明本文提出的欠驱动系统约束跟随控制方法能够同时处理式(39)所示的完整等式约束(轨迹跟踪和姿态保持)和式(46)所示的单边不等式约束(边界服从),具有一定的现实应用意义.为进一步丰富该方法的适用范围,如下举出一例同时含有等式约束(包含完整和非完整约束)和不等式约束(包含单边和双边不等式约束)的案例: 参照前文所述,设PVTOL飞行器系统初始条件为 仿真结果如图11–14所示.仿真结果表明: 相对于以往针对欠驱动系统的控制方法大多只处理了系统所涉及的完整等式约束问题,文本所提出的含不等式约束的欠驱动系统约束跟随控制方法能够同时处理含有等式约束(包含完整和非完整约束)和不等式约束(包含单边和双边不等式约束)等较为复杂的情况,具有较强的适用性. 图11 只考虑等式约束(53),PVTOL飞行器质心竖直方向位移Fig.11 Vertical displacement y of the center of mass of PVTOL aircraft in the time history by only considering equality constraits(53) 图12 只考虑等式约束(53),PVTOL飞行器机翼与水平方向夹角Fig.12 PVTOL aircraft wing Angle with the horizontal direction in the time history by only considering equality constraits(53) 图13 同时考虑约束(53)–(54),PVTOL飞行器质心竖直方向位移Fig.13 Vertical displacement y of the center of mass of PVTOL aircraft in the time history by considering constraits(53)–(54) 图14 同时考虑约束(53)–(54),PVTOL飞行器机翼与水平方向夹角Fig.14 PVTOL aircraft wing Angle with the horizontal direction in the time history by considering constraits(53)–(54) 对欠驱动机械系统的控制一直是控制领域比较棘手的难题.本文在相关研究基础上提出了一种含不等式约束的欠驱动系统约束跟随控制方法,该控制方法既能保证系统的性能表现又满足相应的安全需求.本文的主要内容可总结为如下几点: 1) 针对控制领域比较棘手的欠驱动系统运动控制问题,本文提出了一种新颖的解决方法.该方法将基于等式约束的欠驱动系统约束跟随控制与状态变量映射方法相结合,可同时处理含等式约束(完整和非完整约束)和不等式约束(单边和双边不等式约束)的欠驱动系统,且不需要对非线性系统进行线性化,可在不出现任何辅助变量(如拉格朗日乘子)或伪变量(如广义速度)的情况下得到系统状态反馈控制律的显式方程. 2) 将该约束跟随控制方法成功应用于三自由度非线性强耦合的欠驱动PVTOL飞行器运动控制上.首先,将飞行器的轨迹跟踪和姿态保持表示成等式约束,将飞行器质心在垂直方向上的高度限制表示成不等式约束;其次,运用约束跟随控制方法求解出飞行器在等式约束下的控制律,仿真结果表明该控制律满足要求;最后,运用状态变量映射方法将不等式约束整合到原等式约束中得到新的等式约束和新的系统模型,即可将含有不等式约束的状态空间变换到无不等式约束空间,再次运用约束跟随控制求出系统的控制律.仿真结果表明该控制律可以使PVTOL飞行器同时满足轨迹跟踪、姿态保持和边界限制的要求. 3) 将本文所提的含不等式约束的欠驱动系统约束跟随控制方法分别与基于U–K方程的全驱动系统约束跟随控制方法以及传统的LQR控制方法相比较.仿真结果表明,基于U–K方程的全驱动系统约束跟随控制方法并不能实现欠驱动PVTOL飞行器系统的轨迹跟踪,传统的LQR控制方法也无法实现非线性强耦合PVTOL飞行器系统的姿态保持.而本文所提的欠驱动系统约束跟随控制方法能够处理诸如PVTOL飞行器等非线性强耦合欠驱动系统的控制问题,且能够同时处理等式与不等式约束,从而证明了该方法具有一定的优越性.2.2 等式约束






2.3 处理等式约束的欠驱动系统约束跟随控制


3 含不等式约束的欠驱动系统约束跟随控制
3.1 不等式约束

3.2 含不等式约束的欠驱动系统约束跟随控制


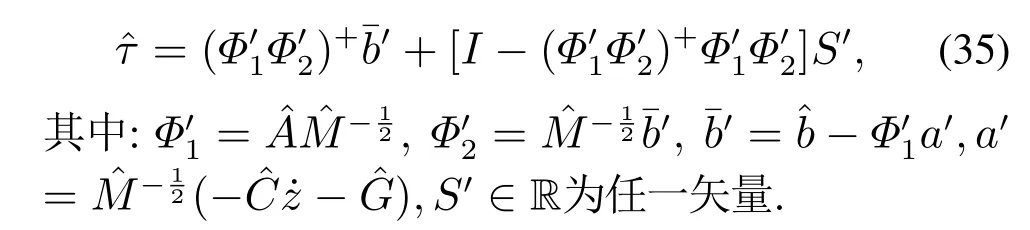

4 基于约束跟随的PVTOL飞行器运动控制
4.1 欠驱动PVTOL飞行器动力学模型
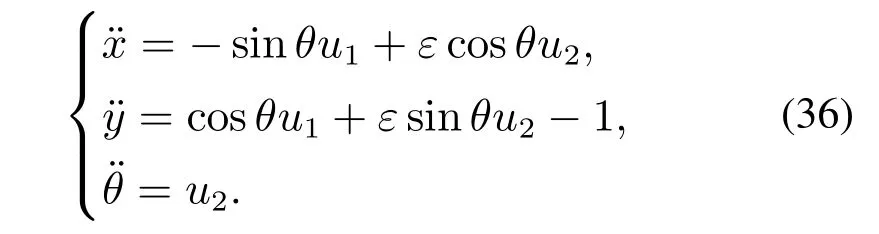



4.2 只 含 等式 约束(轨 迹跟 踪、姿 态保 持)时系 统控制律求解

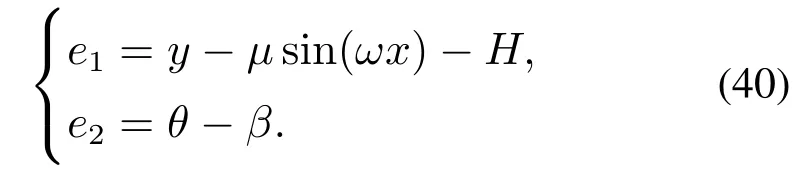




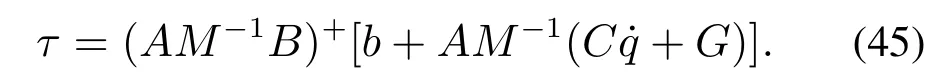
4.3 含不等式约束(边界服从)时系统控制律求解


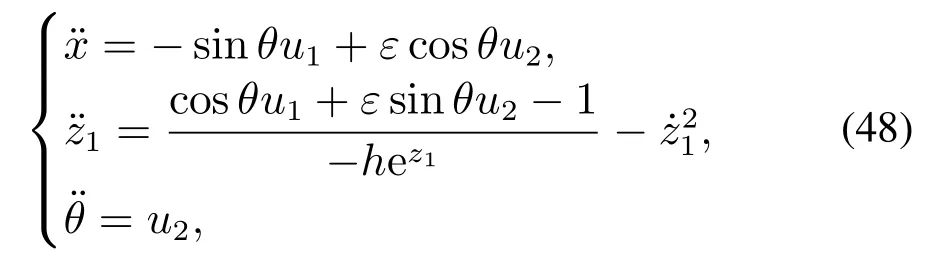
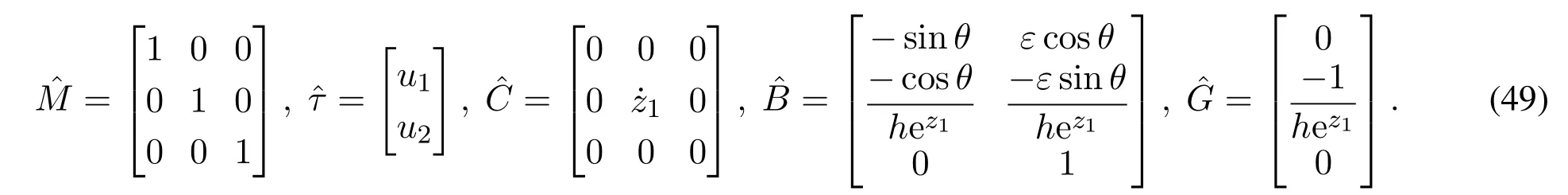


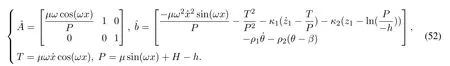
5 欠驱动PVTOL飞行器运动仿真结果
5.1 仿真案例1
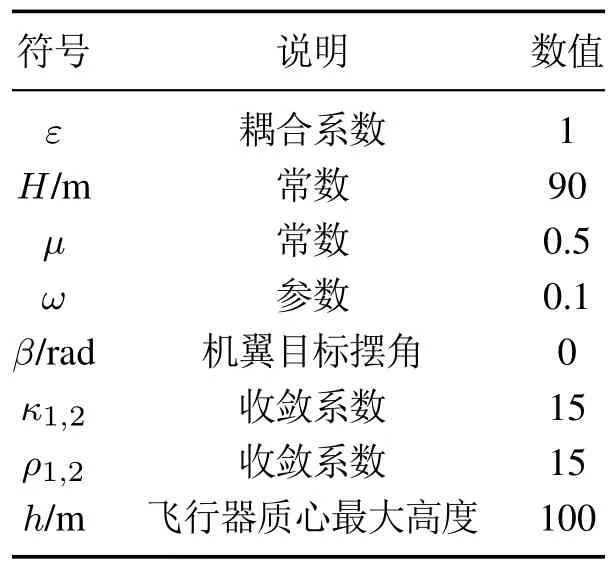



5.2 仿真案例2




6 结论

