习题设计的SLD路径
□叶蓓
教师在拓展习题时常常会以学生处理信息、表征思路为能力要求。编制这类习题,采用SLD路径是一个方向。
SLD是指“筛选(Select)素材→联结(Link)学力→描述(Describe)过程”。教师选择的习题素材,要有利于在学生答题后,教师容易明晰其解题思路,即思维显性化;学生答题也要遵循SLD的要求,对题干信息进行识别(S)→关联(L)→数学描述(D)。SLD不同于通常只关注习题解答结果的教学,而是偏重学生信息处理和表征能力的提升。
一、Select:基于教材资源
教师在进行SLD设计时,需创设信息环境,即精心检索和处理编题素材,使学生展现“信息发现、信息构建、信息输出”的思维过程,有效表征解题过程。
(一)整合
教师根据不同的数学板块知识,根据单元、学段知识选择素材。教师还可以在学科间跨界选择素材,或在现实生活中选择时事资源。例如人教版四年级上册“大数的认识”,教材主要以省市人口总数为简单信息,教师可以将其与该学期的“公顷和平方千米”“统计”等单元及四年级下册的小数单元整合,检索以阅读信息为主的习题素材。可以以杭州亚运会为背景,选择杭州城市比赛场馆、地铁里程等信息为素材,结合“公顷和平方千米”单元,选择相关人口(性别、老龄化……)、生态(植被、水域……)、社会(行业、就业……)等素材,让学生通过多文本阅读,完成相关计算(如图1)。这既能匹配知识点的教学,又能丰富学生的认知。
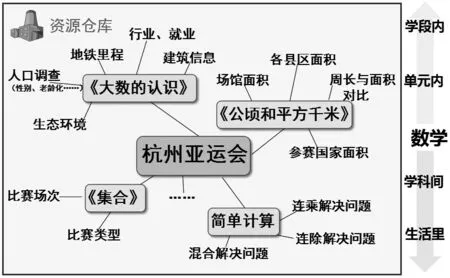
图1 四上以“亚运会”为背景的素材选择
(二)融合
素材选择除了匹配教材知识点外,还要适合开发,将素材的价值与学生的兴趣有效融合,编制智趣、实用的习题。
图2 是以乘法估算为对象选择的素材,将常规的一个数接近整十数设计成两个因数都接近整十数的算式,学生可以使用多种方法来估算。所选素材注重激发学生的探索需求,学生能够尝试用多种方法来解决问题,满足不同学习程度学生的需求,并且可以找到该算式在生活中的应用。

图2 三上“多位数乘一位数”估算的素材检索举例
选择素材还要关注素材的“可操作性”,能够借素材来激活“估算、说理、作图、列式”等多元的操作。例如本题28×9,根据估算方式的不同,选择合理的情境,进行充分说理,通过由式到文的编题,学生可体验正向思考和逆向思考的过程。
(三)挖掘
对教材存在的“习题盲区”,教师可通过对教材的精细分析,选择有关素材,使得知识在“无中生有”中变厚、增强。例如人教版四年级下册“平均数和条形统计图”单元中的平均数知识,教材仅安排了两个例题来教学平均数的意义和求平均数的基本方法。这对于学生认识平均数和求平均数的变式题是不够的。因此教师可以选择有关平均数的生活场景为素材。
教师也可以改编常见的素材背景,重设情境,从知识的考查转向能力的考查。如教学“平均数”,“总数÷份数=平均数”是正向解决问题,而根据平均数求份数或者总数的逆向问题,教材并没有安排类似习题。因此教师可以将教材习题变式,让学生全方位感受平均数概念以及求平均数的方法,如图3所示,先补充关于平均数的估算,提升学生对平均数作为总体量的集中趋势的感悟;再通过“已知平均数,求其中个别数”的两种逆向方法,让学生体验变式;最后以平均数结合条形统计图,填补教材的习题盲点,增加学生对该知识点的感悟。

图3 四下“平均数”挖掘隐形知识举例
二、Link:信息联结
教师选择的信息素材,不仅需要考虑呈现的方式、位置等,还要关注各个信息之间的层级联系,以考查学生阅读信息、分析信息、构建信息的能力。
(一)平衡
辨别题中的无关信息是学生信息处理时的弱项,教师在对素材进行精加工时,需考虑信息的呈现方式。在设计习题时,教师可以根据问题情境平衡两类信息占比,以便从学生的答题情况看出学生信息筛选的能力,如图4所示,有效信息和干扰信息的比例较为合理,学生在求“羽毛球总价”时需选择合适的信息。

图4 四下“四则运算”信息处理方式举例
教师还要关注有效信息和干扰信息出现的位置,有效信息和干扰信息不独立呈现,两者融为整体自然呈现,有效信息和干扰信息均在文本里和图里出现,综合考查学生读题的完整性和全面性。
(二)合理
习题信息的呈现方式会影响学生对信息的构建,教师在设计习题时,要关注信息以图、文、表等何种方式呈现。如图5所示,信息可以以对话形式呈现,也可以将信息以表格、图文等方式呈现。信息的不同呈现方式,可以量化调查学生的答题情况,从而了解学生对信息读取和理解的程度。

图5 习题中信息呈现的若干种方式
此外,还要关注信息之间存在着的关联级数。学生对信息的跨层联系,往往理解不当。如四下的乘法运算定律,例题用了较复杂的植树信息:“一共有25个小组,每组里4人负责挖坑、种树,2人负责抬水、浇树。每组要种5棵树,每棵树要浇2桶水……”学生对信息进行分层处理的能力较弱,表现在解决“一共要浇多少桶水”时,对于算式25×2×5的第一步25×2,缺少正确解释。因此教师在设计习题时,可以充分考虑信息之间不同层级的联系,小学中段以两层联系为主,提升学生优构信息的能力。
(三)有效
编制习题时要考虑评价:所选素材是否能有效地量化评价学生的学习能力。教师在选择素材时,要关注该素材是否能被不同层次的学生所理解,过于专业化、学科化的知识可能会让部分学生产生理解障碍,因此所选信息要面向全体学生。如图6的营养午餐个性化定制方案,素材来源于校园午餐的配餐数据调查,贴近全体学生的生活现实,他们可以根据题目要求,获得多种解题方案。
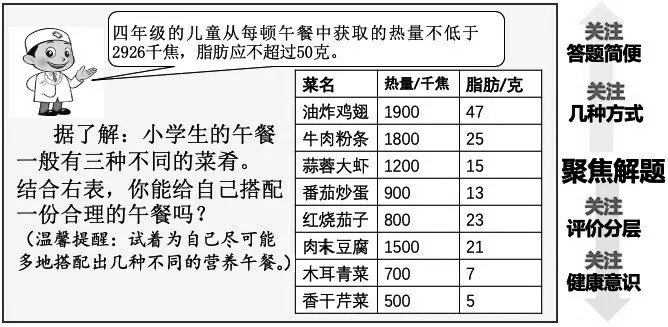
图6 四下“营养午餐”个性化定制方案举例
教师还要考虑学生的能力差异,选择的素材通过学生答题可以有效评价学生思维的层级水平,为教师有的放矢地进行差异化辅导提供依据。如上题,根据学生选择午餐方案的合理与否:他们是凑出来的,还是通过先确定较小数据再精准搭配的,按数量给予对应的评价。
三、Describe:设计表达
教师在精选素材后,要关注问题提出的方式,使问题解答成为学生思维外显的载体。
(一)递升
由于对学生表达能力的训练偏少,所以教师要在考虑学生个体差异的基础上,设计递升式问题,以适应学生的能力水平。例如可以先给予“拐杖”进行模仿,即架构好表述的框架供学生模仿学习。
在一题多问的设计架构中,通过设计梯度问题,将模仿学习递升为独立操作,如图7是三年级上册关于加减法的估算问题。学生对估算的生活体验不多,此题不同于前面的举例,它先给予学生思维的拐杖,引导学生从估算的角度去思考问题,再将任务分层推进,让思维依阶而行。

图7 三上“万以内数的加减法”估算解题框架举例
(二)全面
习题的设计还可以将提问形式从条件到问题逆转成从问题到条件,考查学生的表达形式可算式、可说理、可画图等。例如图8举例的36÷6,将算理理解与文本阅读结合,将画图作为文本阅读后理解算理的表征形式,从算法提升到算理,培养学生的推理能力。
在同一题中,还可以设计多种综合提问,如在常规的解决问题过程中,设计填空、选择、判断等不同提问方式,以考查学生信息的构建、策略的选择等能力。例如图8,即将单一的口算模式变成多种形式进行考查,有作图、选择等,以全面了解学生对于该知识点的掌握程度。

图8 三下“除数是一位数除法”多维提问举例
(三)丰盈
训练思维可以以不同题型为载体,可以设计自学型、开放型、半开放型、提问型、证明型、说理型等数学问题模型,丰富学生自学、推理、说理、验证、反思、创新等多种数学体验,如图9所示。几何问题,常涉及辅助线的添加,平时的几何教学对添加辅助线缺少指导,图9原题是人教版三下的内容,教材已经标好辅助线。教师在编制习题时,不妨去掉辅助线,增加说理、证明、反思等答题形式,帮助学生通过主动添加辅助线而形成解题模式。

图9 “长方形的周长和面积”的数学体验举例
SLD习题编制改变了教师常规设计习题的现状,倡导教师从知识与技能、过程与方法和情感与态度价值观方面设计习题,注重学生答题思维的有序和外显,培养学生综合分析和逻辑解答的能力。

