探循环之“源理”定循环之依据
——以学定教“循环小数”实录与评析
□于飞执 教曹明 徐丹红评析
【教学内容】人教版五年级上册第33-34页。
【教学目标】
1.认识循环小数,理解循环小数产生的原因,并能正确使用循环小数表示商。
2.通过自学交流、计算验证等学习活动,培养学生质疑探究、发现问题和提出问题的能力。
【教学重点】认识循环小数,理解循环小数产生的原因。
【教学过程】
一、直接揭题,获取学情
师:今天学习“循环小数”(板书:循环小数)。你知道循环小数长什么样吗?谁能来写1个循环小数?
三位学生分别板书:5.666…,6.272727…,0.314314…
(评析:学生对于循环小数的认识不是一张白纸。教师直接揭题,让学生来写一写,把握真实学情,以学定教。)
二、自学交流,探究新知
(一)自学验证,获取新知
1.自学验证,初步感知。
师:它们是循环小数吗?自学书本第33-34页,找找答案,了解循环小数的相关知识。
(学生自学3分钟)
师:这三个数是循环小数吗?
生:是的。
师:为什么是?
生:因为它们后面有无数个相同的数字。
生:因为后面的数字是重复的。
2.认识循环节,并会简写循环小数。
师:重复的数字,有一个名称叫——
生:循环节。
师:这三个循环小数的循环节分别是——
生:6,27,314。
师:这些循环小数,还可以怎么表示呢?
生:6上面点一个点。
师:5.666…这么多个6,你说的圆点点在哪个6上?
生:点在第一个6上。
师:6.2727…和0.314314…又该怎么表示呢?
生:6.2727…循环点点在第一个2和7的上面,0.314314…循环点点在第一个3和4上面。
师:是的。只要点在第一个循环节的首尾数字上即可。
小结:像这样一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数就叫作循环小数。
(评析:学生通过自学的方式,认识循环小数的循环节和简便写法。教师将教材的编排顺序进行适时调整,将什么是循环小数、循环节和简便写法提前,既顺应学生已有的认知,又为后续探究循环小数之源提供了基本知识。)
(二)三道算式,探循环之源与理
师:通过刚才的自学,你还有什么收获吗?
生:我还知道小数有有限小数和无限小数。
生:我知道循环小数是无限小数。
师:确实,因为循环小数的小数部分有无数个重复的数字,因此它是无限小数,而像1.5这样的小数就是有限小数。你还有其他收获或者疑问吗?
生:我知道两个数相除,有可能得到循环小数。
师:你关注的是循环小数是怎么产生的。这真是一个巨大收获,掌声送给他。他是说循环小数可以由两数相除得到。老师这里有一个算式,会不会产生循环小数呢?(板书:1.3÷3=)
(评析:教师引导学生发现和提出问题:循环小数是怎么产生的?这是本节课的核心问题。学生通过教材例题的自学,不难发现:两数相除可以得到循环小数,这在学习本课前学生是不清楚的。由此激发了学生探究的兴趣,引发对核心问题“循环小数产生之缘由”的深入研究。)
1.计算1.3÷3,理解“相除”可以得到循环小数。
学生在练习纸上独立计算,教师巡视,寻找典型算法(循环节特别长、竖式商带省略号)并板书于黑板上。
师:做好了吗?请看黑板,这是一位同学的计算过程,商是循环小数吗?
生:是循环小数,因为商一直重复出现“3”。
师:为什么商“3”会重复出现呢?请把你的想法与同桌说一说。
(学生思考,同桌交流想法,并汇报)
生:因为竖式中3×4=12,商4,13-12余1,添0,3×3=9,商3,又余1,再添0,3×3=9,商又是3,余数又是1。余数一直是1,添0,商也一直是3,永远写不完。
师:谁听懂他的意思了?
生:他的意思是竖式计算过程中总是“余1”,添0后继续除,商一直是3。
师:你能上来指着板书竖式,说说你的理解吗?
(学生上台指着板书,解释商循环的原因)

师:我们一起来看竖式。三四十二,余1,添0,对应商3,三三得九,余1,添0,对应的商又是3,继续往下算三三得九,余1,添0,对应商还是3。原来是由于余数1的依次不断重复出现(板书:依次不断重复),使得商出现了循环小数。(教师边小结,边完善上图中的板书)
师:在计算中,除法竖式除到哪一位,竖式中的商就写到哪一位。很多同学竖式商写了省略号,这是错误的,此处省略号不用写。(擦掉原先竖式商的省略号)省略号在横式中要表示出来,板书横式中的商:0.4333…,也可以简写成:0.43·。
(评析:教师在本环节想要达成两个目标。目标1:确定两个数相除是可以产生循环小数的,找到循环之源;目标2:理解为什么商“3”重复出现,是由于“余数1”的依次不断重复出现引起的,理解循环之理。)
2.计算86÷11,理解“相同余数第二次出现”可以产生循环小数。
师:原来两个数相除真的可以产生循环小数,我们一起再来试一试。(师板书:86÷11)
学生独立计算,教师寻找竖式“写得很短的”案例,并板书于黑板上。
师:计算好了吗?答案是多少?

师:这里有一位学生是这样做的(如右图)。仔细观察,你看得懂吗?他的计算过程产生循环小数了吗?
生:没有产生,因为商中出现81,你怎么知道接下来一定是81重复呢,可能是812812重复都有可能,我觉得算到这里还不能判断。
生:我也认为是不对的。循环小数要商不断重复出现,现在还没有重复出现。
生:我有不同意见。我觉得可以判断商一定是循环小数了,因为你看现在余数是9,那么添0,往下算的话,商就是8,再算商就是1,它就是81循环。
……
(学生争论不清)
师:那想象一下,如果继续往下算,会怎么样呢?
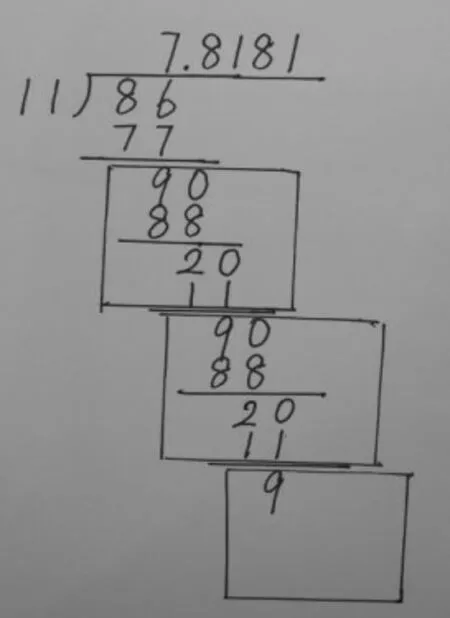
学生说计算过程,教师板书竖式。(形成右图竖式,注:此时还未有线框)
师:现在你们有什么发现?
生:下面算的过程和之前的是一样的,不断重复了。师:什么地方是一样的,上来指一指。(学生上台指相同过程)
师:他的意思是第二步过程和原有的第一步是一样的,这一步对应的商是81。那没有算完的这一步(最后的余数9),对应的商是81。
小结:这位同学只算到余数9第二次重复出现,就判断循环节是81是可行的。因为,余数相同,计算下一步就会重复上一步过程,也就产生了循环。
(评析:为什么余数第二次重复出现,就能判断商是循环小数呢?这是一个有挑战性的问题。教师在展示“短”作品后,充分让学生思辨,有学生赞同,有学生不赞同。交流过程充分展现学生质疑探究的能力。)
3.计算41÷37,谁能最快找到循环节。
师:下面我们进行比赛,看谁能最快找到41÷37商的循环节。
(学生独立计算,教师巡视,寻找较快完成的同学)
师:找到循环节了吗?是多少?
生:找到了,循环节是108。
师:(投影学生作品:短的)这是很快找到循环节的同学,仔细观察,和他过程一样的举手。
师:顺便检查一下,108循环,你的循环点点对了吗?
(学生互相检查有没有正确表示)
师:通过刚才的3次计算,你对循环小数有了什么更深的认识?
生:我知道循环小数是两个数除出来的。
生:我知道如果余数依次不断重复出现相同的数字,商也不断重复。
生:我还理解了余数只要第二次重复出现,就可以判断是循环小数了,不用计算很多位。
(评析:采用比谁最快找到循环节的教学方式,使得在一堂课的后半段,学生的学习兴趣被再次激发,既巩固了教学成果,又使学生对于循环小数的产生有了更深刻的认识和理解。)
三、巩固练习,拓展提升
(一)比大小
(二)确定循环节
师:昨天老师计算了1.5÷7,计算过程课件会慢慢呈现,当你确定商的循环节了,就站起来示意。
课件一步步呈现竖式过程,到右图所示结果时,有很多学生站起来了。
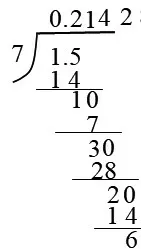
师:为什么计算到这里,你们就确定了循环节呢?
生:因为商重复出现2了。
师:是这样的吗?你为什么没有站起来?
生:我觉得到这里还无法判断,因为再算下去,6添0,商是8了,不是1,还没有出现重复。
生:我们判断循环小数不是看商的数字有没有重复,而是看竖式中余数有没有重复,而这里余6,上面没有6,所以还不能判断。
师:解释得真好,判断商是不是循环小数,关键看:余数有无重复出现(指板书:重复出现)。
课件继续呈现计算过程,到如上右图所示,学生认同可以判断循环节是:142857。

(评析:课堂很活跃,学生能判断了就站起来。很多学生看到商重复出现2时就站起来了,这时教师没有急着算下去,而是组织生生交流,让站起来的学生自然意识到应该关注的是竖式中的余数有无重复出现,再次经历了难点的理解巩固。)
(三)你知道吗
师:现在我们通过课件观看一些循环小数。

(评析:这一环节拓展了学生对循环小数的认识,激发了学生学数学的兴趣,例如学生观察发现:循环节的位数最大是比除数小1,思考为什么小1,培养学生发现问题和提出问题的能力。)
四、全课总结,交流感受
师:今天这节课学习了循环小数,你对循环小数有什么新的问题要提?
生:学习循环小数,有什么用?
生:两数相除商有可能是无限但不循环的小数吗?
生:为什么刚才“你知道吗”这几个例子,循环节的位数比除数小1?
……
师:同学们提出的问题都很有探究价值,这些问题的答案有兴趣的同学可以课余去探究,通过查资料了解。
(评析:总结交流环节,教师又组织了一次发现和提出问题,引发学生进一步思考循环小数还有哪些知识可以去探究,这也是学习数学的乐趣。)
【总评】
这是一堂层次分明的数学课,教师在教学中充分体现了以学生为主体的理念,主要表现在以下三点。
一、把握学情,以学定教
学生对循环小数的认知不是零起点,教师把握了学情。课始让学生写循环小数,通过自学的方式加以验证,同时把循环节及简便表示很有效率地教学完。这样的处理方式,优点在于:(1)尊重学情,学生已经知道的、自学能会的知识,就应该放手让学生展示,在自学和交流中不断完善认知;(2)留足空间,探究循环小数产生的原因是本课的重点难点。
二、突出重点,深度学习
本课知识点较多,包含了循环小数的定义、产生过程、读写方法、认识循环节、商的分类、无限小数和有限小数的定义等。于老师把理解循环小数产生的原因,作为本课的重点难点,着重探究为什么,而不是是什么。于老师设计了3道不同形式、不同层次的计算题,让学生充分经历了循环小数产生的过程,知道商循环的原因是由于余数重复出现引起的。学生掌握了只要余数第二次重复出现,就不必再除,可以确定商的循环节。
三、发现问题,提出问题
培养学生发现问题和提出问题是数学教学的重要目标。于老师在课中很好地搭建了发现和提出问题的平台,引导学生进行质疑和交流,帮助学生理解循环小数。如在自学后的交流环节,于老师问:自学后你有哪些收获或者疑问?意在让学生关注循环小数的产生。又如在课尾问:你对循环小数有什么新的问题要提?意在引发学生的深入思考,激发探究欲望,这是比获得知识更重要的环节。

