例谈解三角形试题中的考虑不周

余铁青

(广东省中山市桂山中学 528463)

解三角形试题在三角函数板块内容里面综合性相对较强，而这类试题多半考查的都是学生的推理与运算能力.作为初学此部分内容的学生，在做题考试过程中经常会忽略隐藏在题目中的客观存在的条件.由于这样的考虑不周产生了很多错误.下面我们将从以下实例分析试题中的一些陷阱，以期引发大家去发现思考.

一、忽略三角形内角和致错

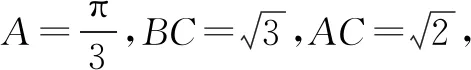
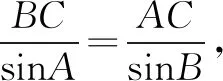
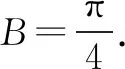
二、忽略三角形边长关系致错

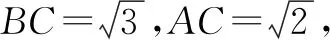
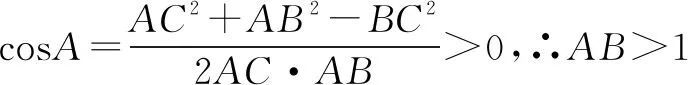
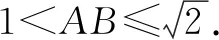
三、忽略函数定义域致错

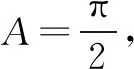
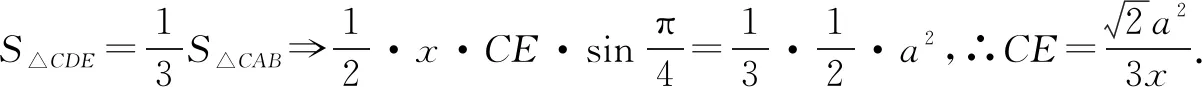
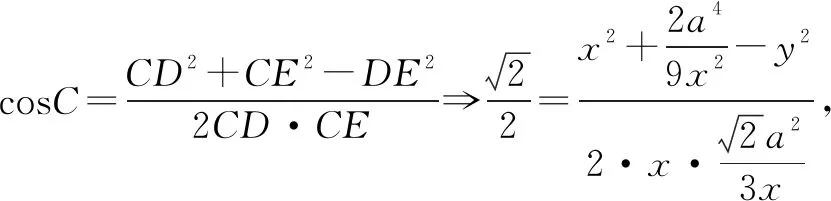
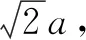
四、忽略三角函数的有界性致错

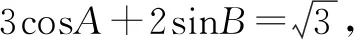
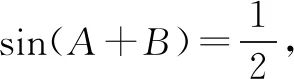
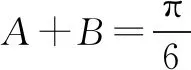
五、忽略角所在象限致错

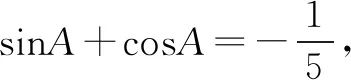
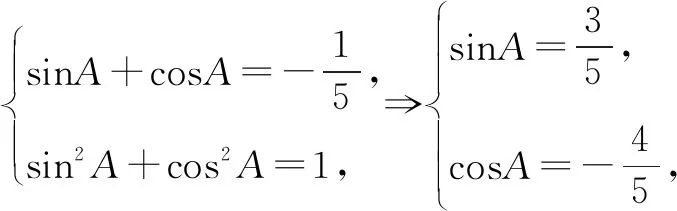
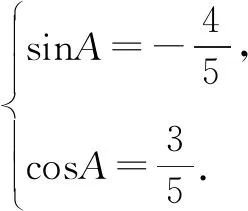
六、忽略相互函数关系致错

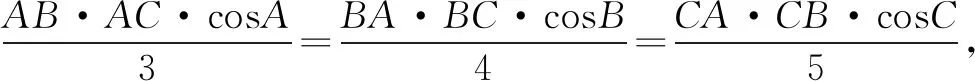
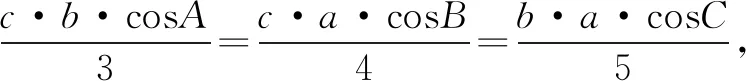
于是进一步化简得到：

3tanA=4tanB，3tanA=5tanC,

所以tanA∶tanB∶tanC=20∶15∶12.

下面假设

tanA=20，tanB=15，tanC=12，

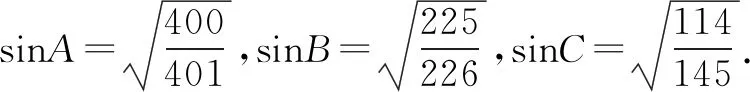
再次结合正弦定理知：

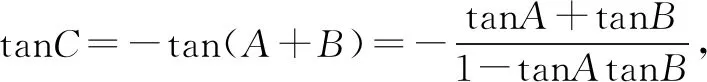
处理解三角形问题主要是能够准确选用正弦定理，余弦定理，面积公式以及相应得一些变形推广结论，在此之中还要时刻注意是否会出现不合题意的结果，其中就有上面的这六类情况，值得注意的是题型千变万化，但究其本质仍然是在考查学生的计算能力，以及考虑的周全性与完整性，那么学生的做题意识就要强烈一点，时刻提醒自己做题既不能画蛇添足更不能考虑不周.