例析零点虚设在解导数解答题中的应用

李 宁 贺航飞

(海南省海南中学 571158)

导数是研究函数性质的重要工具. 导函数的零点在研究函数单调性和极值时起着关键作用. 有时候导函数的零点存在但是不可求，这时就可以虚设零点参与接下来的解题. 下面从不同题型归类剖析虚设导函数零点的应用.

一、在证明不等式中的应用

例1已知函数f(x)=ex-alnx(a∈R,a>0)，证明：f(x)≥a(2-lna).

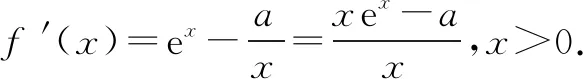
又g(0)=-a<0，g(a)=a(ea-1)>0，从而存在x0∈(0,a)使得g(x0)=0，且当x∈(0,x0)时f′(x)<0，f(x)单调递减；当x∈(x0,+∞)时f′(x)>0，f(x)单调递增. 从而f(x)≥f(x0)= ex0-alnx0.

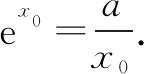
评注本题f(x)的极小值刚好是最小值，而f′(x)的零点x0存在但不可求. 关于x0的信息集中在方程g(x0)=0中，借助此方程灵活变形，化简f(x0)的解析式(设法将其中的指数结构、对数结构等复杂表达式换为较为简单结构).

例2已知函数f(x)=ex-x2，设x≥0，求证：f(x)>x2+4x-14.

证明设g(x)=f(x)-(x2+4x-14)=ex-2x2-4x+14(x≥0).则g′(x)=ex-4x-4，g″(x)=ex-4. 当x∈(0,ln4)时，g″(x)<0，g′(x)单调递减；当x∈(ln4,+∞)时，g″(x)>0，g′(x)单调递增. 又g′(0)=-3<0，g′(2)=e2-12<0，g′(3)=e3-16>0，于是存在x0∈(2,3)使得g′(x0)=0，此时ex0=4x0+4，且当x∈(0,x0)时g′(x)<0，g(x)单调递减；当x∈(x0,+∞)时g′(x)>0，g(x)单调递增.

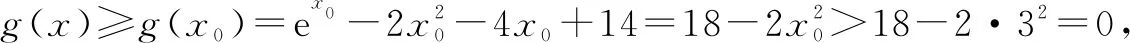
评注对于取不到等号的函数不等式的证明，在作差求导时往往会遇到导函数零点不可求的情形. 在用零点存在性定理确定零点所在区间时，应尽可能让这个区间长度变小. 在解析分析的过程中，可以先取一个大致区间，后期如果这个区间不能满足需求，再回过头调整这个区间.

二、在恒成立求参数范围题型中的应用

例3 已知函数f(x)=xlnx，g(x)=(k-3)x-k+2(k∈Z). 当x>1时，不等式f(x)>g(x)恒成立，求k的最大值.

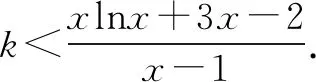
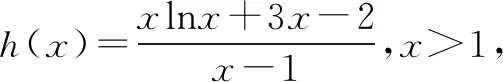
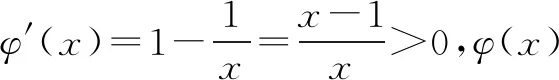
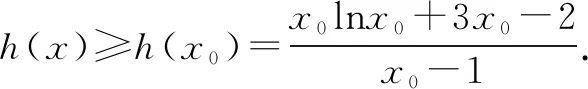
评注分离参数后，问题转化为求函数h(x)的最小值. 在审题时，题目求整数k的最大值，而不是求实数k的最大值，很有可能是k的最大值存在但不可求，只能估算. 本题也可以不分离参数，采用先取特殊值必要性探路再证充分性的方法解决，即：由f(2)>g(2)得k<4+2ln2，由于k∈Z，从而k≤5. 容易证明当k=5时f(x)-g(x)>0恒成立，故整数k的最大值为5.

三、在零点问题中的应用

例4 已知函数f(x)=ax2-x-lnx,a∈R. 若函数f(x)有两个零点，求实数a的取值范围.

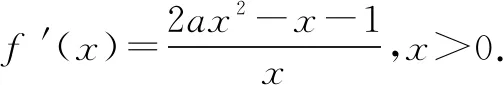
(1)当a≤0时，f′(x)<0，f(x)在(0,+∞)上单调递减，不可能有两个零点.

(2)当a>0时，设g(x)=2ax2-x-1，则二次函数g(x)开口向上且g(0)=-1<0，从而存在x0>0使得g(x0)=0，且当x∈(0,x0)时g(x)<0，f(x)单调递减；当x∈(x0,+∞)时g(x)>0，f(x)单调递增.

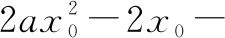
综上所述，实数a的取值范围为(0,1).

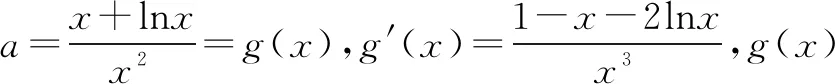
四、在极值问题中的应用

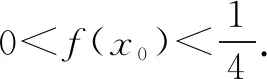
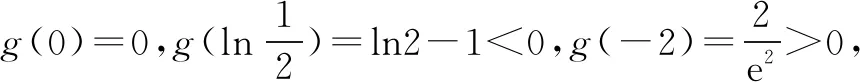
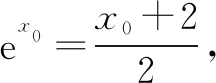
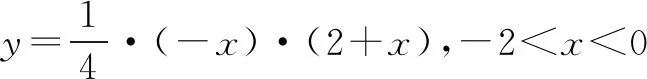
相关练习：

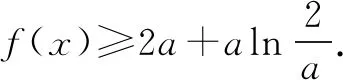
2.已知函数f(x)=x2-x-xlnx，证明：f(x)存在唯一极大值点x0，且e-2

3.若k∈Z，当x>1时，不等式xlnx+x>k(x-1)恒成立，求k的最大值.

4.已知函数f(x)=ln(x+1)+ax2(a>0)，若函数f(x)在区间(-1,0)有唯一零点x0，证明：e-2