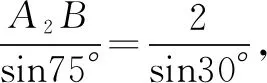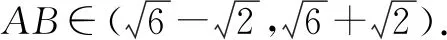强化思想意识 指引解题方向——例谈解三角形中的取值范围与最值问题的求解

吴利华 朱贤良

(安徽省枞阳县宏实中学 246700)

解三角形问题一直是高考数学的必考点，在解三角形的背景下，设置与边长、角度、周长、面积等相关的取值范围与最值问题，成为十分常见的命题角度，受到命题者的青睐.这类问题注重与函数、不等式和几何等知识的交汇融合，涉及的知识面广，灵活性大，综合性强，求解时需要充分利用正余弦定理、面积公式、三角形的内角和定理，并结合平面几何、基本不等式以及函数值域与最值等知识来实现破解.本文结合典型例题，对解三角形中的取值范围与最值问题的求解思路做一梳理与归纳，供读者朋友研读与参考.

一、函数思想

函数描述了自然界中数量之间的关系，函数思想强调通过提出问题的数学特征，建立函数关系型的数学模型，是一种用函数的概念和性质去分析问题、转化问题和解决问题的思维策略，它体现了“联系和变化”的辩证唯物主义观点.函数思想堪称是破解取值范围与最值问题的神兵利器，最具普适性与有效性.

点评运用函数思想解决此类问题有两个关键步骤：一是合理选择自变量以建立函数关系，二是准确求解函数值域或最值.

(1)求B；

(2)若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围.

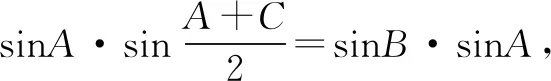
(2)根据三角形面积公式，可得

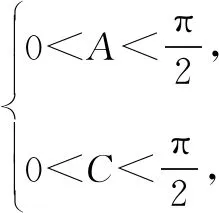
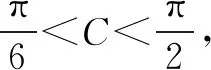
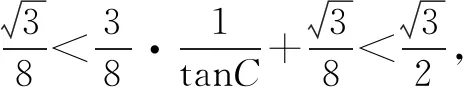
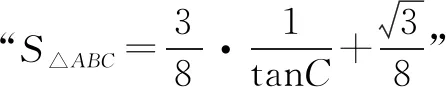
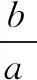
解析因为函数f(x)=x2+c2-a2-ab有唯一零点，则c2-a2-ab=0，结合余弦定理整理得a=b-2acosC，再结合正弦定理变形得sinA=sinB-2sinAcosC，即sinA=sin(A+C)-2sinAcosC，即sinA=sin(C-A)，故A=C-A，即C=2A.

由正弦定理，有

注意到△ABC为锐角三角形，则

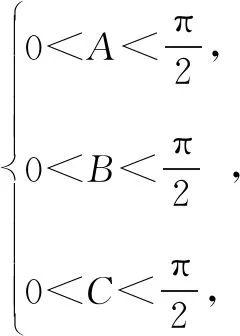
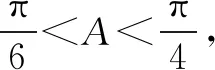
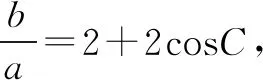
二、基本不等式

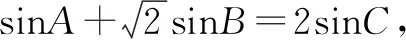
点评先根据正弦定理化角为边，再利用余弦定理和均值不等式，求得cosC的最小值，体现了转化与化归的数学思想.

例5 (2014年高考全国Ⅰ卷·理16)已知a,b,c分别为△ABC三个内角A,B,C的对边，a=2，且(2+b)(sinA-sinB)=(c-b)sinC，则△ABC面积的最大值为____.

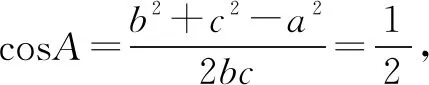
再由基本不等式，bc=b2+c2-a2≥2bc-4，故bc≤4.

点评本题的实质是将“由bc=b2+c2-4求取bc的最大值”这一基本不等式问题完美镶嵌入解三角形问题之中，体现了在知识交汇处命题的原则.

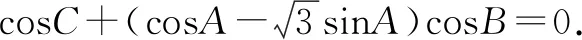
(1)求角B的大小；

(2)若a+c=1，求b的取值范围.

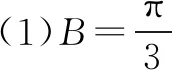
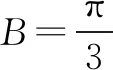
点评第(2)问也可以利用正弦定理与三角形内角和定理将b转化为角A或C的三角函数求得取值范围，还可以借助a+c=1将b2=1-3ac转化为关于边a或c的函数表达式求得值域.

三、解不等式(组)

在求解某些解三角形中的取值范围问题时，可以先考虑根据题设中的限制条件，等价地列出边与角等变量所满足的不等式(组)，再解之即得对应变量的取值范围.需要注意的是，在罗列不等式或不等式组时，应该使之与题设互为充要条件，否则会误将取值范围放大或是缩小.

例7 已知1,3,a为钝角三角形的三边之长，则a的取值范围是____.

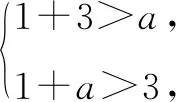
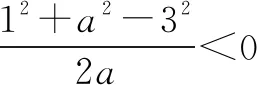
点评列不等式组时，要充分考虑1,3,a围成三角形(任意两边之和大于第三边)，且是钝角三角形(最大角为钝角).

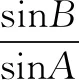
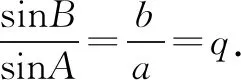
点评借助三角形两边之和大于第三边，进而列出关于q的不等式组是解题的重要一步.

四、轨迹思想

正是由于动点的存在，让三角形中的边长、角度具有不确定性.如果能够弄清楚动点的运动规律，厘清变量与动点之间的联动规则，则能为问题的解决提供新的思路.换而言之，在某些解三角形问题中，抓住动点轨迹，从轨迹的角度着手，可以实现巧妙求解.

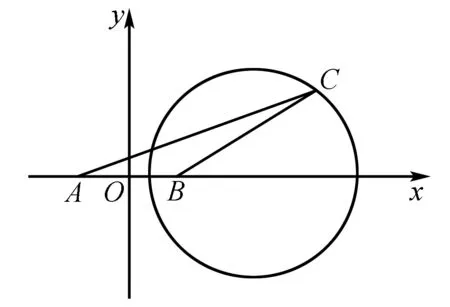
图3

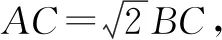
点评本题看似与解析法无关，实则暗藏了动点的轨迹问题，从而实现乾坤挪移、移花接木.运用解析法来求解这类问题，可以避免繁琐的三角计算，简洁明了地获得问题的答案.

例10(2015年高考新课标全国Ⅰ卷·理16)在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是____.

分析作为一道解三角形问题，首要的问题是弄清“三角形”在哪里，即解哪一个三角形，故考虑连接四边形的任一对角线.如图4，在△ABC中，BC=2，∠B=75°，利用解三角形知识与函数思想可求AB的取值范围.

换个角度，我们也可以尝试从画图的角度来确定AB的变化规律.如图5，先画定线段BC=2，继而以BC为公共边作∠B=∠C=75°，再在∠B的另一边上选一点A，作∠BAD=75°交∠C另一边于点D，即得与题意相符的四边形ABCD.显然点A在线段A1A2上运动(不含两端点).

解法一如图4，连接AC，设∠BAC=θ，则∠ACB=105°-θ.

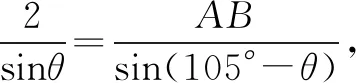
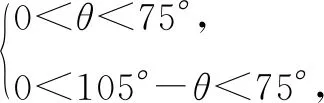
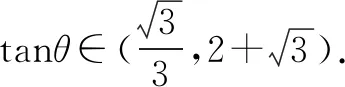
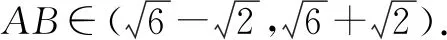
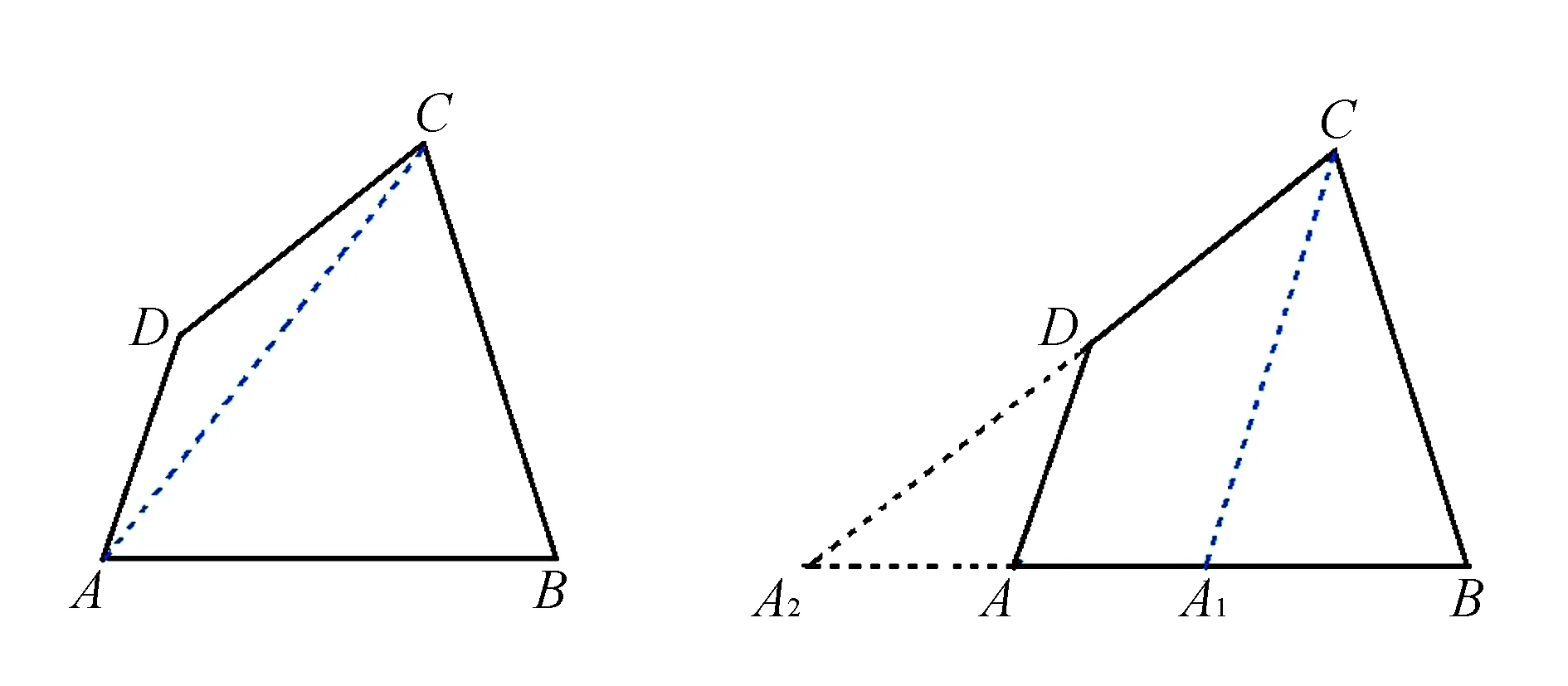
图4 图5

解法二如图5，作CA1∥DA交AB于点A1，延长BA、CD相交于点A2，则点A在线段A1A2上运动(不含A1,A2)，即A1B

点评取值范围与最值问题最普遍的求解方法是利用函数思想，如解法一，关键在于合理选择自变量，进而构建函数关系式，解法厚重而大气.解法二从运动的角度入手，着重理清点A的运动轨迹，直观而轻盈.