2018年广州一模理科12题的求解探讨

王晓川

(广东省汕头经济特区林百欣中学 515000)

题目(2018·广州一模理·12)设函数f(x)在R上存在导函数f′(x)，对于任意的实数x，都有f(x)+f(-x)=2x2，当x<0时，f′(x)+1<2x，若f(a+1)≤f(-a)+2a+1，则实数a的最小值为( )

本道试题是以抽象函数为载体，以导数为工具，以解不等式为落脚点.该题涉及抽象函数的性质，用导数工具研究函数单调性，解不等式等内容.抽象函数由于没有具体的解析式，因此它就像“神”一般的存在，具有很高的隐蔽性和抽象性，问题较为复杂，问题研究难度较高.该类问题的求解对数学综合能力的要求较高，因此该类问题常以压轴题的形式在试题中呈现.本题是2018年广州市高考第一次模拟考试理科数学选择题的压轴题，从测试结果来看真正达到了压轴的目的，得分率很低.

思路一：构造特殊函数

解法1要构造同时满足对于任意的实数x，都有f(x)+f(-x)=2x2和当x<0时，f′(x)+1<2x的特殊函数.

首先观察等式f(x)+f(-x)=2x2的右边是2x2，因此可以确定函数f(x)的解析式里一定含有x2.同时还要考虑当x<0时f′(x)+1<2x，因此可以确定函数f(x)的解析式里还有含有kx，且k+1<0即k<-1.

此时可以令f(x)=x2+kx(k<-1)，不妨令k=-2，得f(x)=x2-2x.

所以f(x)+f(-x)=x2-2x+(-x)2-2(-x)=2x2，f′(x)=2x-2，

所以f′(x)+1=2x-2+1=2x-1<2x满足题意.

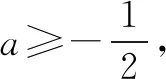
评注构造特殊函数将抽象函数的“隐蔽性”“显性化”对问题的解决大有帮助.我们可由f(x)+f(-x)=2x2得知函数f(x)的解析式里一定含有x2这一项，这一点不难理解，但若f(x)=x2，则f′(x)=2x显然不满足f′(x)+1<2x.考虑到等式f(x)+f(-x)=2x2的左边f(x)和f(-x)，x与-x互为相反数，而等式f(x)+f(-x)=2x2的右边只有2x2，因此可以确定函数f(x)的解析式里还含有kx这一项，同时还要考虑到当x<0时f′(x)+1<2x，所以k+1<0即k<-1.此时就可以构造特殊函数f(x)=x2+kx(k<-1)，为解决问题更加方便，k可以取满足k<-1的具体整数，后面问题的解决就比较容易了.因此说，构造特殊函数解决有关抽象函数导数不等式问题，尤其是客观题是一种很不错的选择，效率更高，达到小题巧做得目的.

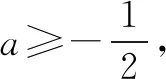
评注解法2与解法1思路差不多，主要是如何想到构造特殊函数，解法2与解法1的思路切入点有所差异.

思路二：构造一般函数

解法3 对于任意的实数x都有f(x)+f(-x)=2x2联想到函数的奇偶性，故设f(x)=x2+g(x)，所以函数g(x)=f(x)-x2为奇函数.

又由当x<0时f′(x)+1<2x，即f′(x)-2x<-1，所以g′(x)=f′(x)-2x<-1，所以函数g(x)在(-∞,0)上单调递减，又g(x)为奇函数，g(x)在R上单调递减.

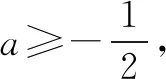
评注该解法是该类问题的一般解法，但算理不好理解，众多考生很难想到这样解.如：“对于任意的实数x都有f(x)+f(-x)=2x2”如何联想到函数的奇偶性？退一步说，就算能联想到函数的奇偶性，那又怎样想到要构造f(x)=x2+g(x)？又怎样想到g(x)为奇函数？能想到这些的学生很不一般，肯定少之又少，对于很多考生来说想到这些就不是那么自然！这些恰恰是他们解该类问题的“思维痛点”.由于解题“思维不通”，于是“痛不欲生”，正所谓“痛则不通，通则不痛”.相比之下解法1就显得亲切很多，更容易让人理解，更容易让人接受.但要想根据题意快速想出特殊函数并不容易，需要日积月累，勤于思考，勤于实践，方可具备敏锐的洞察力和快速解答问题的能力.