“深”一题 “度”一类——一道简单数列不等式试题的深度探究

沈海全 田晓敏

(1.浙江省绍兴市越州中学 312000;2.浙江省丽水市缙云县工艺美术学校 321400)

原本祥和、安宁的春节被一场突如其来的疫情打乱. “抗疫”成了2020年新春的主题词.在这场紧张的战“疫”斗争中，老师们积极响应号召，在全民抗击疫情的斗争中贡献力量. 笔者也积极投入到“停课不停教，停课不停学”的工作中. 一次在对一道简单数列不等式试题的网课教学中和学生无意间擦出了思维的火花，觉得有必要写出来，意在抛砖引玉.

一、一题“二引申”

引例已知数列{an}和{bn}满足b1=2，b2=4，2an+1=an+an+2，且数列{anbn}的前n和为(n-1)·2n+1+2,n∈N*.

(1)求数列{an},{bn}的通项公式；

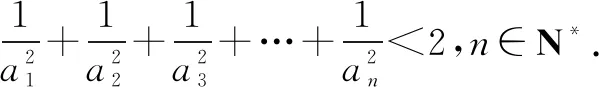
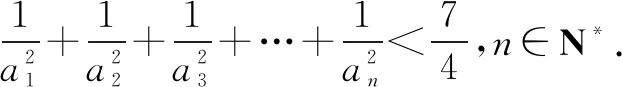
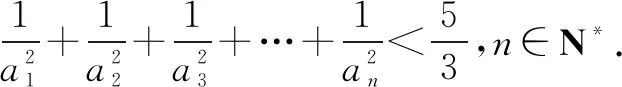
解(1)因为数列{anbn}的前n和为(n-1)·2n+1+2，所以当n=1时，a1b1=2；

当n≥2时，anbn=((n-1)·2n+1+2)-((n-2)·2n+2)=n·2n，由b1=2，b2=4，可解得a1=1，a2=2，又因为2an+1=an+an+2，所以数列{an}为等差数列.由等差数列通项公式可得an=n，从而bn=2n.

(2)因为当n=1时，不等式显然成立.

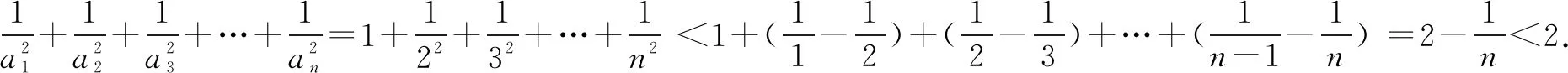
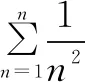
引申1解法一当n=1,2时，不等式显然成立.当n≥3时，

引申1解法二当n=1时，显然成立.

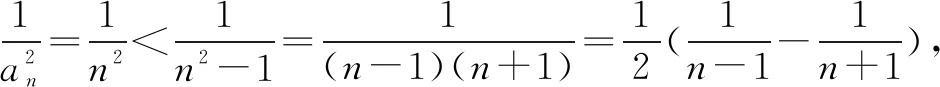
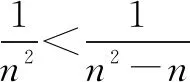
引申2解法一易知n≤5时不等式成立，当n≥6时，

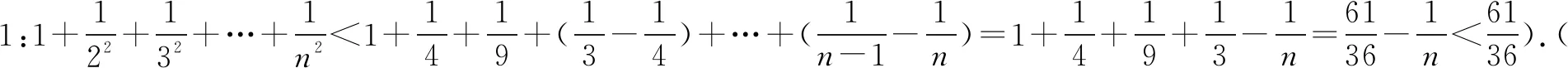
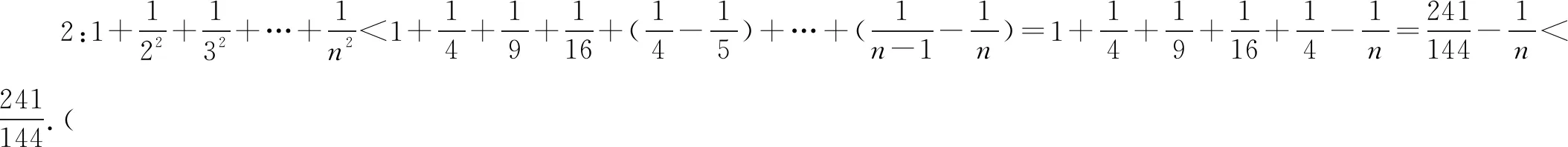
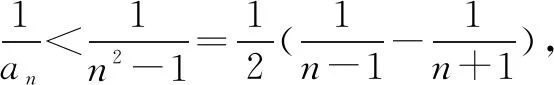
引申2解法三

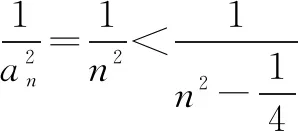
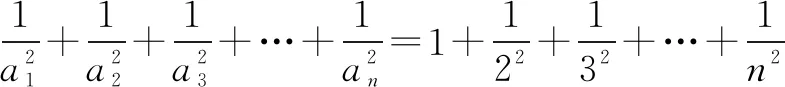
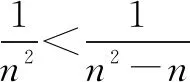
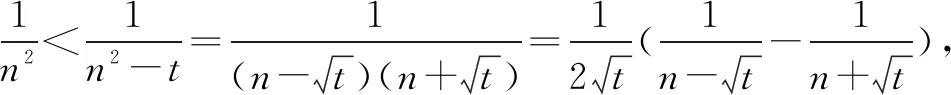
二、一题“七变式”

我们发现引例第一问解得的结果为我们最熟悉的等差、等比数列，由等差an构造了第二问，那么能否由an，bn再发散一些新的问题呢？下面请看

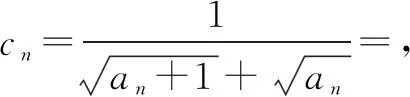
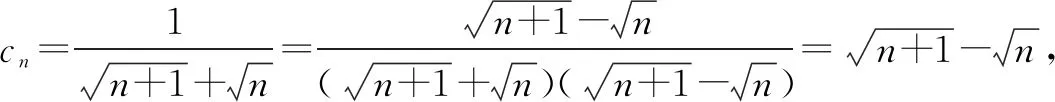
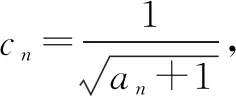
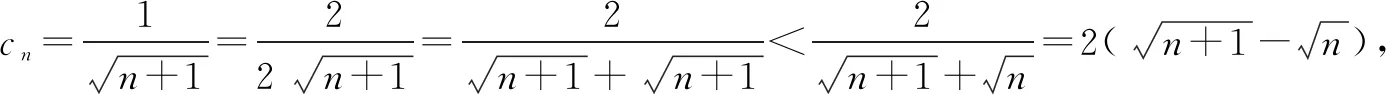
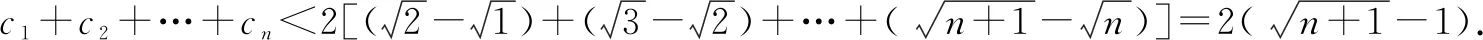
评注变式1由an构造了带根式的通项，熟悉的类型直接可以叠加相消求和后证明. 变式2是在变式1的基础上进行拓展，发现可以放缩为变式1，从而证得结果.

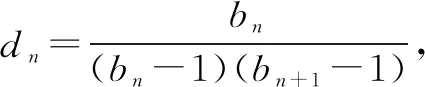
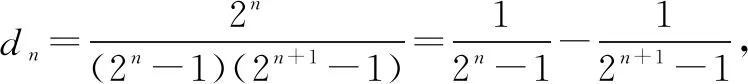
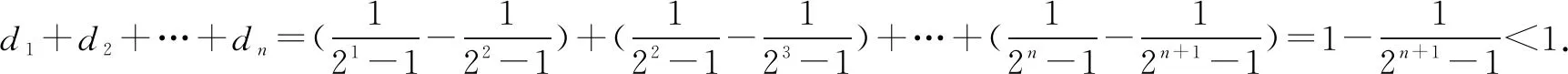
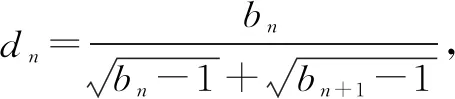
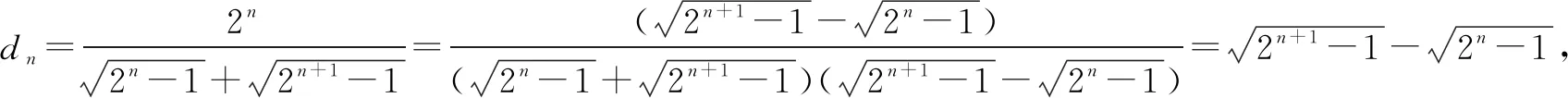
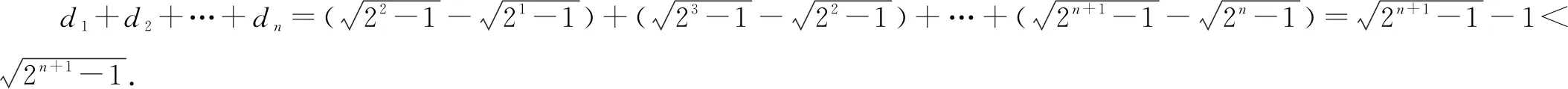
评注变式3是由bn构造成了指数型可裂项相消求和的通项，变式4是在变式3的基础上，拓展为带根式的指数型叠加相消问题. 但变式3、4都能直接求和.

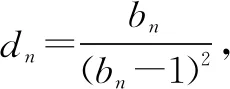
解当n=1时，显然成立；当n≥2时，

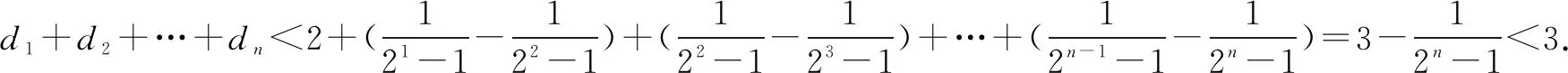
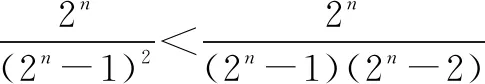
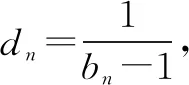
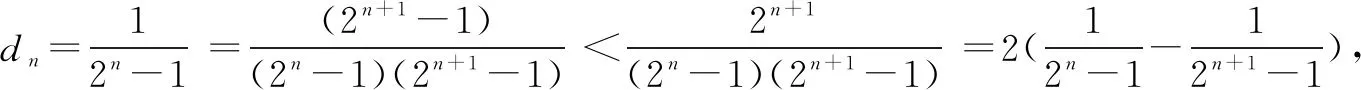
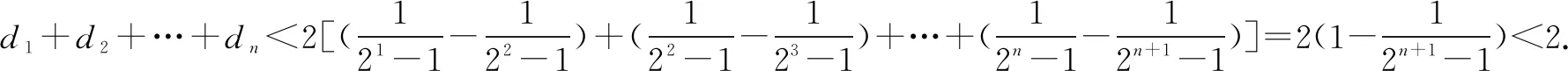
解法二当n=1时，显然成立；当n≥2时，

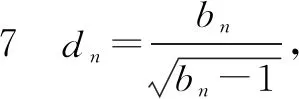
证明因为

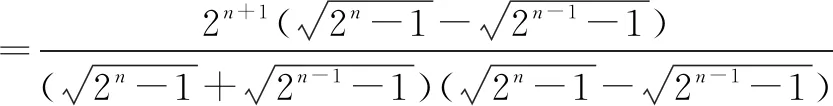
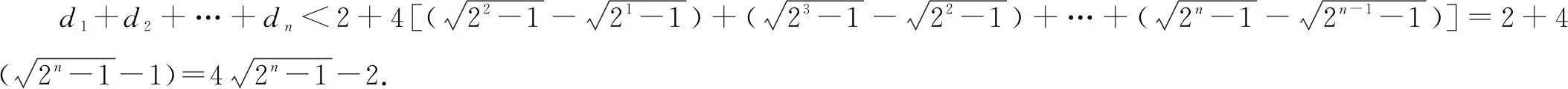
评注变式5到变式6是模仿了变式1到变式2的过程，解法一放大为指数型裂项相消，解法二放大为“等比型”求和. 变式7在变式6的基础上加进根式型.

一题“二引申”、“七变式”促成“深”一题，“度”一类. 若我们数学教师在解题教学中能够引导学生阶梯式的、促进式的“深度”学习，我们的数学课堂会更高效、更有思维深度，学生的知识体系、思想方法体系会更系统，从而幸福的数学课堂不再是梦想.