基于蚁群算法的基因位点组合与眼压数据的相关性分析
曹一鸣 胡 曼 徐永利*
(1.北京化工大学 数理学院, 北京 100029; 2.北京儿童医院 眼科, 北京 100045)
引 言
基因的多位点组合与表型的关联分析是生物信息学的研究热点,近年来的研究表明,在对复杂性遗传疾病的分析上,相比于单基因位点,多基因的多位点组合与表型的关联更为显著。然而,现有的方法仅适用于分析多位点组合与离散型表型的关联,不能分析其与连续型表型的关联。
原发性青光眼属于复杂遗传病[1],是全球第二位的不可逆性致盲眼病[2-3],在我国,原发性青光眼(不包括先天性青光眼)的致盲率约为10%[4]。原发性开角型青光眼(primary open-angle glaucoma,POAG)的单眼致盲率在北京市农村和市区分别为15.4%和10.90%[5]。在我国,患青光眼的人群中原发性以及先天性青光眼患者的比例占80%以上[6]。针对青光眼进行基因层面的进一步研究有助于对该疾病的早期诊断。病理性眼压升高是大部分青光眼患者都会出现的临床症状,在一项大型多队列研究中,发现眼压(intraocular pressure, IOP)与原发性开角型青光眼之间存在着强烈的关联[7]。因此研究与眼压相关的变异有助于发现更多影响青光眼发病的基因。
测序技术的进步使研究人员可对大规模样本数据进行测序,同时可纵向比较一大批样本的基因组。全基因组关联分析(genome-wide association study,GWAS)是一种在全基因组层面上的无假设分析(即关于特定基因或基因座位无现有的假设,但也不存在这些基因之间关联的零假设),其对跨基因组和疾病的标记(单核苷酸多态性,即SNP)之间的关联进行测试,通常涉及300 000个或更多合理多态且在基因组中平均分布的标记[8]。近年来,GWAS试图进一步研究多个SNP对个体表型差异的综合作用,从而衡量它们对疾病发病的影响大小。
传统GWAS一般通过对Case-Control数据的分析来筛选出能够影响复杂遗传病的SNP位点。2012年,一项基于单位点对青光眼作用的GWAS研究[9]给出了结果,即经过T检验后具有较高显著性的两个单位点:位于17号染色体基因GAS7上的rs11656696和位于1号染色体基因TMCO1上的rs7555523。然而对于复杂遗传病,它在基因层面的致病机理不能仅通过几个SNP位点单独的作用得到解释,考虑多个位点的共同作用和上位性相互作用等一系列基因间的相互作用关系非常必要[10]。
近年来,一些学者通过对Case-Control数据的分析,在多个SNP位点组合与疾病关联性的研究方面已经取得了一些成果。Sapin等[10]利用蚁群算法对Ⅰ、Ⅱ型糖尿病,肠炎和类风湿性关节炎4种疾病进行了研究,在4个数据集上均发现了对疾病影响统计显著性较高的双SNP位点组合。Liu等[11]利用Hi- seeker模型在对乳腺癌和小肠吸收不良症的Case-Control数据研究中,发现了对疾病影响统计显著性较高的三SNP位点组合。以上两种方法都是针对Case-Control数据(每个病例的状态是患病或健康)的分析,而与POAG之间存在强烈关联的眼压数据是连续变化型数据,每个病例的眼压值可以是确定范围内的任意实数,而不是有限的几个状态。据我们所知,针对连续型数据和SNP位点的关联性分析目前还没有相关研究。
本文设计了一种蚁群算法,用来从数以亿计(约1.767×1011对)的双位点组合里筛选与眼压最为相关的组合。利用本文设计的蚁群算法,对欧洲生物信息学研究所(European Bioinformatics Institute,EBI)所辖数据库中一项记录了样本人群眼压和基因的原发性青光眼数据进行分析,并从中发现了一些具有较高统计显著性的双位点组合;特别是在2号染色体上发现了多个SNP位点与同一个基因具有较高的显著性关联,这意味着在此数据集上可能存在一些特定位点,通过上位性相互作用影响其他基因的表达量。
1 算法部分
1.1 蚁群算法
蚁群算法是一种启发式算法,能够在节省计算资源的前提下从大量数据中发掘出有效信息。相比于遍历方法的计算复杂度O(n2) (n为总位点数),蚁群算法的计算复杂度为O(m) ,其中
m=genmax×n_ant
(1)
式中,genmax表示最大迭代次数,n_ant表示蚂蚁个数。相比于遍历计算平方阶的时间复杂度O(n2),蚁群算法的计算复杂度为线性阶O(m)。
本文借鉴了Sapin等[10]用来分析Case-Control数据的算法,设计出一种通过研究连续型变量和双SNP位点组合之间的关联,来寻找可能具有致病性双位点组合的蚁群算法。通常的蚁群算法是一种探索优化路径的概率型算法,蚂蚁个数表示每一次算法迭代中可行解个数的参数。蚂蚁从随机起点开始,移动到与当前节点有连接的下一个节点上。在选择下个节点的过程中,蚂蚁会根据满足条件的节点上信息素值的大小,对较大信息素值有偏向性地随机决定下一步,某节点信息素值越高则蚂蚁选择该节点的概率越高。节点被选择后,蚂蚁在选择的节点上按一定规则留下一定量的信息素。在本文设计的算法中,信息素用来刻画每个SNP位点对于预测眼压的重要程度。
提前为算法设置初始信息素值、蚂蚁个数、竞赛规模、禁忌频率这4个参数。另外,由于没有明确终止条件,需要设定最大迭代次数genmax。设置参数后进入算法的循环部分。在算法的每一次循环中,首先采用竞赛选择为每一只蚂蚁找到一个初始的双位点组合,即让每只蚂蚁随机且具有偏向性地从数据集子集中选择SNP组合;然后评估每只蚂蚁携带的双位点组合对受测试者眼压的划分情况,并计算适应度函数;循环的最后,对本次循环最优的双位点组合进行信息素更新,相应信息素值P(SNP1)+P(SNP2)叠加在双位点组合的每个SNP上;最后,在所有SNP位点上乘一个小于1的常数r_loss作为信息素值的损失率,以此来蒸发一定量的信息素值,本文中使用了0.99这个乘数值。
又考虑到某些位点的信息素值可能过高,从而频繁出现在迭代中,因此本文算法结合了禁忌表每隔一定的子循环数(1 000次)禁忌信息素最高的一个位点。从生物学意义上来说,由于基因间相互作用的影响,两个单体作用都不大的SNP位点也可能组成对青光眼发病影响很大的位点组合,这样的组合较难被发掘,未被解释的青光眼遗传机制极有可能在这些位点组合中。结合禁忌表可以找到更多诸如此类对青光眼发病综合作用大、而组合中单个位点影响都很小的双位点组合。
传统的蚁群算法使用轮盘赌法进行路径选择,轮盘赌法又称为比例选择法,其基本思想是各位点被选中的概率与其信息素大小成正比。该方法能选择既随机又偏向于具有最大信息素的路径。由于本文基因数据包含数量巨大的SNP(单位点个数接近600 000个),当变量数很高时,直接使用轮盘赌法对计算量消耗会成倍增长。因此,本文在轮盘赌法之前加上竞赛选择步骤。竞赛选择即先随机选择一个指定大小的位点子集,再在这个子集上用轮盘赌法选择2个SNP。
1.2 算法流程
基于1.1节分析设计的算法,设计伪代码如下。
1)初始化参数(蚂蚁个数n_ant和最大迭代次数genmax),将每个SNP位点上的信息素初始化为0;
2)repeat以下步骤:
3)for 所有蚂蚁 do:
4)通过竞赛选择为每一只蚂蚁找到两个SNP位点的双位点组合;
5)计算每一只蚂蚁的双位点组合的适合度函数值;
6)end for;
7)更新具有最高适应度函数值的两个SNP位点的信息素;
8)for 所有SNP位点 do:
9)乘以损失率r_loss来蒸发一定量的信息素;
10)end for;
11)每隔一定迭代次数禁忌信息素最高的一个位点;
12)until最大迭代次数后终止循环。
上面描述的算法伪代码中,主要包括3个步骤:
步骤1初始化参数(设置蚂蚁个数,最大迭代次数,竞赛规模和禁忌频率),将每个SNP上的信息素初始化为0,然后对步骤2迭代genmax次;
步骤2通过竞赛选择为每一只蚂蚁找到包含两个SNP位点的组合,计算每一只蚂蚁位点组合的适合度函数,更新具有最高适应度函数值的两个SNP的信息素,最后对所有SNP位点的信息素值乘以损失率r_loss来蒸发一定量的信息素;
步骤3每隔一定迭代次数(本文为每1 000次)禁忌信息素最高的一个SNP位点,当迭代次数达到最大迭代次数genmax后,终止算法循环。
1.3 基因型数据的数字表示,双位点组合的逻辑关系及适应度函数的计算
在1.2节所述的算法流程中,适应度函数用来刻画基于某一双位点组合状态将全体病例分组的组间眼压差异。双位点组合把所有对象划分为阳性组(即该组眼压各项统计参数偏高)和阴性组,这两组的眼压平均值之差越大表明这个双位点组合对眼压预测的意义越显著。
对于确定的每个双位点组合都有9种基因型及4种布尔逻辑运算关系。每一个SNP位点的碱基构成可以分为3类,即常见纯合子(AA)、罕见纯合子(aa)以及杂合子(Aa),故两个位点的组合有9种可能的基因型。考虑了两个位点之间的4种布尔逻辑运算[10],即:
AND 当且仅当第一个SNP取特定值并且第二个SNP取特定值时,个体是阳性的;
OR 当且仅当第一个SNP或第二个SNP取特定值时,个体是阳性的;
AND NOT 当且仅当第一个SNP取特定值,且第二个SNP不取特定值时,个体是阳性的;
XOR 当且仅当两个SNP中的一个具有特定值而另一个SNP不采用特定值时,个体是阳性的。
当给定了基因型组合和逻辑关系后,可以把样本眼压划分为两组,从而计算适应度函数值。9种基因型组成和4种逻辑关系形成36种组合方式,故可得到36个适应度函数值,取这36个值中的最大值作为该双位点组合最终的适应度函数值。本文算法使用的适应度函数为
(2)
式中,Mp表示阳性一组的人数;Pp表示阳性一组的眼压平均值;Mn表示阴性一组的人数;Pn表示阴性一组的眼压平均值;Pm表示所有受测试者的眼压平均值。
2 实验部分
2.1 实验数据及处理
利用本文的蚁群算法分析了来自EBI的澳洲人群青光眼患病情况调查数据。该数据包含2 627个合格受测试者样本(未测到眼压值的不合格样本有134个),在594 398个SNP位点上的基因数据和眼压值。基因数据按其所在不同染色体位置划分为26个子数据(1~22、XY、X、Y、MT,XY表示X染色体和Y染色体的重叠部分,MT表示线粒体),数据表每行记录一个SNP位点的信息,前5列记录该位点编号、所在位置和碱基成分,之后每3列对应一个受测试者是显性纯合子、杂合子或隐性纯合子的概率。最终的输入数据是一个594 398×2 627的基因数据矩阵和一个2 627×1的眼压数据矩阵。
2.2 蚁群算法的参数设置
首先用包含8 713个位点的21号染色体进行预实验,来选取算法的核心参数(蚂蚁数)。计算21号染色体上任意双位点组合的适应度函数值,并按该值降序排列这些组合,前750个组合具有统计显著性。接下来,在其他参数相同的条件下只改变蚂蚁数,把计算结果中属于这750个位点对的个数作为评价算法计算效率的标准。在预实验中,将蚂蚁数分别设置为10、20和30,竞赛规模都设置为20,迭代次数分别设置为300 000、150 000、100 000次(确保算法总的计算次数相同)。图1展示了在不同蚂蚁数下,随着计算次数增加蚁群算法在预实验子集上能搜索到的前750位组合个数。
从图1中可以看到,蚂蚁数目设置为20时,蚁群算法搜索到的关键位点对个数最多。所以在接下来的全位点实验中将蚂蚁数恒定地取为20,同时将竞赛规模设置为20。另外,每1 000次迭代禁忌一次位点。
2.3 全部位点蚁群实验结果
在全位点实验中使用的计算机包含参数为Intel i7- i7- 6850K的CPU,2 400 MHz的32G内存以及Ubantu 14.04的操作系统。根据计算机性能将算法的最大迭代次数设置为800 000次。完成本文设计的蚁群算法的800 000次迭代总共用时220 h。表1列出了秩和检验P值最小的10个双位点组合。在所有结果中,有6对双位点组合的秩和检验P值小于1×10-4,秩和检验P值小于1×10-2的一共有137对结果。
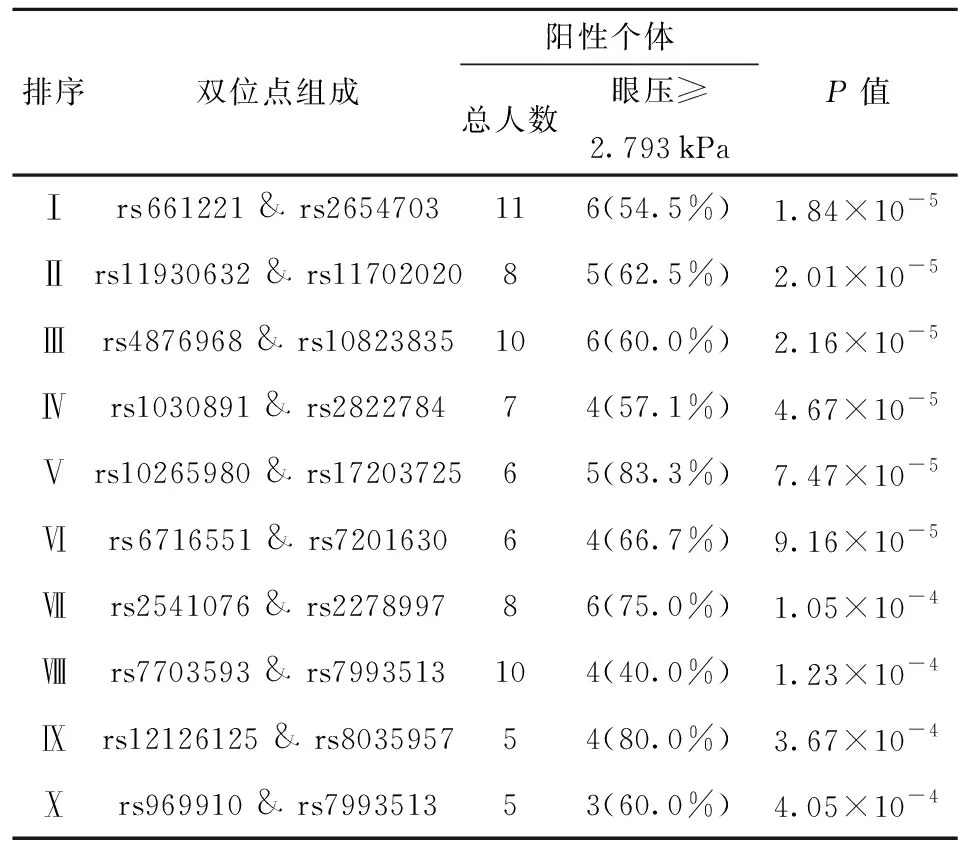
表1 秩和检验P值最优的前十组双位点组合Table 1 Top ten optimal combinations of SNPs of rank sum test P-value
括号内数字为满足条件的人数占总人数的比例。
在之前关于青光眼数据的眼压与单位点研究中,得到与该疾病显著相关的一个单位点是位于17号染色体基因GAS7上的rs11656696[9],在本文所分析的EBI数据集上该位点的秩和检验P值为5.03×10-2。本文所发现的双位点组合对于眼压预测的秩和检验P值低于该单位点的秩和检验P值,也即我们发现的双位点组合对眼压的影响更具有统计显著性。
本文实验中,秩和检验P值最小的组合是位点rs661221与rs2654703,该组合的秩和检验P值为1.84×10-5,且这个位点对划分得到的阳性组和阴性组的眼压样本均满足正态分布。
进一步计算了位点rs661221与位点rs2654703的T检验P值,为6.9×10-12,显著优于文献[9]。位点rs661221位于1号染色体的基因RIMS3上,位点rs2654703位于3号染色体的基因FGF12上。另外,从表1可以看到,P值最小的10组双位点组合划分出的阳性组中,眼压高于2.793 kPa的病例比例明显高于普通人群中的比例,而眼压高于2.793 kPa在临床上是青光眼发病的重要指征。这表明本文算法发现的双位点组合与青光眼发病因素显著相关。
图2(a)展示了秩和检验P值小于1×10-2的结果在染色体上分布的热图,图中色块的灰度深浅代表位点对的多少。横纵坐标为位点所在染色体位置编号(1~21),组成位点分别位于横纵坐标标示的染色体上。图2(b)是将图2(a)的内容反映在点和边上的分布图,图中节点度数代表两位点在同一染色体的结果个数,有2对双位点组合的组成位点都在2号染色体上;3号和11号染色体各有1对双位点组合的组成位点都在同一染色体上;其余染色体不包含双位点组合的组成位点都位于同一染色体的情况。图2(b)中连接各节点的边的粗细代表组成双位点组合的各位点分别位于两不同染色体的组合个数。如图2(b)所示,最粗的一条边(染色体之间双位点组合最多)在1号染色体和3号染色体之间,包含8对双位点组合;其次为2号染色体和6号染色体之间的边,包含6对双位点组合。
图2表明,137对显著双位点组合涉及2号染色体的个数最多,因此对涉及到2号染色体位点的所有结果进行了分析,发现2号染色体基因LOC107985962上的位点与其他11个染色体上的位点组成了显著性较高的组合。其中包括位点rs7742590,该位点与基因FOXC1都位于6号染色体,且距离基因FOXC1大约1 600万个碱基。据文献[12]报道,6号染色体上基因FOXC1被怀疑与POAG发病高度相关。
如表2所示,11个双位点组合都包含2号染色体基因LOC107985962上的位点。以上位点中有5个位于明确的基因上,在这5个基因中,有两个基因的功能已被确认(分别为ERICH6- AS1和PDE8B),其余3个基因的功能尚未被确认。ERICH6- AS1属于RNA反转录基因,PDE8B属于磷酸二酯酶调控基因。根据美国国家生物技术信息中心(National Center for Biotechnology Information,NCBI)数据库上收录的常规组织表达量数据,以上两个基因都在胎盘组织具有一定表达量。因此可以猜测该基因通过基因间相互作用影响其他基因的表达,从而引起胎儿的先天性青光眼。本文所提蚁群算法选取的双位点组合与生物医学已经证实的结果具有较高的相合性。本文结果的生物学意义有待通过进一步的生物实验来验证。

表2 与位点rs13414786相关的双位点组合Table 2 Site pair combinations involving SNP rs13414786
3 结论
本文的研究提供了一种通过探索连续型变量与多位点组合的关联性来发现与疾病相关的SNP组合的新思路。通过10 000位点子集的实验找到了合理的参数,提高了所设计算法的计算效率,同时也增强了算法对边际效应较高双位点组合的探索能力。另外,通过全部位点的实验,在2号染色体上找到了一系列未被报道的显著性水平较高的位点组合,这些位点组合很有可能通过医学实验得到进一步证实,从而为探索与眼压相关的基因功能和青光眼的发病原理提供新的线索。

