一种分形晶格上Potts模型的相变

尹训昌

（安庆师范大学,安徽安庆246133）

0 引言

相变问题一直是热力学统计物理中的一个研究热点，在教材中主要介绍一维和二维正方晶格Ising模型的相变。教材中的正方晶格满足平移对称不变性，且它们的空间维数仅能取正整数。分形晶格不具有平移对称特点，分形维数可以是非正整数，因此，讨论分形晶格上自旋模型的相变有一定的理论意义。分形是一种具有高度自相似特性的几何图形，分形维数和分岔度是分形的两个重要参数。20世纪80年代初，Gefen等人讨论了几种分形晶格上Ising模型的相变问题［1］，得到了无外场下系统的临界点。从此以后，分形晶格上自旋系统的相变得到了越来越多的重视［2-7］。前人关于Potts模型的工作主要集中在可以约化的分形晶格，而本文所讨论的分形晶格是不能约化的，它更加接近自然界中的真实铁磁系统。本文应用实空间重整化群的方法，讨论一种不可约化的分形晶格上Potts模型的相变问题。

1 一种分形晶格和Potts模型

图1 描述了本文所讨论的分形晶格的生成过程。该分形是通过连续迭代形成的，首先选取一个由两个点和一个键组成的图形作为最基本单元（即n=0级），再取八个最基本单元构成一个图形，为了简单我们称之为生成元（n=1级），最后把生成元作为一个整体替换生成元中的每个键。最后一个步骤重复无穷多次，就得到不可约化的分形晶格。容易得知，该分形晶格的分形维数表示为d f=ln 8/ln 2=3，其分岔度为无穷。对于该分形晶格，每个格点的配位数不相同，它与格点的位置密切相关，因此它属于一种典型的非均匀晶格。该分形晶格上Potts模型的有效哈密顿量为：

其中，K用来描述约化的最近邻相互作用参数，符号si和sj分别用来表示格点i和j位置上的离散自旋变量，它只能取1,2两个整数值，＜sisj＞代表只对最近邻之间的自旋求和，δ为克罗内克delta记号。该系统的配分函数可以写为：

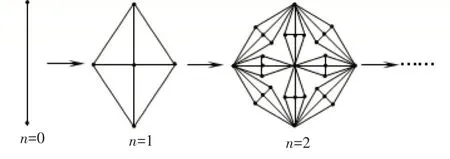
图1 一种分形晶格的生成过程

2 重整化群变换过程

为了便于表述，选取生成元进行重整化群变换。图2（a）为该晶格的生成元，不同格点位置上的自旋分别用sa，sb，s1，s2和s3来表示。根据（1）式，写出该生成元的有效哈密顿量如下：

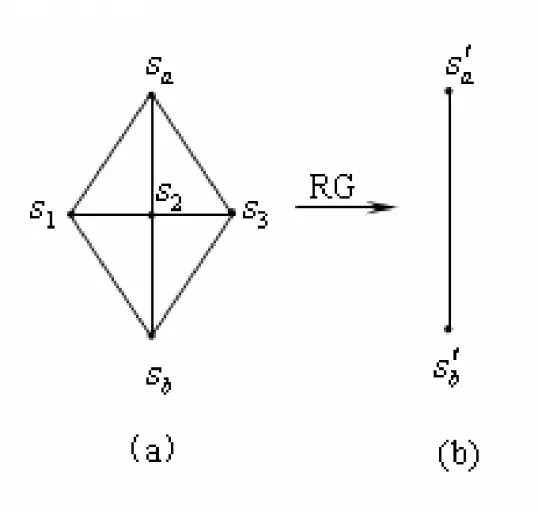
图2 重整化群变换过程

经过一次重整化群变换后，图2（a）内部的3个格点被消去变为图2（b），这个步骤表示为：

其中，P只表示一个仅与积分有关的重整化群常数，H′表示经过重整化群变换后图2（b）的有效哈密顿量，它的表达式写为：

把（3）式和（5）式代入（4）式，通过推导得到重整化群变换后的关系式为：

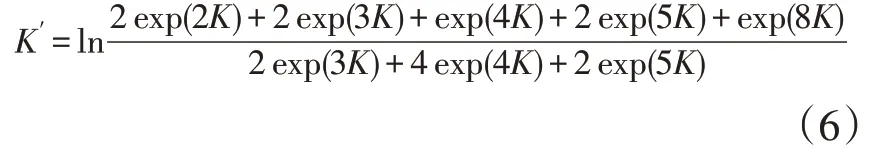
（6）式称为该分形晶格上Potts模型相变的递推关系。

为了求得该系统的临界点，假设K′=K=K∗，由（6）式通过计算得到该系统的临界点为：

为了计算关联长度的临界指数，在临界点附近区域把递推关系进行线性如下变换:

3 结论

本文采用实空间重整化群变换方法，研究了一种不可约化的分形晶格上Potts模型的相变，求得了该系统的临界点和表征关联长度性质的临界指数。结果表明，该分形晶格上的Potts模型在K∗=0.528发生相变，通过进一步分析可知该相变温度为有限值。与该分形晶格上的Ising模型进行比较，发现该系统的临界点在数值上产生了明显的变化。