可公开验证无证书的多接收者匿名签密方案

陈 虹，朱亚囡，肖成龙，金海波，张子浩

辽宁工程技术大学 软件学院，辽宁 葫芦岛125105

1 引言

公钥加密和数字签名往往需要很大的计算开销，将两者结合起来相较于独立使用两个算法，不仅能更快速的计算，而且消息扩展也更短，提高了效率，避免了资源浪费。1997年，Zheng[1]首次提出签密的概念，签密能够在一个步骤内同时实现签名和加密，其优越性吸引众多研究人员关注，逐渐将签密思想和现实的应用需求结合起来，提出很多具有特殊属性的签密方案[2-6]。为了满足广播环境下发送者同时发送消息给多个接收者的需求，2006年，李大兴等[7]提出了一个发送者对应多个指定接收者的签密方案，方案利用超奇异椭圆曲线上Tate对的特性，仅需一次加密，就能发送给多个接收者，提高了传输消息的效率，节省了资源。自此出现了很多多接收者签密方案，然而方案生成的密文中往往包含发送者的身份或密文标记列表，致使多接收者签密方案[8-13]密文泄露接收者的身份，为了解决接收者身份信息泄露的问题，2014 年，庞辽军等[14]提出一种基于身份的多接收者匿名签密方案，使用用户的身份标识来生成公钥，并将接收者的身份利用拉格朗日插值隐藏起来，使得解密时能够验证用户身份的合法性，却无法得到用户的真实身份，且每个用户可以验证密文的有效性，保护了用户的隐私，但该签密方案私钥是由密钥生成中心（Key Generation Center，KGC）生成，面临PKG 恶意泄露私钥信息的情况，为了解决这一问题，研究人员提出了基于无证书体制的多个接收者的签密方案，用户和KGC 组合生成密钥，因此KGC无法获得用户完整的私钥，解决私钥泄露的风险。2015年，于志敏等[15]提出一种基于多线性映射的多接收者签密方案，在无证书体制下采用多个一级编码相乘的方法，将方案的求解难度提升到了求解一个基于多级计算性Diffie-Hellman 问题，提高方案的安全性，但该公钥尺寸大，且方案计算繁琐，实用性不高。2016年，周彦伟等[16]提出一种无证书多接收者多消息签密机制，该方案使用索引定位的方法标识密文，对接收到的密文需每个接收者各自定位到相应的密文，再去使用各自私钥去解密，解密效率提高，但该方案操作复杂且容易暴露接收者的身份；2017 年，秦艳琳等[17]提出一种无双线性对的无证书多接收者匿名签密方案，该方案采用拉格朗日插值方法来隐藏接收者身份，且在签密过程中没有使用双线性对，降低了计算开销，然该方案被证明未真正实现接收者身份匿名性。

针对上述方案的不足，在随机预言模型下提出一种可公开验证的无证书多接收者匿名签密方案，该方案解决了发送者身份模糊、接收者身份泄露的问题，且计算量适中，适合实际应用。本文首先介绍了方案的预备知识，然后提出了一种新的多接收者签密方案，在随机预言模型下证明了该方案的机密性、不可伪造性和可公开验证性，最后与现有的一些多接收者签密方案相比，证明本文方案所采用的方法更加的安全高效。

2 预备知识

2.1 双线性映射

2.2 困难性问题

3 签密方案

3.1 多接收者匿名签密方案的构成

多接收者签密由KGC、发送者和接收者三方构成，方案有以下几个步骤。

（1）系统初始化算法：此算法是由KGC 来完成的，首先将系统的安全参数k 输入进去，对应输出主密钥s 和参数params，其中主密钥s 秘密保留，参数params公开。

（2）用户密钥生成算法：首先输入参数params、主密钥s 和用户的身份ID，由KGC 输出用户的部分私钥DID，用户自己选取一个秘密值xID，将两者结合起来生成完整的私钥SKID，然后用户输入参数params 和身份ID，输出用户的部分公钥，再由用户秘密值和生成元计算出的值作为公钥的另一部分，由此生成完整公钥。

3.2 本文多接收者签密方案的构成

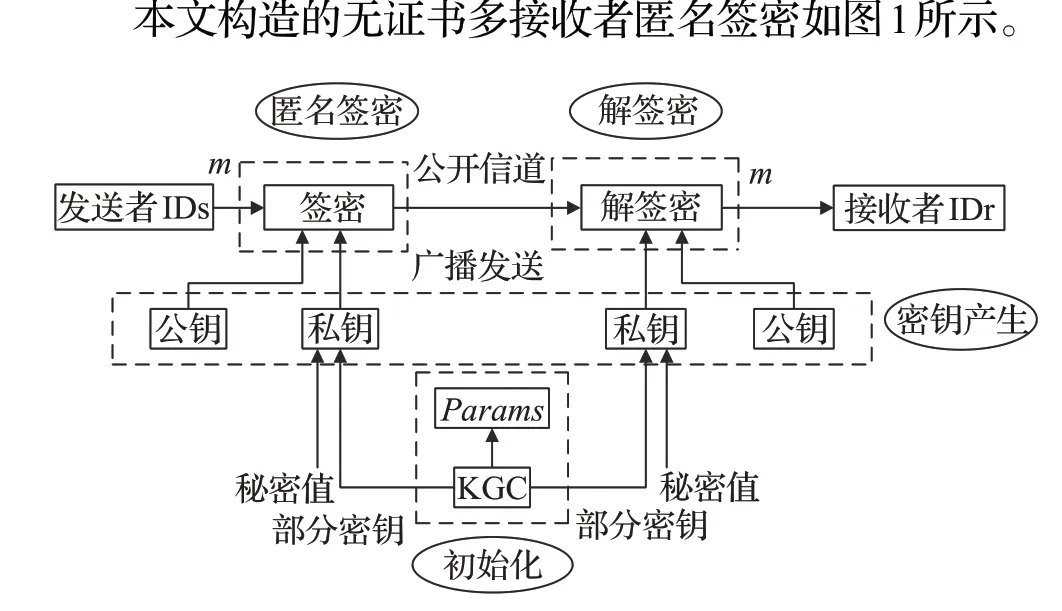
图1 无证书多接收者匿名签密方案

3.3 正确性证明

方案的正确性分析主要包括密钥正确性、密文的可恢复性和发送者合法性、签名正确性等分析，具体如下：

（1）密钥正确性

用户的密钥由KGC 和用户手中的部分密钥组成，为了保证KGC 传来的密钥的可靠性，可以通过以下公式验证KGC传递的部分私钥的正确性：

4 安全模型

签密的安全目标是对通信数据提供认证性和保密性。安全性可以根据敌手的不同，分为外部安全（只知道公共信息）和内部安全（合法用户）。本章从机密性（选择密文攻击下的不可区分性，IND-CCA2）和认证性（选明文攻击下不可伪造性，sUF-CMA）来定义内部安全性和外部安全性，通常可以通过KGC 和敌手之间的相互交互来验证，参照文献[13]的定义，利用四类游戏（游戏一、游戏二、游戏三、游戏四）来模拟方案受两类敌手攻击的过程，第一类敌手是恶意的用户，可以无条件更换用户的公钥，但无法得知系统的主控钥；第二类敌手是恶意的KGC，掌握着系统的主控钥，但无法更换用户的公钥。两类敌手和KGC中的算法之间的交互如图2和图3所示。

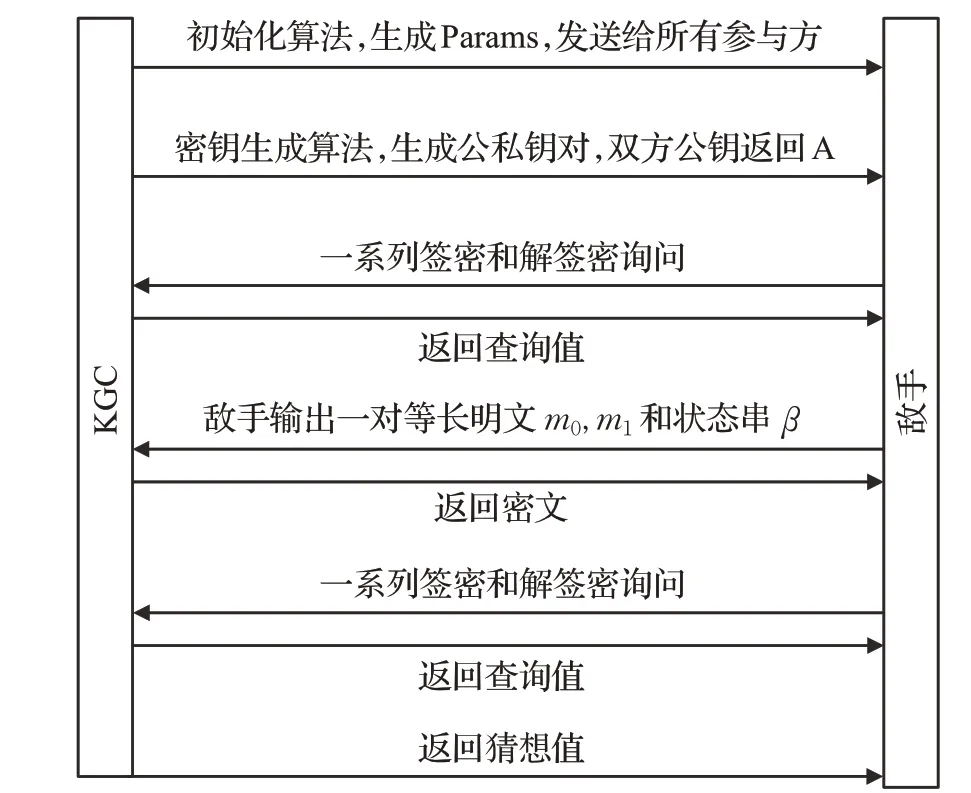
图2 适应性选择密文攻击模拟图

图3 选择消息攻击模拟图

4.1 机密性分析

4.2 不可伪造性分析

定义4（类型二攻击下的不可伪造性）若在固定时间t内敌手SUF-CCA2 赢得游戏一优势ε‴是可以忽略不计的（执行qe次密钥询问，qs次签密询问，qd次解签密询问和q1,q2,q3,q4次对哈希函数H1,H2,H3,H4的询问），则有算法B 能够在t′≤t内，以优势ε*≥ε‴/2-qs/2k+1解决DL问题。

证明证明过程与定义3类似，此处不再论证。

5 性能分析

从计算效率和安全属性上对方案进行分析，计算效率主要取决于多接收者匿名签密和签密验证算法的计算量。因为散列函数和点加运算所用的时间远小于其余的计算时间，可以忽略不计，因此计算量主要统计双线性对、点乘和指数运算的执行次数，分别用E、P、M表示指数运算、双线性对运算和点乘计算，一个双线性对约等于20 个点乘，一个指数约等于3 个点乘，将本文方案和其他类似方案进行比较，结果如表1和表2所示。

表1 多接收者签密计算效率

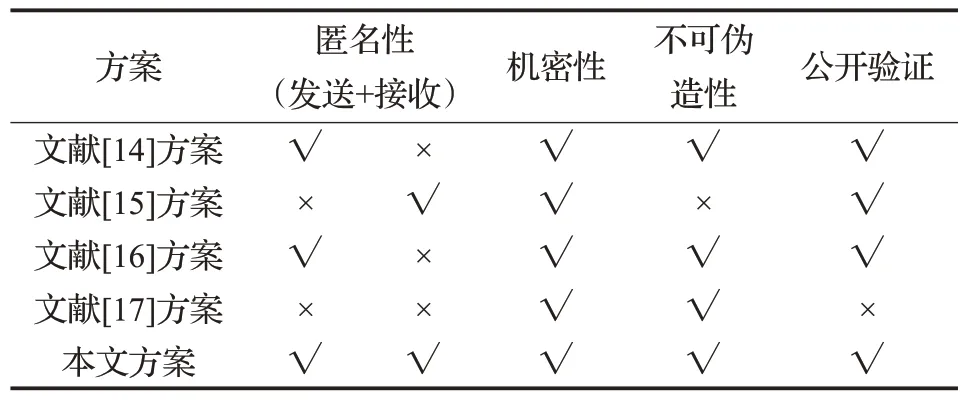
表2 多接收者签密安全属

从表1可以看出文献[16]在计算开销上存在明显的优势，但该方案使用的是索引定位的方法来确定接收者所属的密文，需找到准确密文后再进行解密，操作复杂，且此段开销并未计算进去；本文与文献[15]相比，文献[15]不使用双线性对，计算开销也较小，但随着接收者增多，开销增长的幅度相比本文也会加大；本文与文献[17]相比，在随着接收者增加的趋势下有着相近的增长幅度。

从表2可以看出，文献[14]、[16]和[17]相比，本文方案具有接收者匿名性，能解决接收者身份泄露的问题；本文与文献[15]和[17]相比，能实现发送者身份匿名性，确保发送者身份不被泄露；本文与文献[17]相比，本文具有可公开验证性，能够确保密文的有效性和发送者身份的合法性。本文方案与其他文献相比安全性更高、更全，适用于网络组播中的签密服务、云中的数据共享以及网络会议等领域。

6 结束语

针对多接收者签密方案发送方和接收方身份泄露的问题，采用哈希函数和多项式将身份隐藏起来，保护了用户的隐私，实现身份的匿名性，且方案可公开验证密文有效性。然而方案在注重抗攻击性能时，计算开销就会有所忽略，因此平衡方案的运行效率和抗攻击性能，仍是以后研究的重点。