单粒子未知态的分级量子通信

雷 佳, 柏明强, 周思齐, 廖 婷

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

量子纠缠是量子力学的核心,并且在量子信息处理中扮演着重要的角色.几乎所有的量子通信任务都离不开量子纠缠,如量子隐形传输、量子稠密编码、量子克隆、远程态制备、量子秘密共享等.其中,量子秘密共享指的是发送者将一个量子秘密通过一定的方式拆分,然后将拆分后的量子秘密发送给不同的接收者,只有部分或所有接收者共同合作才能恢复最初的量子秘密信息.1999年,Hillery等[1]提出了基于GHZ态的量子秘密共享方案.随后,人们又陆续提出利用Bell态、W态、Cluster态及多粒子纠缠态等作为量子信道的量子秘密共享方案[2-9].量子秘密共享又被叫做量子信息分离.

最初的量子信息分离方案对于量子信息分离都是对称的,即接收者都需要其他所有的接收者协助才能恢复量子秘密,那么有没有只需要一部分接收者协助就能恢复发送者的秘密呢？文献[10-12]提出了分级量子分离方案.在该方案中,具有多名接收者,不同的接收者对量子信息的恢复能力不同.根据接收者对未知态的恢复能力,将他们分为2个等级.高级接收者只需要部分接收者协助就可以恢复发送者的未知态,低级接收者需要所有的接收者合作才能重构发送者的未知态.2013年Bai等[13]提出了以8粒子Cluster态作为量子信道的分级量子信息分离方案,2014年王作栋等[14]提出了二粒子分级量子信息分离方案,Peng等[15]提出了利用4粒子非最大纠缠态分级量子信息分离方案.

以上的分级量子信息分离方案,都是将接收者分为2个等级,那么能不能将接收者分为3个等级呢？于是本文提出了利用一个4粒子Cluster态和一个3粒子GHZ态[16-17]作为量子信道,实现任意单粒子未知态的三级量子通信方案.发送者Alice将单粒子未知态分发给6个接收者,接收者对未知态的恢复能力不同,其中,Bob只需要2个接收者协助就可以恢复Alice发送的未知态,Charlie1(Charlie2)需要3个接收者的协助才可以恢复Alice发送的未知态,David1(David2、David3)需要4个接收者协助才可以恢复Alice发送的未知态.

1 分级量子通信

假设Alice有一个单粒子未知态,形式为

|φ〉x=α|0〉x+β|1〉x,

(1)

其中,α、β是复数并满足|α|2+|β|2=1.Alice作为分级量子通信中的发送者,发布一个秘密态|φ〉x给6个接收者,他们之间的量子信道由一个4粒子Cluster态和一个3粒子GHZ态构成.

|1100〉-|1111〉)1234,

(2)

其中，粒子x和1属于Alice,粒子2属于Bob,粒子3和4分别属于Charlie1和Charlie2,粒子5、6、7分别属于David1、David2、David3.此时系统总态为

|ψ〉x1234567=|φ〉x⊗|C4〉1234⊗|G〉567=

|011000〉+|011111〉)+

α|01〉(|100000〉+|100111〉-

|111000〉-|111111〉)+

β|10〉(|000000〉+|000111〉+

|011000〉+|011111〉)+

β|11〉(|100000〉+|100111〉-

|111000〉-|111111〉)]x1234567.

(3)

Alice向6个接收者发送一个秘密态|φ〉x使任何一个接收者在部分或全部接收者的帮助下都能重构这个秘密态.为了达到这个目的,Alice首先对其两粒子执行Bell测量{|Ψ±〉x1,|Φ±〉x1},然后通过经典信道将测量结果发送给接收者,其中,4种Bell基为

|Ψ±〉

|Φ±〉

(4)

Alice执行Bell测量之后,系统的塌缩态为|ψ±〉234567或|φ±〉234567,其中

|ψ±〉234567=x1〈Ψ±|ψ〉x1234567=

|011000〉+|011111〉)234567±

|111000〉-|111111〉)234567,

|φ±〉234567=x1〈Φ±|ψ〉x1234567=

|111000〉-|111111〉)234567±

|011000〉+|011111〉)234567.

(5)

1.1选择Bob恢复秘密假设Alice选择让Bob来恢复秘密态.首先,Bob和David1联合以粒子5为控制粒子,粒子2为目标粒子执行受控非门,然后系统塌缩态变成如下形式：

|011000〉+|111111〉)234567±

|111000〉-|011111〉)234567,

|111000〉-|011111〉)234567±

|011000〉+|111111〉)234567.

(6)

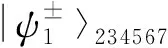
β|1〉2)|00000〉234567+

β|0〉2)|00000〉234567+

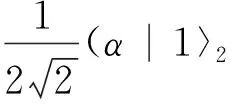
(7)

为了帮助Bob重建最初的秘密态,其他接收者选取合适的测量基对他们自己的粒子进行测量，并公布他们的测量结果.通过(7)式,很显然,如果Charlie1和Charlie2选取{|0〉,|1〉}对他们的粒子进行测量,他们的测量结果总是相同的.同样的,David1、David2和David3也选取{|0〉,|1〉}对自己的粒子进行测量,他们的结果也是相同的.因此只需要Charlie1和Charlie2中的任意一个和David1、David2和David3中的任意一个将测量结果发送给Bob,Bob通过相应的幺正操作就可以重构初始未知态,从而实现秘密恢复,完成本次量子通信.

不失一般性,假设Alice、Charlie1和David1的测量结果分别为|ψ+〉x1、|0〉3和|1〉5,则Bob得到的测量结果为

|ψ〉2=β|0〉2-α|1〉2.

(8)

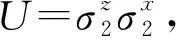
|ψ1〉2=α|0〉2+β|1〉2.

(9)

对于该方案的所有可能的详细测量结果,测量后的塌缩态,Bob需要做的幺正变换见表1.

表 1 Alice、Bob、Charlie1和David1的测量结果,Bob手中粒子的塌缩态及所做的幺正操作

注：表中I为单位算子,σx=|0〉〈1|+|1〉〈0|,σz=|0〉〈0|-|1〉〈1|和σy=i|1〉〈0|-i|0〉〈1|为常见的Pauli算子,下同.

1.2选择Charlie1恢复秘密因为|φ〉x1234567在交换粒子3、4的顺序时是不会改变的,所以Charlie1和Charlie2在这个协议中具有相同的地位.不妨考虑让Charlie1来恢复Alice的秘密态|φ〉x,Charlie1首先以粒子5为控制粒子,粒子3为目标粒子做受控非门,然后以粒子2为控制粒子,粒子3为目标粒子做受控非门,然后对粒子2做Hadamard门变换,则|ψ±〉234567和|φ±〉234567变为如下形式

β|1〉3)|ξ1〉24567+

(α|1〉3±β|0〉3)|ξ2〉24567+

(α|0〉3∓β|1〉3)|ξ3〉24567+

(α|1〉3∓β|0〉3)|ξ4〉]24567,

β|0〉3)|ξ1〉24567+

(α|0〉3±β|1〉3)|ξ2〉24567+

(α|1〉3∓β|0〉3)|ξ3〉24567+

(α|0〉3∓β|1〉3)|ξ4〉]24567,

(10)

其中

|ξ1〉=(|00000〉+|11111〉)24567,

|ξ2〉=(|00111〉+|11000〉)24567,

|ξ3〉=(|10000〉+|01111〉)24567,

|ξ4〉=(|10111〉+|01000〉)24567.

从(10)式可以知道,如果David1、David2和David3选择{|0〉,|1〉}对自己的粒子进行测量,他们的测量结果是一样的,因此Charlie1只需要得到Bob、Charlie2和David1(David1或David1)的测量结果并做相应的幺正操作即可恢复Alice的量子态信息.换句话说,Charlie2只需要其他5个接收者中的3个就可以恢复Alice的量子态秘密.完成本次量子通信.不失一般性,假设Alice、Bob、Charlie2和David1的测量结果分别为|φ-〉x1、|0〉2、|1〉4和|1〉5,则Charlie1获得的测量结果为

|φ〉3=α|1〉3-β|0〉3.

(11)

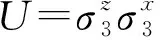
|φ1〉3=α|0〉3+β|1〉3.

(12)

对于该方案的所有可能的详细的测量结果,测量后的塌缩态,Charlie1需要做的幺正变换见表2.

1.3选择David3恢复秘密因为|φ〉x1234567在交换粒子5、6、7的顺序时是不会改变的,所以David1、David2和David3在这个协议中具有相同的地位.考虑另一种情况,所有接收者都同意让David3来恢复Alice的秘密态|φ〉x,David3首先以粒子2为控制粒子,粒子6和粒子7为目标粒子做受控非门,然后对粒子2和6做Hadamard门变换,则|ψ+〉234567和|φ±〉234567变为如下形式：

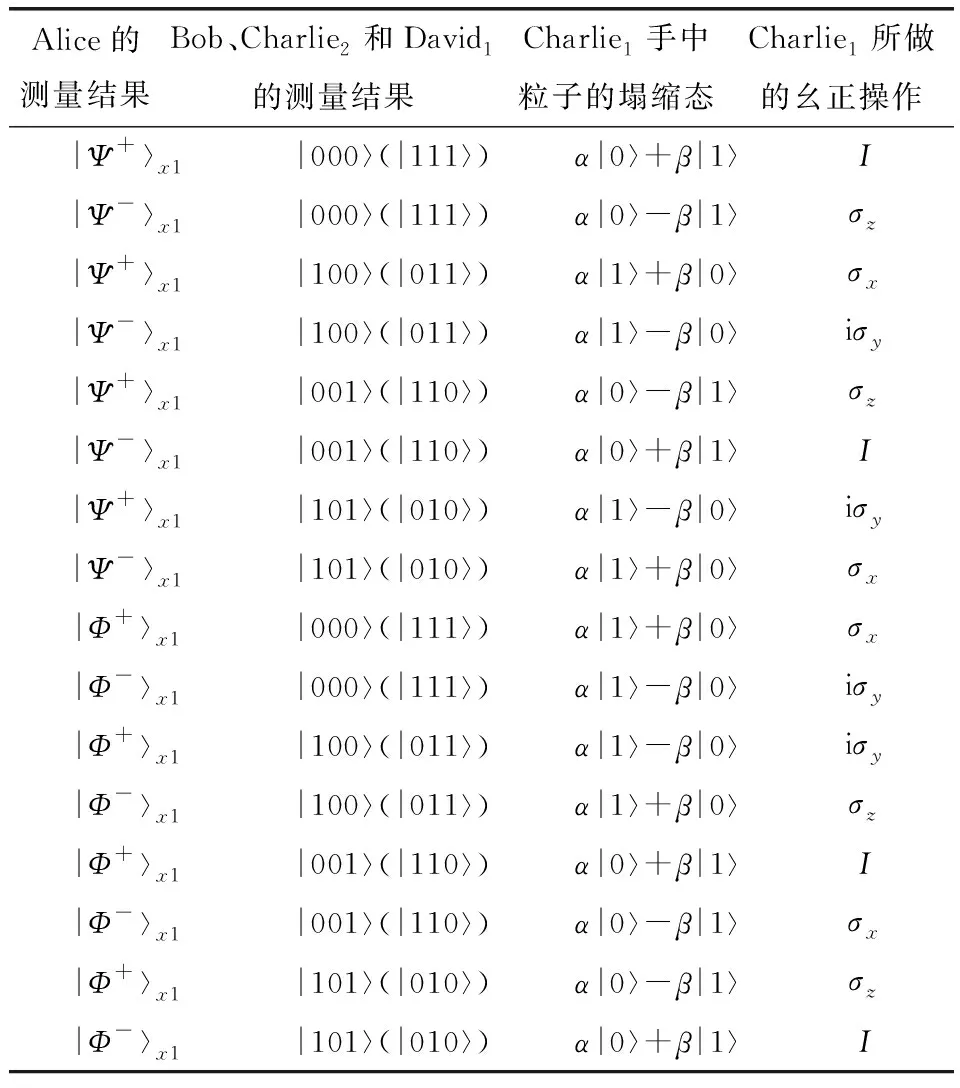
表 2 Alice、Bob、Charlie2和David1的测量结果,Charlie1手中粒子的塌缩态及所做的幺正操作

β|1〉7)|φ1〉23456+

(α|0〉∓β|1〉)|φ2〉23456+

(α|1〉7±β|0〉7)|φ3〉23456+

(α|1〉7∓β|0〉7)|φ4〉]23456,

β|0〉)7|φ1〉23456+

(α|1〉∓β|0〉)|φ2〉23456+

(α|0〉7±β|1〉7)|φ3〉23456+

(α|0〉7∓β|1〉7)|φ4〉]23456,

(13)

其中

|φ1〉=|00000〉+|10001〉+|11100〉+|01101〉23456,

|φ2〉=|00001〉+|10000〉+|01100〉+|11101〉23456,

|φ3〉=|00010〉+|10011〉+|01111〉+|11110〉23456,

|φ4〉=|00011〉+|10010〉+|11111〉+|01110〉23456.

通过(13)式,David3重构Alice的秘密态需要其他接收者分别对自己的粒子做单粒子测量,并将测量结果通过经典信道发送给David3.由(13)式可知,Charlie1和Charlie2选取{|0〉,|1〉}对他们的粒子进行测量,他们的测量结果总是相同的,因此,只需要他们中的一个协助David3.也就是说,David3需要Bob、Charlie1(Charlie2)、David1和David2共4个接收者的帮助就可以重构发送者的未知态,恢复量子秘密,完成本次通信.一旦他们的测量基被确定,整个系统塌缩态为下面4种形式:

α|0〉7±β|1〉7,α|1〉7±β|0〉7,

α|0〉7∓β|1〉7,α|1〉7±β|0〉7,

(14)

当David3得到形如(14)式的塌缩态时需要做的合适的幺正操作如表3.

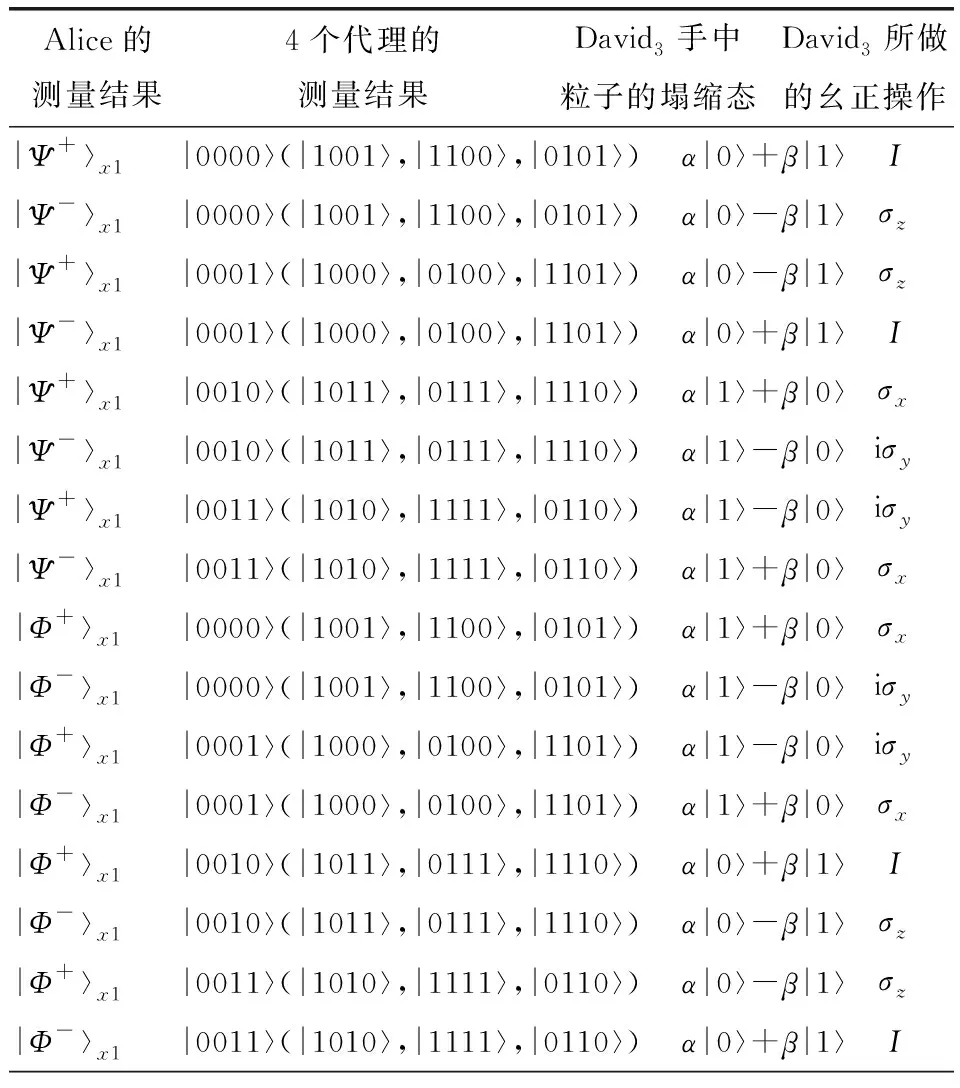
表 3 Alice、Bob、Charlie2、David1和David2的测量结果,David3手中粒子的塌缩态及所做的幺正操作

2 安全性分析

下面从外部攻击和内部攻击2个方面对本方案进行安全性分析.假设有一个偷窃者叫Eva,其在粒子的分配过程中通过纠缠一个辅助粒子来盗取Alice准备发送的量子态信息.如果Alice和接收者们都没有发现偷窃者Eva,那么在Alice对自己的粒子进行Bell测量后,接收者们和偷窃者Eva构成的量子系统将塌缩为7粒子纠缠态,然而,在协助接收者对自己的粒子进行单粒子测量后,恢复秘密的接收者和Eva所构成的系统将塌缩为一个直积态,因此Eva不会获取到任何信息.为了更清楚地阐述,假设Eva试图利用辅助粒子|0〉8纠缠Alice和接收者们的纠缠信道.如果Alice的测量结果为|ψ+〉x1,接收者和Eva所构成的纠缠态为

|0110000〉+|0011110〉)2345678±

|1010000〉-|1111110〉)2345678.

(15)

当Charlie1和David1分别选取基|0〉3和|1〉5对自己的粒子进行测量,Bob和Eva的混合态将塌缩为β|00〉28-α|10〉28.很显然,Eva的态并没有改变,由纠缠的对应特性,在这次攻击中Eva并没有窃取到任何的量子态信息.

考虑另一种攻击情况,假设接收者中有一方是不诚实的,即Bob是不诚实的.他想安全独立的恢复Alice的秘密.为了达到这个目的,Bob通过拦截Alice发送给其他接收者的信道粒子,然后将自己事先准备好的辅助粒子发送给其他接收者.在这种情况下,只有当Alice选择Bob恢复量子态信息,Bob可以成功地重构未知态并避免安全检测.但如果Alice选择除了Bob以外的其他接收者恢复量子态信息,那么其他接收者重构的未知态将不同于Alice发送的.当他们进行公开比较时,窃取行为将会被发现.因此,在整个共享过程中Bob成功的概率只有16.67%.如果检查态的量足够大,那么非法用户Bob将会被发现.

综上所述,对于某些窃取者的攻击本分级量子信息分离是安全的.

3 结论

本文探讨了利用一个4粒子Cluster态和一个3粒子GHZ态作为量子信道实现单粒子未知态的分级量子通信方案.在该方案中,Bob只需要2个接收者协助就可以重构发送者的未知态,而Charlie1和Charlie2都需要3个接收者的帮助就能恢复发送者的未知态,David1、David2和David3需要4个接收者协助才能恢复未知态,也就是说,Bob比其他的接收者更容易恢复发送者的秘密,David1、David2和David3比其他接收者更难恢复发送者的秘密.换句话说,6个接收者的权限被分为3个等级,Bob作为高级接收者,Charlie1、Charlie2为中级接收者,David1、David2和David3为低级接收者.也可以修改方案实现(2,3)阈值的受控分级量子信息分离.

[1] HILLERY M, BUZEK V, BERTHIAUME A. Quantum secret sharing[J]. Physical Review,1998,A59(3):1829-1834.

[2] LI X H, PING Z, LI C Y, et al. Efficient symmetric multiparty quantum state sharing of an arbitrarym-qubit state[J]. J Physics:Atomic Molecular Optical Physics,2005,B39(8):1975-1983.

[3] DENG F G, LI X H, LI C Y, et al. Multiparty quantum state sharing of an arbitrary two-particle state with Einstein-Podolsky-Rosen pairs[J]. Physical Review,2005,A72(4):044301.

[4] KARLSSON A, KOASHI M, IMOTO N. Quantum entanglement for secret sharing and secret splitting[J]. Physical Review,1999,A59(1):162-168.

[5] ZHENG S B. Splitting quantum information via W states[J]. Physical Review,2006,A74(5):054303.

[6] MURALIDHARAN S, PANIGRAHI P K. Quantum information splitting using multi-partite cluster states[J]. Physical Review,2008,A78(6):062333.

[7] HOU K, LI Y B, SHI S H. Quantum state sharing with a genuinely entangled five-qubit state and Bell-state measurements[J]. Optics Communications,2010,283(9):1961-1965.

[8] LI Y H, LIU J C, NIE Y Y. Quantum information splitting by using a genuinely entangled six-qubit state and Bell-state measurements[J]. Acta Photonica Sinica,2011,40(2):307-310.

[9] NIE Y Y, LI Y H, LIU J C, et al. Quantum information splitting of an arbitrary three-qubit state by using two four-qubit cluster states[J]. Quantum Information Processing,2011,10(3):297-305.

[10] WANG X W, XIA L X, WANG Z Y, et al. Hierarchical quantum-information splitting[J]. Optics Communications,2009,283(6):1196-1199.

[11] WANG X W, ZHANG D Y, TANG S Q. Hierarchical quantum information splitting with six-photon cluster states[J]. Inter J Theor Phys,2010,49(11):2691-2697.

[12] WANG X W, ZHANG D Y, TANG S Q, et al. Multiparty hierarchical quantum-information splitting[J]. J Physics:Atomic Molecular Optical Physics,2011,B44(3):035505.

[13] BAI M Q, MO Z W. Hierarchical quantum information splitting with eight-qubit cluster states[J]. Quantum Information Processing,2013,12(2):1053-1064.

[14] 王作栋,徐玮,黄亦斌,等. 2粒子未知态的受控分级量子通信[J]. 江西师范大学学报(自然科学版),2014(4):374-377.

[15] PENG J Y, BAI M Q, MO Z W. Hierarchical and probabilistic quantum state sharing via a non-maximally entangled state[J]. Chinese Physics,2014,B23(1):010304.

[16] XU G, WANG C, YANG Y X. Hierarchical quantum information splitting of an arbitrary two-qubit state via the cluster state[J]. Quantum Information Processing,2014,13(1):43-57.

[17] NANDI K, PAUL G. Quantum information splitting using a pair of GHZ states[J]. Quantum Information and Computation,2015,15(11/12):1041-1047.