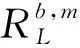广义Riesz变换高阶交换子的CBMO估计
钟海萍, 周伟松, 张京友, 王兴武
(1. 豫章师范学院 自然科学系, 江西 南昌 330103; 2. 重庆邮电大学 系统理论与应用研究中心, 重庆 400065; 3. 重庆三峡学院 数学与统计学院, 重庆 404000)
近年来,随着偏微分方程、算子理论、多复变函数理论、位势理论和几何分析等学科的不断发展,许多数学学者开始关注非光滑区域上的奇异积分或者非光滑核上的奇异积分理论,二阶复函数椭圆型散度算子L有关的Riesz变换是其中一个典型的例子.
定义一个二阶散度型椭圆算子Lf=-div(Af),A=A(x)是指一个定义在Rn上的复的、L系数的n×n矩阵,且满足一致性椭圆条件:存在0<λ≤γ<,使得
其中ξ、ζ∈Cn.
定义Littlewood-Paley-Stein型函数Gf(f)为
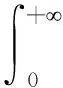
由此利用算子的谱理论,定义算子L的广义Riesz变换为
RL=
(1)
当L=-Δ,即Rn上的Laplacian算子,以上广义Riesz变换是通常意义的Riesz变换.
设Kt(x,y)是t1/2e-tL的核,相应的与CBMO函数b(x)生成的高阶交换子
定义
(2)
设pt(x,y)是解析半群e-tL的热核,若满足A是实矩阵,或A是n≤2的复矩阵,或者当n≥3时核是Hölder连续的[1],那么pt(x,y)具有Gaussian上界,即
(3)
由此,本文给出热核的2个假定[2-3].
(a) 设全纯半群为e-zL,|arg(z)|<π/2-θ核为az(x,y),对所有的v>θ,核az(x,y)满足Poisson上界.|arg(z)| |arg(z)|<π/2-v, (b) 算子L在L2(Rn)上满足有界H全纯演算.关于H全纯演算相关定义定理参见文献[1,4]. 定义1.1[9]设α∈R,0 其中 当p=时取通常意义的极限形式. 定义1.2[8]设1≤q<,称f∈CBMOq(Rn),如果有 ‖f‖CBMOq= 其中B(0,r)={x∈Rn:|x| 引理1.1[1]设n≥2,L满足(1)和(2)式,设Kt(x,y)是t1/2e-tL的核,则存在常数c>0使得 引理1.2[3]设L满足假定(a)和(b),那么是弱(1,1)型并且在Lq(Rn)上有界,其中1 引理1.3[8]设f∈CBMOq(Rn),1≤q<,r1,r2>0,t那么 1 证明只考虑0 则有 E1+E2+E2. (4) 对于E2,根据Minkowski和Hölder不等式,因此得到 mBk(b))|i‖Lq/i‖χk|(b(y)- mBk(b))|m-i‖Lq/(m-i)‖fj‖Lq1≤ (5) 根据引理1.2有 (6) 对于E1,当x∈Ak,y∈Aj,注意到j≤k-2,2k-2≤|x-y|≤2k+1,根据Minkowski和Hölder不等式 E11+E12. (7) 对于E11,由引理1.3得 (8) 令 因此得到 (9) 再应用引理1.1,有 (10) 因此 ‖fj‖Lq1(Rn)2-kα22jα1. (11) 对于E12,由引理1.3得 |(b(x)-mBj(b))|i× (12) 令 类似于(10)式的估计得 (13) 因此得 ‖fj‖Lq1(Rn)2-kα22jα1. (14) 结合E11和E12的估计,得 令 (15) (16) 对于E3,注意到k≤j-2,当x∈Ak,y∈Aj,有2j-2≤|x-y|≤2j+1.类似E1的估计过程,得到 (17) (18) 定理2.1的证明完毕. 设E,F为Rn上的闭子集,dist(E,F)表示集合E与F的欧氏距离,f是n-tupple函数.关于L2off-diagonal估计的引理如下. 引理3.1[5]设E和F是Rn上的闭子集,那么对于所有的t>0,有 ‖f‖Lp(E),suppf⊂E; ‖f‖Lp(E),suppf⊂E; ‖f‖Lp(E), suppf⊂E; ‖f‖Lp(E),suppf⊂E, 定理3.1设RL如(2)式所定义, λ≥0, 1 α2满足 则有 Q1+Q2+Q3. (19) 对于Q2,根据引理3.2以及Hölder不等式,类似E2的估计得到 (20) 对于Q1,注意到 x∈Ak, j≤k-2, y∈Aj, 2k-2≤|x-y|≤2k+1, 由Minkowski和Hölder不等式,得 ‖L-1/2(fj)χk‖Lq2(Rn)≤ (21) 根据引理3.1,得 ‖L-1/2(fj)χk‖Lq2(Rn)≤c2(kn/q2-kn/2)× (22) (23) 最后估计Q3,注意到当x∈Ak,y∈Aj,k≤j-2,有 2j-2≤|x-y|≤2j+1, 由引理1.3类似于Q1,得 ‖L-1/2(fj)χk‖Lq2(Rn)≤c2(k-j)(n/q1-n/2+α1)× 2-kα22jα1‖fj‖Lq1(Rn). 致谢重庆邮电大学博士启动基金(A2016-80)和重庆邮电大学大学生科研训练计划项目(A2017-71)对本文给予了资助,谨致谢意. [1] AUSCHER P, TCHAMITCHIAN P. Square Root Problem for Divergence Operators and Related Topics[M]. Paris:Societe Mathematique de France,1998. [2] HOFMANN S, MARTELL M J.Lpbounds for Riesz transforms and square roots associated to second order elliptic operator[J]. Pub Math,2003,47:497-515. [3] DUONG X T, MCINTOSH A. TheLpbonudedness of Riesz transform associated with divergence form operators operators[J]. Center for Math and Appl Australian National Univ,1999,37:15-25. [4] MCINTOSH A. Operators which haveHcalculus, Miniconference on operators theory and partial differential equations[J]. Proc Centre Math Anal Austral Nat Univ,1986,14:210-231. [5] AUSCHER P. On Necessary and Sufficient Conditions forLpEstimates of Riesz Transform Associated to Elliptic Operators onRnand Related Estimates[M]. Rhode Island:Mem Am Math Soc,2007. [6] FAN D S, LU S Z, YANG D C. Boundedness of operators in Morrey spaces on homogeneous its applications[J]. Acta Math Sinica,1999,14(14):625-634. [7] FAN D S, LU S Z, YANG D C. Regularity in Morrey spaces of strong solutions to nondivergence elliptic equations with VMO coefficients[J]. Georgian Math J,1998,5(5):425-440. [8] LU S Z, WU Q. CBMO estimates for commutators and multilinear singular integrals[J]. Math Nachr,2004,276(1):75-88. [9] LU S Z, XU L F. Boundedness of rough singular integral operators on homogeneous Morrey-Herz spaces[J]. Hokkaido Math J,2005,34(2):299-314. [10] LU S Z, TANG L, YANG D C. Boundedness of commutators on homogeneous Herz spaces[J]. Sci China,1998,A41(10):1023-1033. [11] 杨明华,许明,张学铭. 广义分数次积分算子在齐次Morrey-Herz空间上的有界性[J].暨南大学学报(自然科学与医学版),2012,33(3):239-243. [12] LU S Z, YANG D C, ZHOU Z S. Sublinear operators with rough kernel on generalized Morrey spaces[J]. Hokkaido Math J,1998,27(1):219-232. [13] 陶双平,杨沿奇. 变量核奇异积分与分数次微分的加权Morrey-Herz空间有界性[J]. 吉林大学学报(理学版),2016,54(4):667-684. [14] 李睿,陶双平. 多线性奇异积分算子在加权Morrey-Herz空间上的有界性[J]. 西南大学学报(自然科学版),2016,38(10):62-67. [15] WU J L. Boundedness of multilinear singular integral operators on the homogeneous Morrey-Herz spaces[J]. Ukrainian Mathematical J,2009,61(10):1684-1693.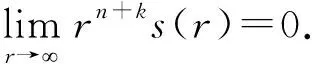
1 预备知识
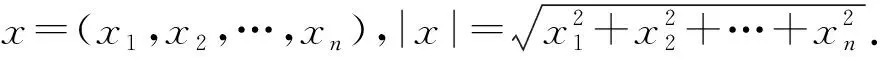
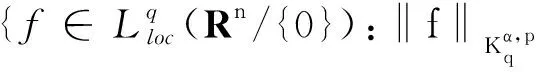
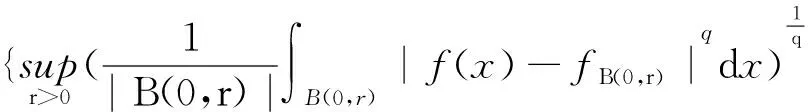
2 主要结果及其证明
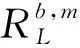
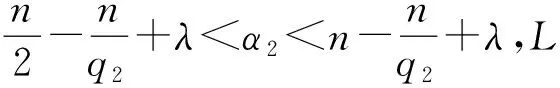
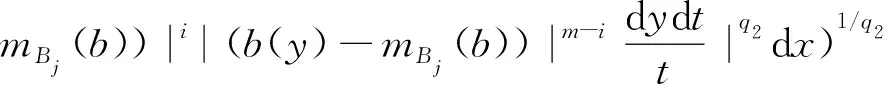

3 L2off-diagonal估计