元胞蚂蚁算法的参数优化方法及其仿真研究

王培良，张 婷，肖英杰

（1.上海海事大学 商船学院，航运仿真技术教育部工程研究中心，上海 201306；2.山东交通职业学院 航海学院，潍坊 261206；3.潍坊科技学院，潍坊 262700）

0 引言

上世纪90年代初，意大利学者M.DORIGO等人提出了具有正反馈机制和鲁棒性的蚂蚁算法，此后国内外学者充分利用并优化该算法解决诸如旅行商、路径规划等问题，均取得良好效果。同时蚁群算法（Ant ColonyOptimization，ACO）的参数选取与组合对算法性能的影响问题亦成为专家学者们的研究对象。

王旭[1]通过研究提出蚁群算法与Dijkstra算法相比，搜索近似最优路径的能力更强，时间更快，但地图离散化未能最优。胡启国[2]通过优化信息素更新和状态转移规则，解决了算法容易陷入局部最优解的问题，但其旨在优化最优冗余分配问题。尹宇洁[3]通过研究优化启发函数和禁忌表提出，基于蚁群优化算法的元胞自动机模型（Cellular Automata，CA）能够获得比基于经典CA模型更优的最佳疏散路径，但CA的邻域选择问题未能优化，同时也未能对时间标准进行统一[4]。冯韦韦[5]提出将ACO算法的信息素采用遗传算法的复制思想进行更新，结合单一的禁忌规则，可得到指定个体的最优疏散路径。李东妮[6]将蚁群算与遗传算法相结合，加入交叉、变异算子，增加了获得全局最优解的概率。总之，现有研究主要依据传统的ACO算法的更新规则等进行优化[7,8]，无法做到参数的自适应调整。

鉴于上述[9]，笔者将元胞蚂蚁算法与粒子群优化算法（Particle Swarm Optimization，PSO）相结合[10,11]，在同一时间坐标的基础上[12～15]，对算法参数进行优化设计[16～18]。最终通过仿真，验证该方法对解决路径规划问题的科学性与有效性。

1 元胞蚂蚁算法描述与构建

1.1 栅格地图的描述

传统ACO算法对旅行商、路径规划等问题进行仿真求解时，均使用四边形栅格地图背景，其邻域使用Moore型，如图1所示。

其中，灰色为中心元胞即蚂蚁当前所在位置，其邻域元胞可表示为N={s1，s2，…，si}，i∈[1，8]，si∈[0，1]，i和si均取整数，i表示邻域元胞编号，si表示邻域元胞是否被选中，取1时表示被选中。

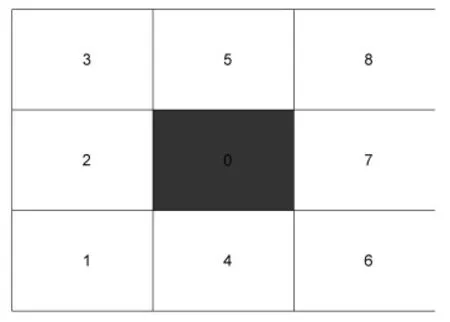
图1 moore型邻域

在使用四边形栅格地图进行仿真时，假设栅格的边长为e，如若当前蚂蚁下一步移动的位置选择极轴方向栅格，则其移动距离为e，但若选择斜向方向栅格，则移动距离为，如图2(a)所示。假设蚂蚁移动速度v不变，则蚂蚁每次移动时所需时间为e/v或者，导致求解时单步运行时间无法确定，时间标准无法统一，从而影响仿真的科学性。

为解决上述问题，笔者研究使用六边形栅格作为仿真地图背景。在栅格边长和蚂蚁移动速度均不变的情况下，则蚂蚁每次选择各方向的移动距离均为，如图2(b)所示，每次移动的时间步长是确定、统一的。同时六边形栅格能够有效避免出现与实际情况不符合的“斜向穿墙”现象。栅格地图中黑色元胞表示障碍物或者边界。

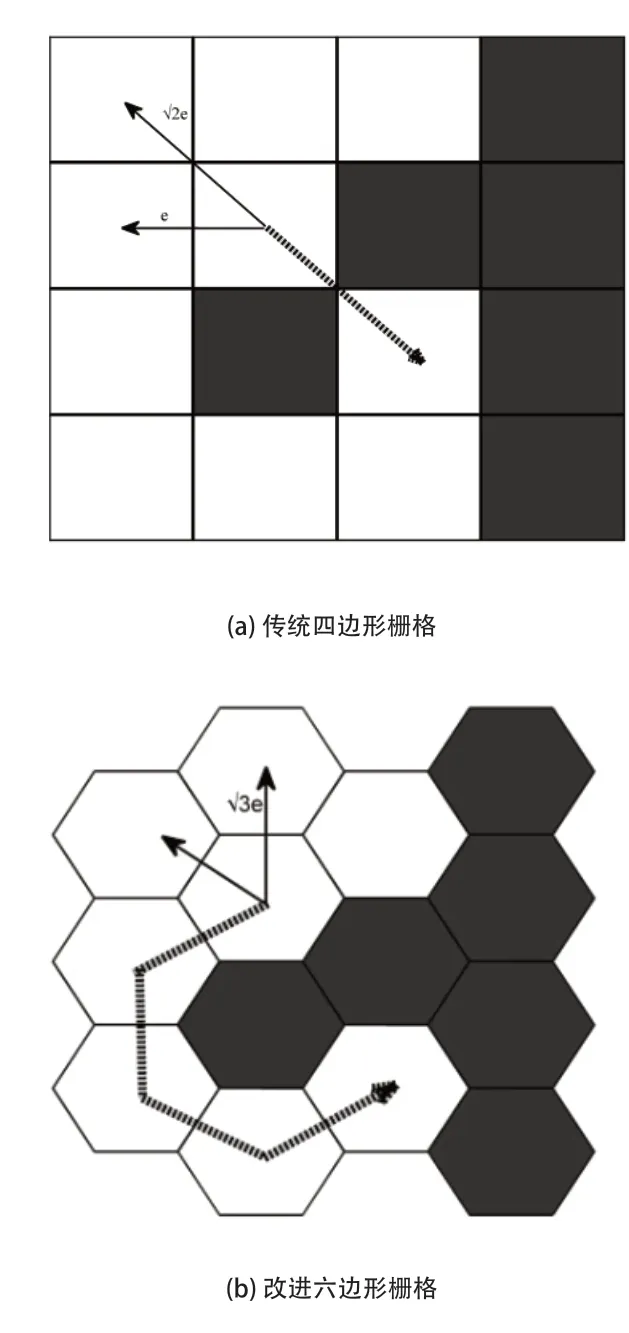
图2 四边形栅格与六边形栅格对比

因此，以竖直方向为Y轴、原点在左下角的笛卡尔坐标系建立仿真地图，同时设每个栅格的内切圆心为中心坐标点，则仿真地图网格坐标点（xi，yi）与网格序号i可通过公式进行转换：

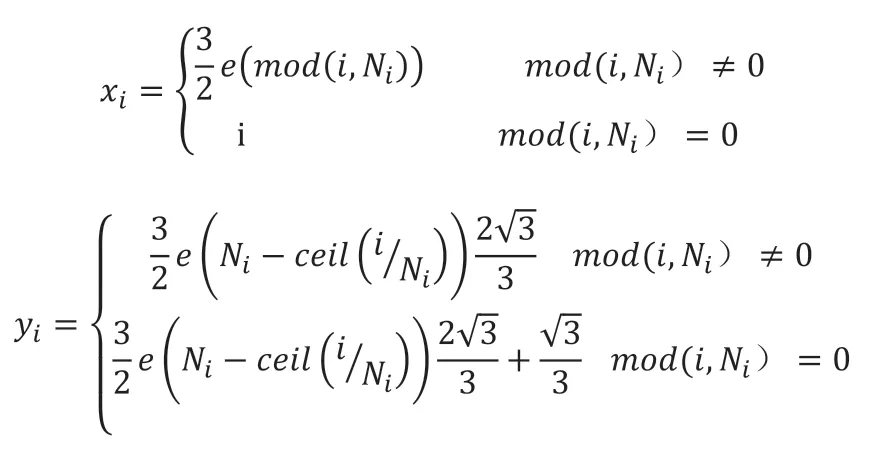
其中，Ni为地图尺寸即每行包含栅格的个数，ceil为朝正无穷大方向取整函数，mod为取模（取余）运算函数。

1.2 算法描述

元胞蚂蚁算法表达式为A=（Gm×n，Qm×n，S，Cw，N，R），其中：

A：单蚁元胞模型；

Gm×n：栅格地图信息矩阵；

Qm×n：信息素矩阵；

m和n表示矩阵的行列数，m一般与单次迭代蚂蚁数量相同；

S：元胞状态，其值为{0，1}，1表示此元胞被占用；

Cw：C为元胞空间，w表示空间维数，C要从G中获取，故w取2维；

N：元胞邻域；

R：元胞规则，即蚂蚁移动的基本依据，其规则主要取决于以下三点：

1）所选元胞不能为障碍物或边界；

2）所选元胞与目的元胞的距离应不大于当前元胞与目的元胞的距离；

3）各备选元胞被选中的概率由信息素计算公式决定，如下式：

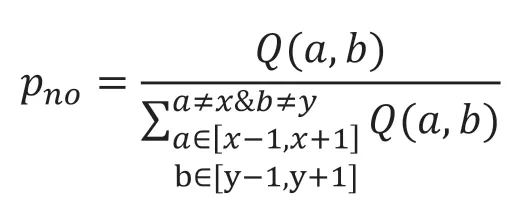
其中，（x，y）为某时刻中心元胞在元胞空间中的坐标,a和b表示矩阵的行号、列号，no表示可选元胞编号。

2 基于PSO的参数优化设计

2.1 PSO算法描述

PSO算法是上世纪90年代，学者Eberhart与Kennedy借鉴鸟类的觅食行为，提出一种基于种群的全局随机优化算法。该算法中的每个粒子都为目标问题的可行解，其粒子质量优劣适应度函数评价。每个粒子根据自身及其他粒子的位置信息不断调整移动速度，同时调整移动的方向和距离，从而实现粒子在解空间内的全局寻优。在算法求解的迭代过程中，粒子通过个体极值和全局极值调整自身的速度与位置，其公式如下：

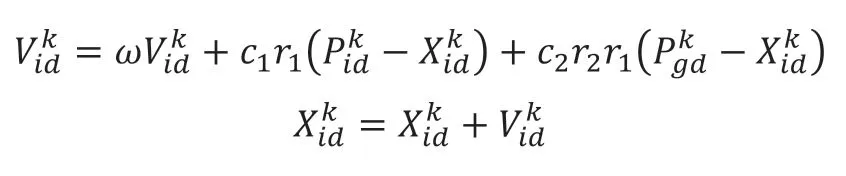
其中，V表示粒子速度；X=（X1，X2，X3，… Xn）为D维空间n个粒子组成的种群，分别代表粒子当前位置；ω为惯性权重；d=1，2，…，D；i=1，2，…，n表示粒子编号；k为当前迭代次数；Pid为个体极值；Pgd为全局极值；c1和c2为非负常数，称为加速度因子；r1和r2为介于[0，1]之间的随机数。

同时为了有效克服PSO算法存在的易早熟收敛、后期迭代效率低等缺点，本文节点遗传算法中的变异思想，在传统PSO算法中引入变异操作，即以一定的概率值对重新初始化某些粒子，从而产生自适应变异粒子。

2.2 适应度评价函数设计

在PSO算法进行参数优化过程中，适应度函数作为评价所选粒子即元胞蚂蚁算法参数的标准，因此，适应度函数的设计至关重要。综合考虑元胞蚂蚁算法在求解路径规划时的寻优能力、运行时间、收敛速度、稳定性等影响因素，笔者设计的适应度函数如下：

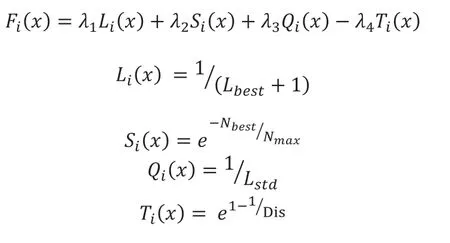
其中，Fi（x）为第i个粒子代表的参数所对应的适应度函数值；λ1、λ2、λ3、λ4为权重系数，且满足λ1+λ2+λ3+λ4=1；Li（x）表示使用粒子i运算所得的参数，元胞蚂蚁算法搜索最优路径的能力；Lbest表示每次PSO迭代所得到的最优路径的元胞数量；Si（x）表示使用粒子i运算所得的参数，元胞蚂蚁算法收的敛速度；Nbest为元胞蚂蚁算法搜索到当前最优路径时自身的迭代次数；Nmax为元胞蚂蚁的最大迭代次数；Qi（x）表示使用粒子i运算所得的参数，元胞蚂蚁算法的稳定性；Lstd为每次PSO迭代过程中，元胞蚂蚁算法搜索到的路径的方差；Ti（x）表示使用粒子i运算所得的参数，元胞蚂蚁算法的运行时间；Dis表示元每次PSO迭代过程中，元胞蚂蚁算法搜索路径总和。

2.3 参数优化设计流程

元胞蚂蚁算法参数优化方法的思想是将参数作为PSO算法的位置信息进行迭代优化求解，将迭代得到的位置信息结果作为元胞蚂蚁算法求解路径规划问题的一个解，并利用适应度函数对解的性能做出评价，从而引导PSO算法的粒子趋向于适应度值更高位置。其算法步骤如图3所示。

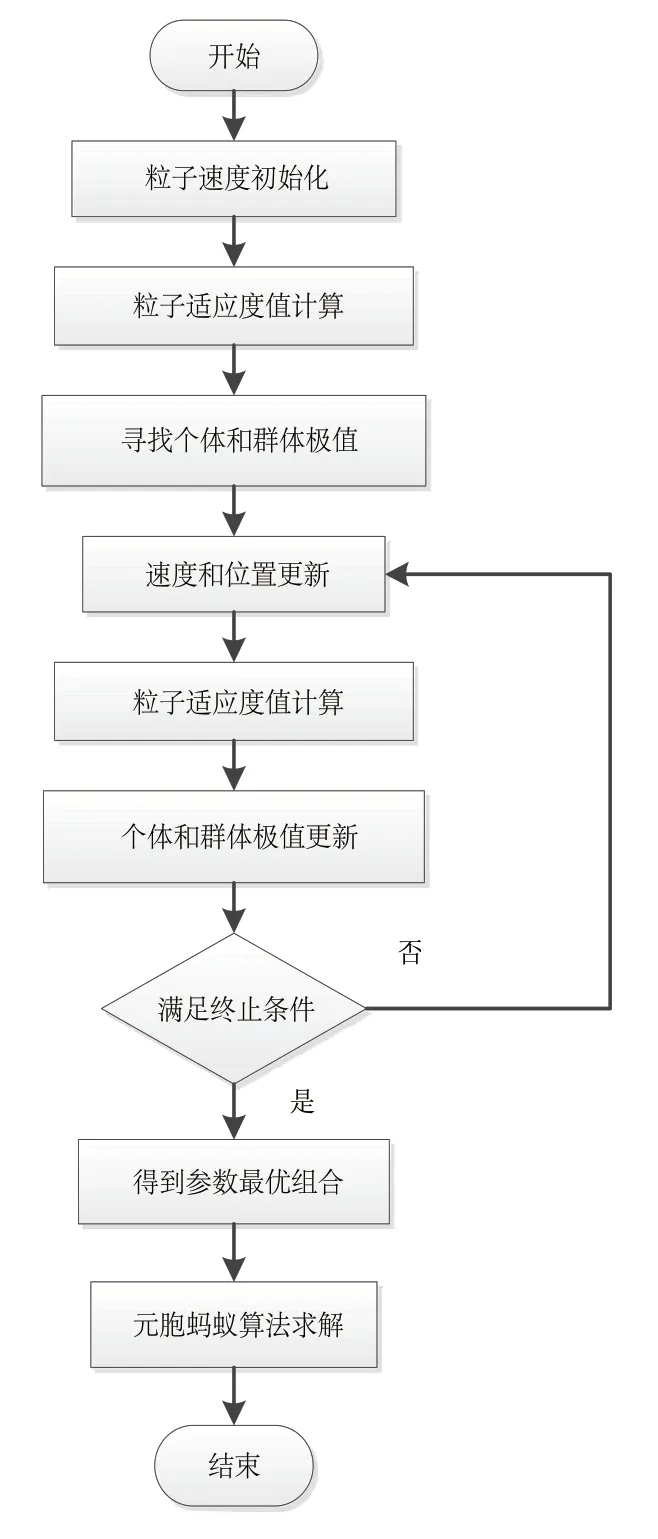
图3 算法流程图

3 仿真结果及分析

为验证所构建模型的性能，笔者以某大型邮轮的B甲板上的展厅为工程背景进行仿真，计算对比蚁群元胞算法与传统算法的优劣，邮轮B甲板构造详情如图4所示。

甲板中间位置展厅面积为20m×20m的封闭空间，其构造详情如图5(a)所示，仿真环境为20×20的栅格地图，如图5(b)所示。

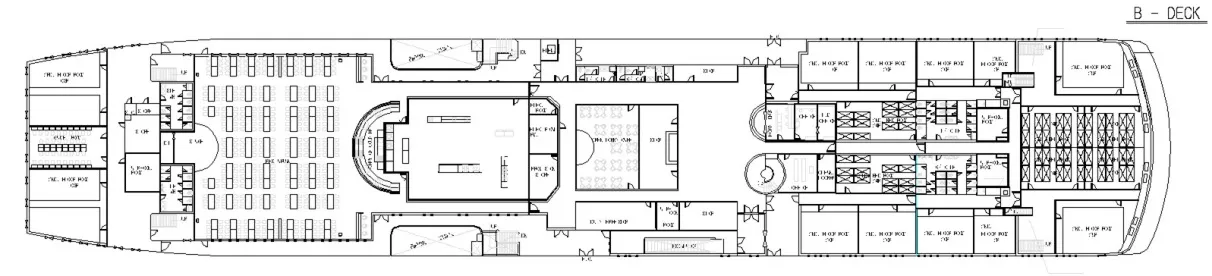
图4 某邮轮B甲板构造图

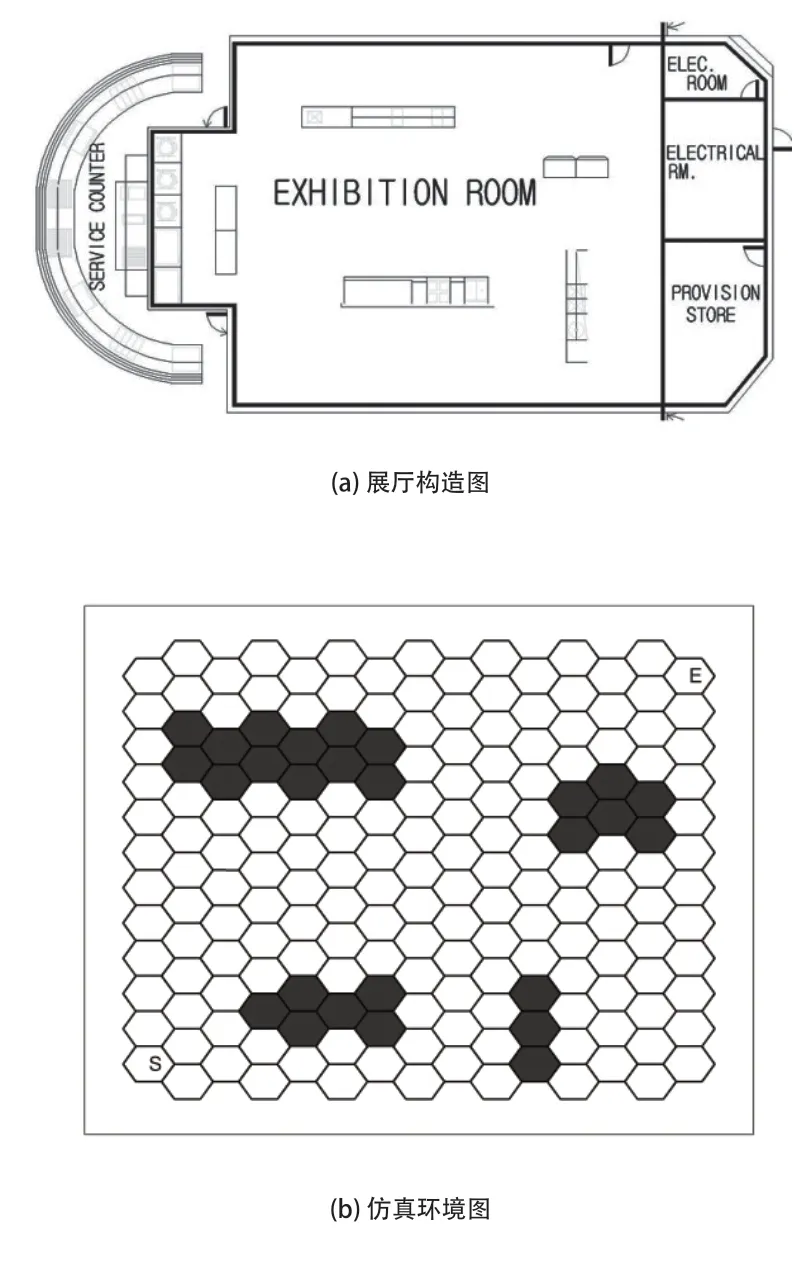
图5 展厅构造与仿真图

3.1 参数优化仿真

将元胞蚂蚁算法的参数作为PSO算法的优化对象，其中包括信息素启发因子α、期望启发因子β、信息素挥发因子ρ，其取值范围如表1所示，其余参数根据专家经验法进行设置，蚂蚁个数设置为30，信息素强度为14。具有自适应变异粒子的PSO算法的参数取值分别为：

c1=c2=1.49445；ω=0.5×（Tmax-t）/Tmax+0.2，Tmax=50为算法最大迭代次数，t为当前迭代次数；粒子个数为20；λ1、λ2、λ3、λ4分别为0.7、0.1、0.1、0.1。

根据仿真环境分别进行两次运算，所得结果如表2所示。

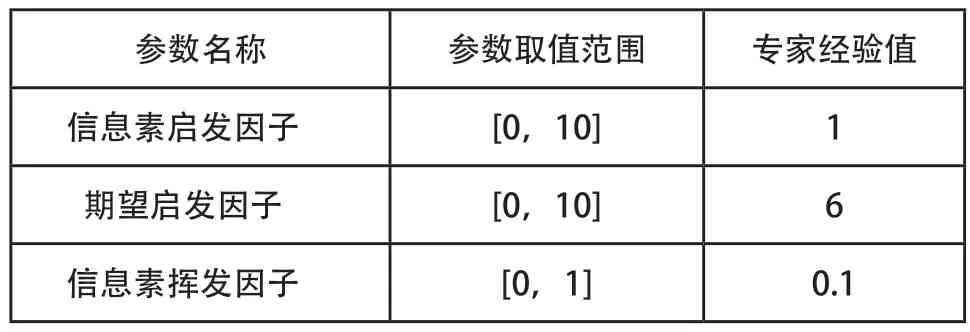
表1 元胞蚂蚁算法参数取值范围

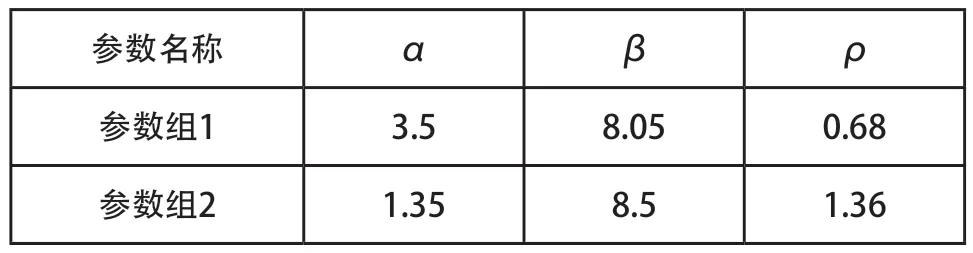
表2 仿真运算结果

为形象展现两组参数所对应粒子的适应度值的变化趋势与过程，绘制适应度值曲线如图6所示：

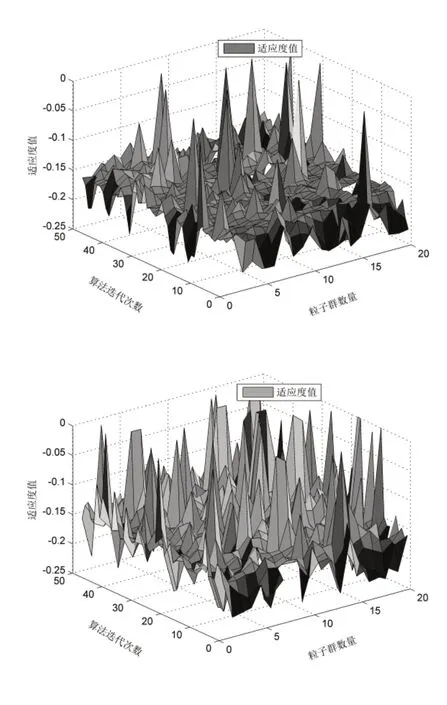
图6 粒子适应度值曲线

由图6可知，在PSO算法迭代过程中，两组粒子的适应度值存在一定的随机波动，但是从整个运行过程分析，其适应度值均表现出上升趋势，因此说明通过不断的迭代过程，粒子趋向于适应度值更优的位置。

3.2 路径规划结果

为四边形栅格地图与六边形栅格地图的有效性，分别对仿真环境进行路径规划，其结果如下：

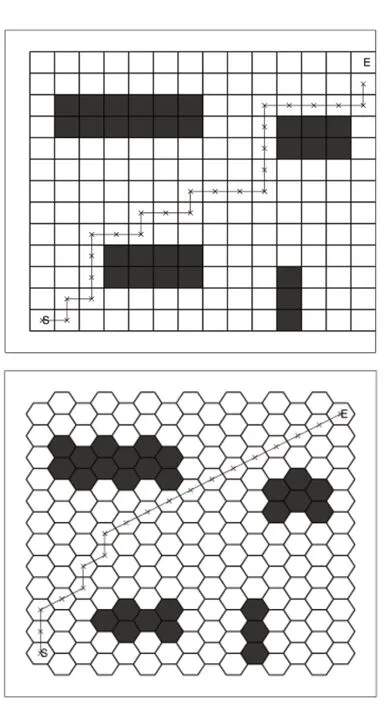
图7 仿真效果图

图中S表示起始节点，E表示目的节点。从上图中可知，传统模型与元胞蚂蚁算法均可进行有效路径规划。

3.3 路径规划性能分析

为进一步凸显本文研究方法的优势，分别使用基于四边形栅格地图的传统ACO算法、基于经验参数值的元胞蚂蚁算法以及基于PSO算法的元胞蚂蚁算法（两组参数结果）进行仿真对比，使用算法在进行路径搜索时所经过的元胞总数进行对比分析，其结果如图8所示。

由图8(a)与图8(b)对比分析可知，在搜索路径时，传统ACO算法与元胞蚂蚁算法所经过的元胞总数随着迭代次数的增加而逐渐减少；在算法迭代次数相同的情况下，元胞蚂蚁算法经过的元胞总数明显小于传统算法，表明元胞蚂蚁算法的搜索速度较快；随着迭代的不断进行，传统算法的搜索已基本停滞，而元胞蚂蚁算法仍在进行，表明元胞蚂蚁算法的搜索能力较强。对比分析图8(b)、图8(c)、图8(d)可知，基于经验值的元胞蚂蚁算法的收敛速度和搜索速度明显弱于参数组1、2，但是收敛性比参数组1强，参数组2 在收敛速度、搜索能力以及收敛性方面均表现出明显优势。

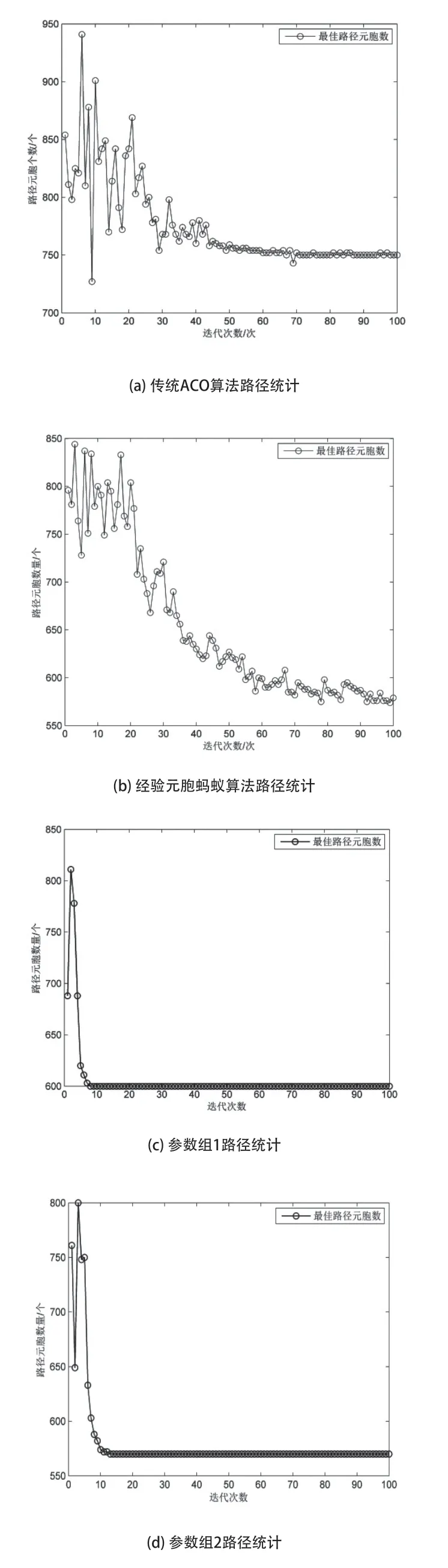
图8 算法性能对比图

4 结语

为求解路径规划问题，在传统ACO算法基础上，本文以六边形栅格为基础的元胞蚂蚁算法，提出了基于PSO算法对元胞蚂蚁算法的参数进行优化的策略。将元胞蚂蚁算法的参数作为PSO算法的位置信息进行迭代求解，利用适应度函数值对求解性能做出评价，从而得到元胞蚂蚁算法的最优参数组合。仿真结果表明；该方法能够有效实现对元胞蚂蚁算法的参数选取，对元胞蚂蚁算法应用于路径规划具有一定的实用意义。