盾构穿越邻近桥梁桩基的影响因素分析
李世仲
(中铁建设集团有限公司 北京 100040)
1 引言
随着城市地铁建设和地下空间开发的快速发展,新建隧道穿越邻近桥桩、地下室及其它地下建构筑物的情况越来越多。 地铁盾构隧道施工对邻近桥桩的影响主要表现在盾构施工引起邻近土体的扰动,从而引起桥桩的沉降、侧移和桩体的受力和弯矩等,进而影响桩侧摩阻力与桩基承载力。 同时,由于桥梁桩基的阻隔效应,盾构施工引起的地表沉降也与无受限条件情况存在差别。 在对隧道近接桥桩的分析研究中,主要采用的有数值计算法、模型实验法以及数值计算和实验对比分析的研究方法。
Loganathan 等[1]通过提出边界元对盾构隧道施工开挖过程中近接桥梁桩基的单桩和群桩进行分析研究,并假设桩基和地层都是各向同性,桩土之间不发生相对滑移。 Mroueh 等[2]采用三维有限元数值模型模拟隧道近接桥桩施工,分析桥桩产生的轴力和弯矩,结果表明内力的分布情况主要由桩顶和隧道轴线的相对位置和桥桩轴线与隧道开挖面中心线的距离共同决定。 Lee 等[3]通过三维有限元模型分析了隧道近接单桩时,隧道开挖过程对桩体内力的影响,并采用离心模拟试验来对比分析数值计算结果,验证了模型试验和数值计算的准确性。况龙川等[4]针对不同桩基施工与隧道之间的最小安全距离,结合现场监测数据,对隧道邻近的地下连续墙、钻孔灌注桩等开挖产生的隧道位移影响进行分析,总结了不同施工方式对于隧道的影响。郑骐[5]研究分析穿越部分地层在二次扰动情况下,其地表沉降的变化规律和控制措施。 徐前卫等[6]对盾构隧道穿越桥梁桩基中部为基础进行数值模拟并引入了对除桩技术的探讨。 宋欣等[7]采用MIDAS有限元软件建立三维数值模型,主要分析盾构隧道在开挖过程中对桩基的影响,总结了对于盾构隧道邻接桥桩施工时的保护控制措施。 徐慧宇等[8]对下穿高速桥区间隧道进行设计,分析区间隧道施工过程中对地表变形影响,总结了盾构施工影响地层变形的规律。 沈建文等[9]通过对盾构隧道和桥梁相互位置的建模分析,并与监测结果进行对比,论证了数值模型的准确性。 单生彪等[10]运用MIDAS/GTS 有限元软件对盾构隧道近接群桩穿越进行动态模拟,计算出衬砌管片中的变形和内力进行对比分析。 郭波[11]通过建立结构-桥墩-土体有限元模型,分析了盾构施工过程中高铁桥墩的变形特征,对工程安全性进行评估。 游辉[12]通过建立盾构下穿地桥的三维有限元模型,分析了不同模拟施工步下桥桩竖向及水平位移变化规律和承台竖向位移及差异沉降结果,分析表明:在盾构施工控制措施外,需要辅助以洞外隔离保护措施,保证结构处于安全状态。
本文利用三维数值模拟的方法,对杭州市庆春路过江隧道的实际情况进行简化,并加入桥梁桩基等构筑物,建立了盾构隧道-桥梁桩基数值模型,对不同隧道埋深、桩间距、桩基埋深和隧道穿越部分土体弹性模量进行模拟计算,并进行对比分析新建隧道对地表沉降的影响和对既有桥桩的受力和变形影响,对工程实践具有一定的指导意义。
2 试验方法与模型简介
2.1 正交试验介绍
在研究盾构穿越邻近桥梁桩基的影响因素分析时,需要考虑很多影响因素,其中盾构隧道埋深、桥梁桩基的桩间距(假定隧道从两桩间距中点处穿越)、桩基埋深、隧道穿越土体弹性模量等因素在盾构隧道穿越桥梁桩基时施工扰动方面起着重要作用。 用正交分析法来分析计算上述四个因素在盾构隧道穿越桥梁桩基时引起的地表位移和桩基位移及受力,并计算地表横向沉降变形的权重。
在进行正交方法计算之前,为了消除变量的量纲效应,先将各参数与隧道直径d 和土体重度γ 进行无量纲化处理,在进行无量化处理之前,假定隧道垂直穿越两桥桩间距中点位置;隧道管片外径10.0 m,内径9.0 m,厚0.5 m,环宽2.0 m;隧道穿越部分,土体重度为20(kN/m2)。 将需要分析的参数,在合理范围内取值,隧道埋深H =10 m,15 m,20 m,则H/d =1,1.5,2;桩基间距D =15 m,25 m,40 m,则D/d =1.5,2.5,4;桩基深度L =15 m,20 m,30 m,则L/d =1.5,2,3;隧道穿越土体弹性模量E =10 MPa,20 MPa,30 MPa,则E/γd=5,10,15。 对四因素三水平叠交影响因素的试验进行安排,叠交影响因素试验如表1 所示。

表1 叠交影响因素试验
将三维有限元计算结果代入正交试验方法中,通过变化研究因素中的某一个因素进而得到不同的工况模型和计算结果,并与其余工况计算结果进行对比综合分析。
2.2 计算模型和参数选取
结合隧洞开挖过程中,隧道埋深、掘进压力、盾尾注浆和应力释放系数因素,对杭州市庆春路过江隧道模型进行简化,再加入桥桩进行分析讨论,简化后模型尺寸为100 m(X) ×60 m(Y) ×60 m(Z),隧道管片外径d 为10.0 m,内径9.0 m,厚0.5 m,环宽2.0 m,桥台尺寸为6 m(X) ×6 m(Y) ×2 m(Z),桥梁桩基位于矩形桥台中心处,桥台上部荷载取20 kPa,模型简图如图1 所示,参数选取表如表2所示。

表2 地层和材料参数选取

图1 有限元模型
3 各影响因素分析
3.1 地表纵向位移
隧道近接桥桩施工过程中产生的地表纵向位移如图2 所示。 从图2 可以看出新建隧道在近接桥桩施工时,隧道埋深、桩基间距、桩基埋深和隧道穿越土体的弹性模量均会对施工中产生的地表纵向位移产生较为明显的影响。 对比分析可得,随着隧道埋深的加深,隧道在纵向的沉降总体呈现减小的趋势,且当隧道穿越部分土体弹性模量较小时,地面沉降较大,而桩基间距和桩基埋深的变化对于地表纵向位移影响程度相对较小,对图中纵向位移曲线无明显影响规律。

图2 地面纵向位移曲线
3.2 地表横向位移
隧道近接桥桩施工过程中产生的地表横向位移,即沉降槽曲线如图3 所示。
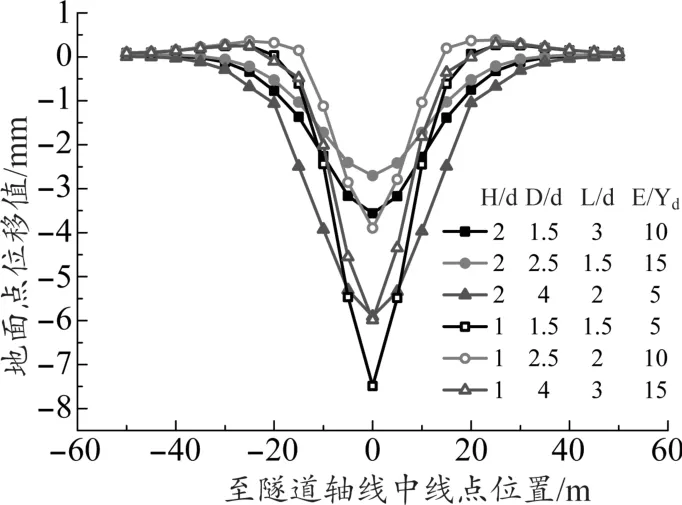
图3 地面横向位移曲线
通过图3 可以看出,当隧道埋深15 m,桩间距为25 m,桩基埋深为30 m,隧道穿越处土体弹性模量为10 MPa 时,地表横向沉降槽达到最大深度10.06 mm;而当隧道埋深20 m,桩间距为25 m,桩基埋深为15 m,隧道穿越处土体弹性模量为30 MPa时,地表横向沉降槽达到最小深度2.70 mm。 由此可以得出,隧道埋深越深,沉降槽宽度越大,地面最大沉降越小,曲线越平缓、稳定。
3.3 桩体竖向位移
隧道近接桥桩施工过程中产生的桩体竖向位移如图4 所示。
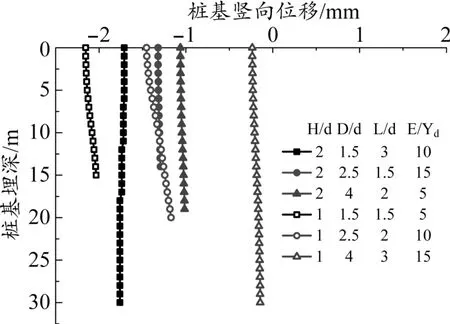
图4 桩体竖向位移
通过图4 可以看出,桩体竖向位移沿着桩身整体方向的沉降规律基本相同,桩体产生竖向位移的原因主要是由于新建隧道开挖过程中对桩体周围的土体产生了扰动,导致了土体的应力重分布,桥梁桩体和附近的土体之间产生相互作用力,从而在桩侧土体和桩顶荷载的共同作用下,桩体随之发生竖向位移。
3.4 桩体水平位移
隧道近接桥桩施工过程中产生的桩体水平位移如图5 所示。 通过图5 可以看出,桩体横向位移的变化规律基本相同。 桩基上部产生向隧道开挖侧位移的趋势,随着桥桩埋深的增加,桩基的水平位移逐渐向远离隧道开挖侧增大,根据图5 可以看出在隧道埋深附近横向位移曲线发生突变,位移量达到最大值,而后埋深再增加,横向位移增加量减小。
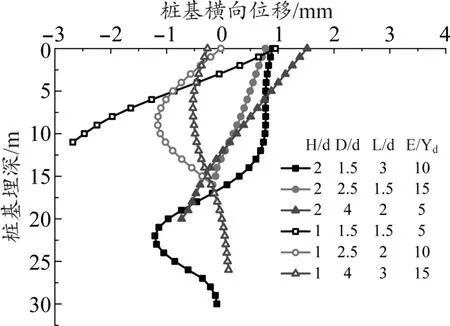
图5 桩体横向位移
3.5 桩体弯矩
隧道近接桥桩施工过程中产生的桩体弯矩如图6 所示。
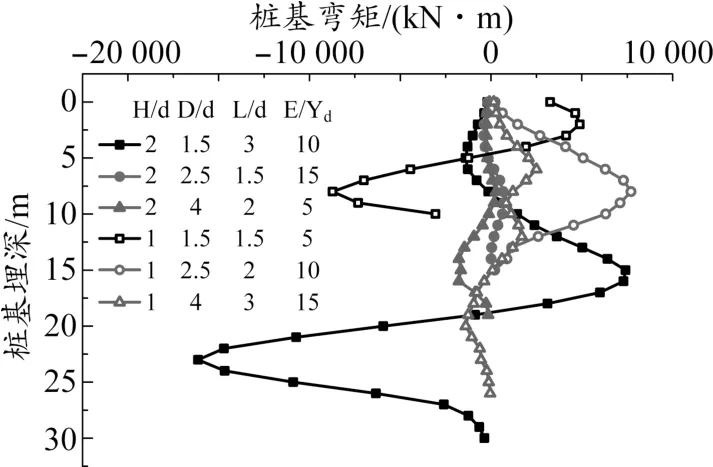
图6 桩体弯矩
通过图6 可以看出,桩体弯矩的变形规律基本相同,弯矩曲线随着桩基的埋深弯矩逐渐增大,在隧道埋深的上部3 ~4 m 处达到最大正弯矩,隧道埋深下部3 ~4 m 处达到最大负弯矩,在桩体两端弯矩值趋近于零。 对比图6,弯矩值随着隧道埋深的增加,弯矩增大;在穿越部分土体弹性模量较小的情况,弯矩曲线变形较为明显,反之,在桩间距较大,桩基埋深较浅时,弯矩曲线变形较为平缓。
4 正交试验结果分析
以地表横向位移变化曲线为例,探讨正交试验中的四个因素对盾构近接桥桩施工时地层体积损失率η 影响。 对盾构隧道近接桥桩施工时的地表横向沉降数据进行拟合,计算出在不同组合下的地层体积损失率η,并在此基础上,计算出的各因素的极差值Rj,通过对比极差值Rj推断出不同因素的主次关系。
将通过极差分析法与方差分析法处理的试验数据统计如表3 所示。
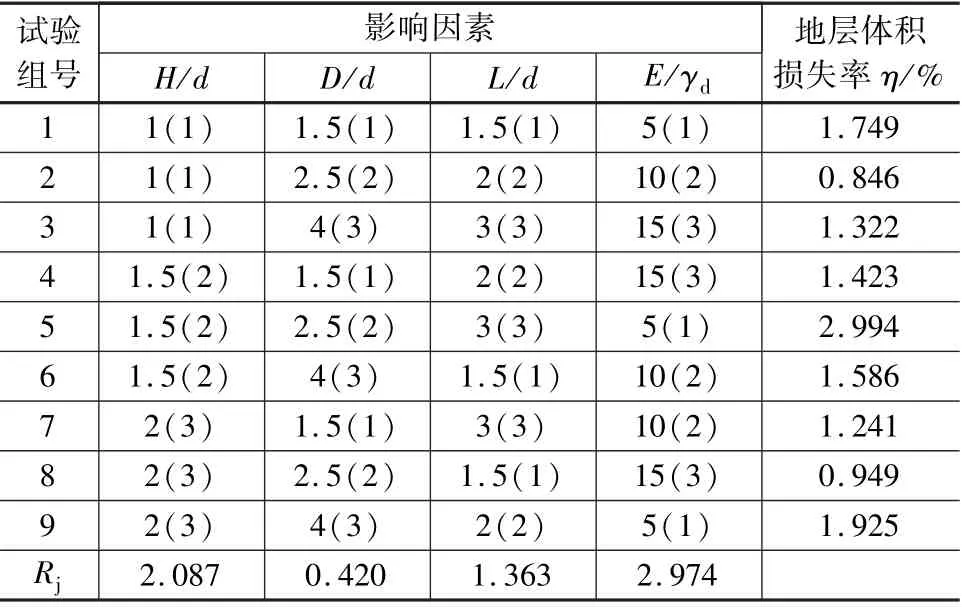
表3 正交试验分析结果
通过计算得出的极差值Rj,可以较为直观地看出不同因素对地层体积损失率η 影响的主次顺序,可以判断出对地层体积损失率η 的影响程度:穿越部分土体弹性模量与土体重度和隧道直径的比值E/γd>隧道埋深与隧道直径的比值H/d >桩基埋深与隧道直径的比值L/d >桩间距与隧道直径的比值D/d。
5 结论
本文利用正交试验方法,主要通过对隧道埋深、桩间距、桩基埋深和隧道穿越部分土体弹性模量参数进行研究,对地表的纵向和横向位移,桩体的竖向位移和水平位移以及桩体所受弯矩进行分析总结,并以地表横向位移变化曲线为例,对几个影响因素进行显著性分析,得出以下结论:
(1)由于新建隧道开挖过程中对桩体周围的土体产生了扰动,导致了土体的应力重分布,使得桩体周围土体向隧道开挖处发生收敛,进而在桥桩和其周围土体的相互作用下使得桩体产生变形和受力。
(2)地表纵向位移和横向位移规律基本一致,横向位移基本符合沉降槽曲线,随着隧道埋深越深,隧道穿越部分土体弹性模量的越大,沉降槽宽度越大,地面最大沉降越小,曲线越平缓、稳定。 桩间距和桩基埋深对于地表位移有一定影响,但是影响不太明显。
(3)在不同因素的影响下,桩体竖向位移变化规律相近,当隧道穿越部分土体弹性模量增大时,桩体竖向位移增加比较显著。 另外,当桩间距减小时,竖向位移会增大;而隧道埋深增加和桩基埋深的增加对于竖向位移增加影响较小。
(4)正交试验中的四个因素对地层体积损失率η 影响显著性为穿越部分土体弹性模量与土体重度和隧道直径的比值E/γd>隧道埋深与隧道直径的比值H/d >桩基埋深与隧道直径的比值L/d >桩间距与隧道直径的比值D/d。

