三平移机构设计与运动学符号解及性能评价
沈惠平 吉 昊 许正骁 杨廷力
(常州大学现代机构学研究中心, 常州 213016)
0 引言
三平移(3T)并联机构具有少自由度机构独有的结构紧凑、控制容易、造价低等优点,具有良好的工程应用前景[1-4]。
目前,已有许多国内外学者对其展开了研究。1988年,ClAVEL[5]设计了著名的Delta 机构,此后,一些学者提出了相应的类Delta[6-8]机构;KONG等[9]设计了一种新型的3-CRR机构,其特点在于不存在明显的奇异位置;李仕华等[10]设计了一种3-RRUR型3平移机构;杨廷力等[11-12]基于POC理论设计了多种新型3T机构,并分析了它们的拓扑特性;ZENG等[13]设计了一种三平移Tri-pyramid并联机构,分析了该机构的工作空间等特性;MAHMOOD等[14]设计了一种3-[P2(US)]的3T机构,分析了该机构的灵巧度等特性;李坤全等[15]以3-RPRP并联机构为原型,设计了一种全柔性并联机构;毛鹏飞[16]研究了不同分支的三平移并联机构;杜康等[17]研究了基于POC方程的三平移并联机构拓扑结构设计方法;贾明星[18]研究了3-RRC机构的运动和力传递性能,并分析了不同的支链布置方法及驱动关节对传递性能的影响;韩帅帅[19]以3-CPR机构为模板,提出了5种新机构,并对其进行分析;朱伟等[20]设计了一种弱耦合2RRP_aR+PP_aP三平移操作机器人机构,并分析其主要拓扑特征;叶海燕等[21]提出了空间曲线三平移机构的型综合及分类方法;孙驰宇等[22]对(RPa‖3R)2R+RPa型三平移机构进行刚度建模及分析。
文献[23]设计了一种新型3T机构,与上述大多数三平移机构类似,该机构并不具有正向位置符号解,这使得该机构的误差分析、动力学分析和尺度综合较为复杂。一般地,机构位置正解的形式有解析解、数值解,而解析解包括封闭解、符号解。其中,位置符号解对运动学和动力学性能分析最方便,因为可以用输入量表示全局奇异位形方程,进而进行操作度的性能评估及结构参数的全域优化;较易建立运动学误差模型,并进行影响因素的敏感度分析;计算工作空间方便、高效、准确;动力学建模方便、高效。然而,目前具有正向位置符号解的并联机构还较少。
本文根据基于方位特征方程(Position and orientation characteristics, POC)的并联机构拓扑结构设计理论和方法,设计一种具有正向位置符号解的新型三平移(3T)并联机构。分析该机构的POC集、自由度及耦合度(κ=0)等拓扑特征,对其进行运动学位置建模与分析,求得该机构位置正解符号表达式,基于逆解表达式推导该机构的工作空间;根据并联机构运动/力传递性能指标[24]对该机构进行运动/力性能分析,即基于螺旋理论求得各支链传递力旋量与约束力旋量,求得该机构各支链的输入传递指标、输出传递指标与局部传递指标表达式,得到两种指标曲线分布图;根据约束力旋量与输入、输出运动旋量的互易积,以及传递力旋量与输入、输出运动旋量的互易积等分析机构的奇异位型;最后,根据局部传递指标曲线评价机构距离奇异位型的远近。
1 机构拓扑设计及分析
1.1 机构设计
本文设计的具有正向位置符号解的3T并联机构如图1所示,定平台0(导轨)与动平台1之间通过两条混合支链Ⅰ、Ⅱ连接。
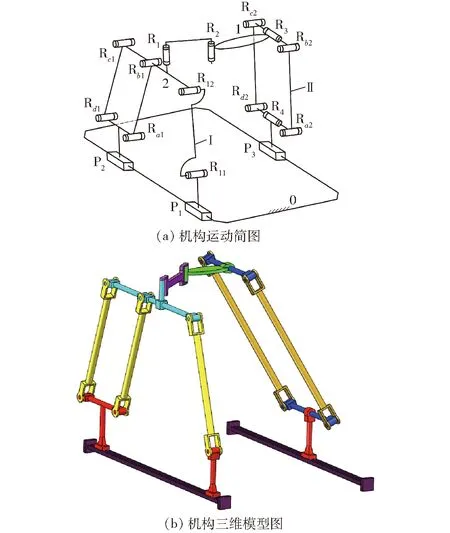
图1 具有正向位置符号解的3T并联机构Fig.1 3T parallel mechanism with forward position symbol solution
混合支链Ⅰ由移动副P1、P2,平行四边形副Pa1,转动副R11、R12、R1及R2组合而成。其中,移动副P1与定平台上的一侧导轨相连,然后,与轴线平行的转动副R11、R12依次串联,组成子链SOC1;移动副P2与移动副P1安装于同一导轨上,平行四边形副Pa1与之串联,组成子链SOC2,再将2条子链SOC1和SOC2,以R12、Rb1、Rc1共线的方式组成一个子并联机构(Sub-PM),而Sub-PM中所有转动副轴线平行于定平台0所在平面;最后,将2个轴线平行且垂直于定平台0平面的转动副R1、R2与Sub-PM串联组成混合支链Ⅰ,且混合支链Ⅰ通过转动副R2与动平台相连。
混合支链Ⅱ由移动副P3、平行四边形副Pa2、转动副R3、R4组成,其中,移动副P3与定平台上的另一侧导轨相连;然后,再与平行四边形副Pa2串联,转动副R3、R4分别位于平行四边形副两条短边的中点,支链Ⅱ通过转动副R3与动平台1相连接。
1.2 并联机构拓扑分析
1.2.1POC计算
机构的POC方程计算公式[11]为
(1)
(2)
式中MJi——第i个运动副的POC集
Mbi——第i条支链末端的POC集
MPa——机构动平台的POC集
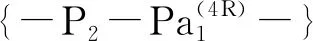
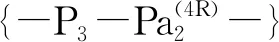
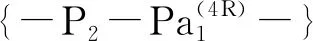
因此,子并联机构输出构件(p点)的运动为YOZ平面内的两维平动。
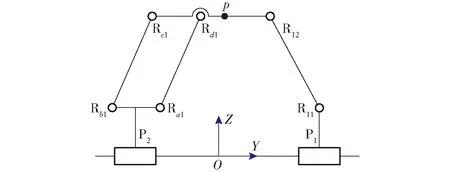
图2 HSOC1中的子并联机构Fig.2 Sub parallel mechanism in HSOC1
由式(1)求得第Ⅰ条HSOC1的POC集为
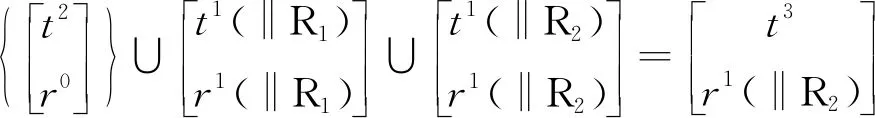
同理,由式(1)求得第Ⅱ条HSOC2的POC集为
于是,由式(2)求得机构的POC集为
因此,动平台1具有三维平移的输出特性。
1.2.2自由度计算
并联机构的全周DOF计算式[11]为
(3)
(4)
其中
v=m-n+1
式中F——机构自由度
fi——第i个运动副自由度
m——运动副数
v——独立回路数n——构件数
ξLj——第j个独立回路的独立位移方程数
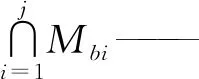
Mb(j+1)——前j+1条支链末端构件的POC集
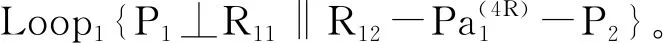
由式(3)可得第1回路的独立位移方程数ξL1为
由式(4)求得第1个子并联机构的自由度为
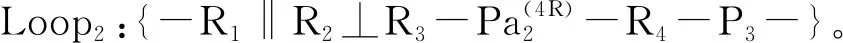
由式(3)可得其独立位移方程数ξL2为
由式(4)求得机构的自由度为
因此,该机构的自由度为3,取机架上的P1、P2、P3副为驱动输入时,机构动平台1可实现三平移输出。
1.2.3耦合度计算
由基于单开链(SOC)的机构组成原理[11]知,任一机构可分解为约束度为正、零、负的3种有序单开链(SOC),第j个SOC的约束度定义为
(5)
式中mj——第j个SOC的运动副数
Ij——第j个SOC的驱动副数
进一步,一组有序的v个SOC可划分成一个独立回路数为v的最小子运动链(Sub kinematics chain,SKC),它仅含一个零自由度BKC(Basic kinematics chain);对一个SKC而言,需
因此,耦合度为
(6)
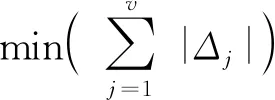
κ的物理意义在于揭示机构回路运动变量之间的关联、依赖程度;κ越大,机构的耦合程度越高,运动学、动力学的分析越复杂。
由式(5)求得第1、2回路的约束度分别为
因此,该机构包含SKC1和SKC2,其耦合度由式(6)求得为
该机构的位置求解可转换为对这两个SKC的位置求解,且由于它们的耦合度为0,无需设立虚拟变量,其位置正解可分别独立求解。
2 位置正、逆解分析
2.1 坐标系建立和参数标注
如图3所示,在静平台0上建立OXYZ坐标系,O为移动副P1、P2所在导轨的中点,X轴垂直于导轨方向所在直线,Y轴与导轨方向所在直线重合。
在动平台1上建立oxyz坐标系,o为直线D3C3的中点,x轴与直线D3C3重合,y轴与直线D3C3垂直;而Z、z轴分别由右手法则确定。
静平台0两条导轨之间的间距为M;动平台上,D3C3的长度为m,连接驱动副的3根连杆长度相等,即lA1B1=lA2B2=lA3B3=l1;平行四边形副Pa1长边长度为l3,短边长度为2l2;杆lB1C1的长度l3,lC1D1=lC2D1=l1+l4,杆件lD1D2的长度为t,杆lD2D3的长度为l5,平行四边形副Pa2长边长度为l6。
设驱动副P1、P2、P3(图3中A1、A2、A3)与原点的距离分别为S1、S2、S3。
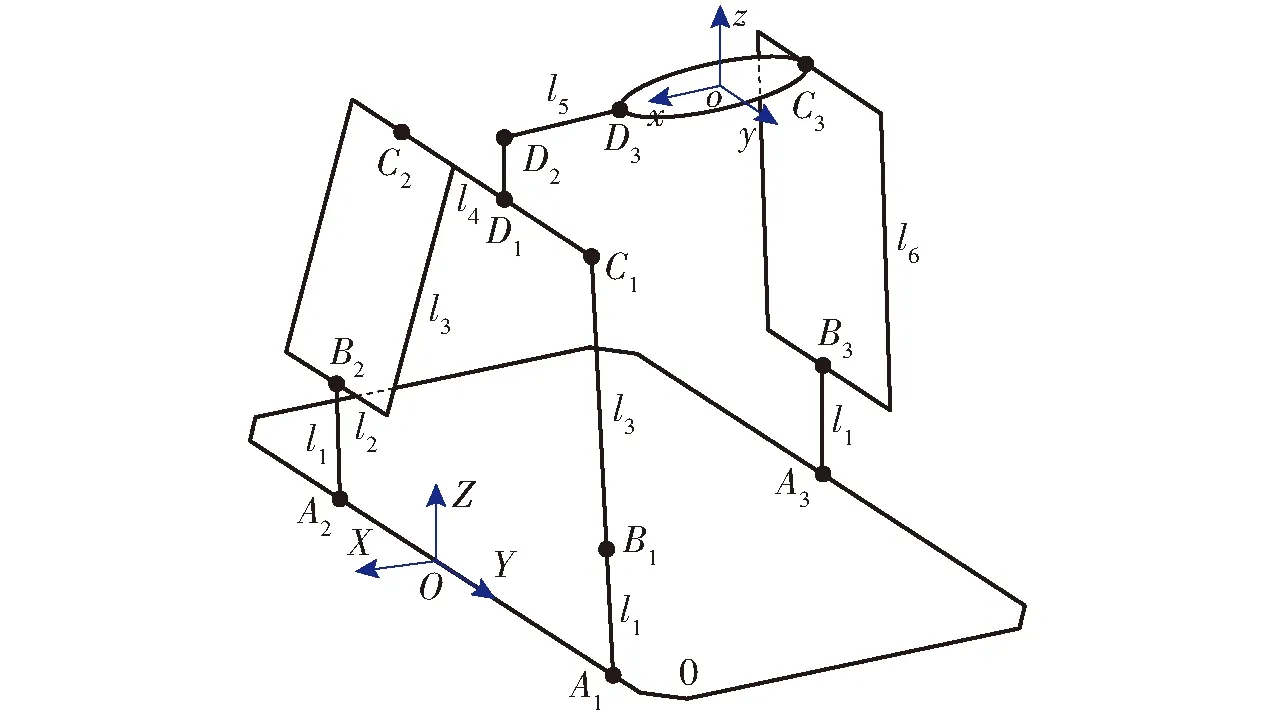
图3 机构参数标注及坐标系设定Fig.3 Mechanism parameter annotation and coordinate system setting
2.2 正向位置符号解求解
位置正解求解为:已知驱动副的行程S1、S2、S3,求解动平台o的坐标(x,y,z)。
在静坐标系中,易知点A1、A2、A3、B1、B2、B3的坐标分别为:A1=(0,S1, 0)、B1=(0,S1,l1)、A2=(0,S2, 0)、B2=(0,S2,l1)、A3=(-M,S3, 0)、B3=(-M,S3,l1)。
2.2.1SKC1的位置求解
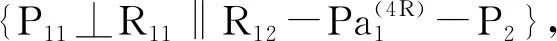
由几何约束条件lB1C1=lB2C2=l3,列出两个位置方程,求得:当S1-S2≠2(l2+l4)时,点D1坐标为
其中,另一zD1值使构型发生干涉,舍去。
当S1-S2=2(l2+l4)时,子并联机构发生奇异,失去Z方向的自由度,奇异位型如图4所示。
图4 奇异位型Fig.4 Singular configuration
2.2.2SKC2的位置求解
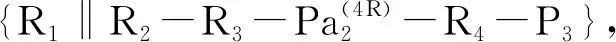
由点D1的坐标可得点D2的坐标为(0,yD1,zD1+t)。
由几何约束条件lD2D3=l5及lB3C3=l6,求得
(7)
其中
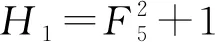
式(7)即为该机构的正向位置符号解,可表示为
(8)
由式(8)知,该机构具有输入-输出运动部分解耦性,这有利于该机构的轨迹规划和运动控制。
2.3 位置逆解求解及验证
位置逆解的求解为:已知动平台上点o的坐标(x,y,z),求解驱动副的行程S1、S2、S3。
在动坐标系oxyz中,由动平台上点o的坐标可得点C3和点D3的坐标分别为(x-m,y,z)、(x+m,y,z)。
设点D2的坐标为(0,yD2,z)。由几何约束lD2D3=l5,可得
设点D1的坐标为(0,yD1,z-t)。在SKC1中,由几何约束lB1C1=lB2C2=l3,求得移动副P1、P2的行程S1、S2分别为
(9)
由式(9)可知,S1、S2各有2组解。因此,有2×2=4种反解;其中,有2种会导致机构发生图4所示奇异,不可取。因此,机构的动平台位置确定时,机构驱动副输入S1、S2只有2组解。
在SKC2中,由几何约束lB3C3=l6,求得移动副P3的行程S3为
(10)
式(9)、(10)即为该机构的位置逆解解析式。由此可知,机构的驱动副输入S3有2组解,而S1、S2有2组解。因此,机构存在4种构型。
设机构各杆件杆长分别为:l1=55 mm,l2=40 mm,l3=160 mm,l4=35 mm,l5=80 mm,l6=200 mm,m=30 mm,M=200 mm,t=20 mm。取3个移动副的输入分别为:S1=120 mm,S2=-100 mm,S3=0 mm。将上述数值代入式(7)中,求得机构位置正解数值如表1所示。

表1 机构位置正解
取表1中的第1行数据,代入式(9)、(10)中,求得逆解数值如表2所示。
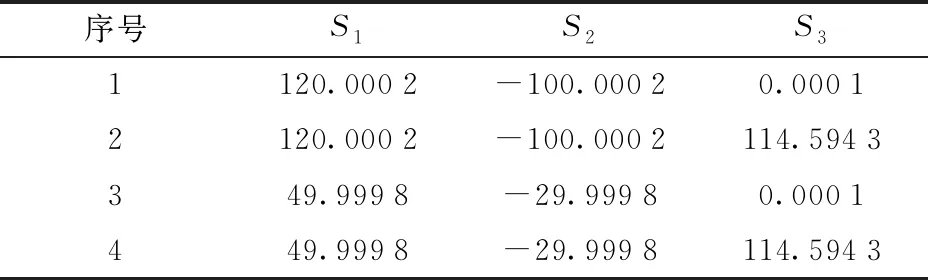
表2 机构位置逆解
结果表明,表2中第1组值与机构设定的驱动输入(S1=120 mm,S2=-100 mm,S3=0 mm)一致;验证了机构正逆解公式的正确性。
3 工作空间分析
并联机构的工作空间是在考虑杆件的干涉、移动副的行程限制、转动副或球副的转角等限制条件下,动平台上某一选定点的运动范围。
为获得该机构的工作空间,选取2.3节定义的杆长参数,设定的限制因素分别为:平行四边形副的转角为15°~165°,移动副行程范围-600~600 mm,且S2始终小于S1。采用极限边界搜索法,由Matlab软件绘制得到该并联机构的三维工作空间如图5所示,工作空间在XY、XZ截面上的视图如图6所示。
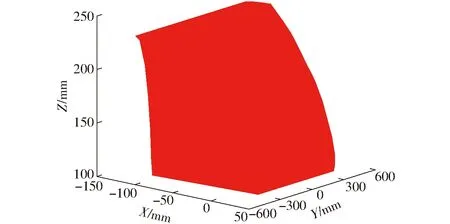
图5 工作空间的三维视图Fig.5 3D view of workspace
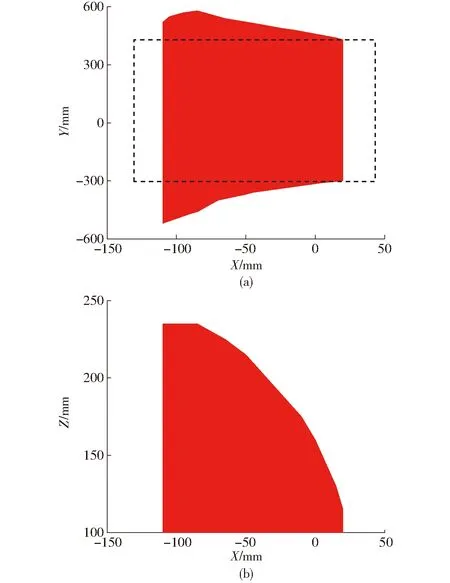
图6 工作空间在XY、XZ截面上的视图Fig.6 Views of workspace on XY and XZ sections
由图6可知,当3个驱动副行程范围有限时,该机构的部分工作空间具有Y轴方向的各向同性,即为图6a黑色线框内部工作空间。在该机构后续的性能分析中,显然,需要重点研究机构在该部分工作空间中的性能。为方便叙述,将该部分工作空间命名为规则实用工作空间。
由于该机构为移动副驱动,所以当导轨长度扩大时,工作空间也会随之扩大。因此,该机构不仅适用于小范围内的三平移精密操作,也能用于沿导轨方向的大范围内的工件搬运、抓取、喷涂等操作。
4 性能指标的分析与计算
并联机构的性能分析是为了评判机构在工作空间中是否具有良好的可操作性能。基于文献[24]提出的性能指标,评价该3T机构的输入端和输出端的运动/力传递性能。首先,基于螺旋理论求解了该机构各支链的输入传递指标(Input transmission index,ITI)和输出传递指标(Output transmission index,OTI)的表达式,然后,利用Matlab绘制机构在规则实用工作空间XZ截面的输入传递与输出传递指标曲线。
4.1 性能指标的定义
文献[24]提出的几种性能指标的定义如下:
第i个传递力旋量的输入传递指标为
(11)
式中n——支链数目
$Ti——分支i的传递力旋量
$Ii——分支i的输入运动旋量
第i个传递力旋量的输出传递指标为
(12)
式中 $Oi——分支i的输出运动旋量
为了整体评价机构输入端的运动传递性能,定义机构的输入传递指标为
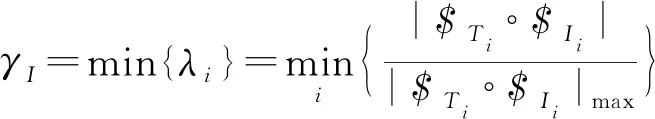
(13)
为了整体评价机构输出端的运动传递性能,定义机构的输出传递指标为
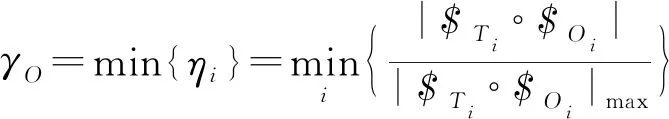
(14)
定义并联机构整体的传递指标为局部传递指标(Local transmission index,LTI)γ,有
γ=min{γI,γO}
(15)
4.2 性能指标求解
借助螺旋理论,首先,分别求解2条支链的传递力旋量与输入、输出运动旋量。然后,根据式(11)~(15),求解该机构的性能指标。
4.2.1支链Ⅰ(HSOC1)传递力的求解
在坐标系OXYZ中,首先求出支链Ⅰ中各运动副的旋量为
其中
H=S2+l2+l3cosα+l4
式中α——杆件Ra1Rd1与Y轴正向的夹角(图7)
α′——杆件R11R12与Y轴正向的夹角
θ——杆件R1R2与X轴正向的夹角
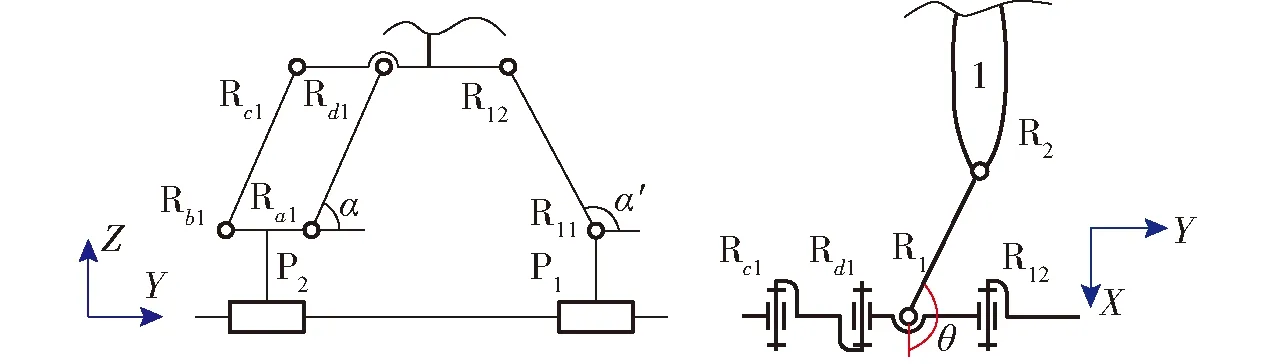
图7 支链Ⅰ的角度表示Fig.7 Angle marking of branch Ⅰ
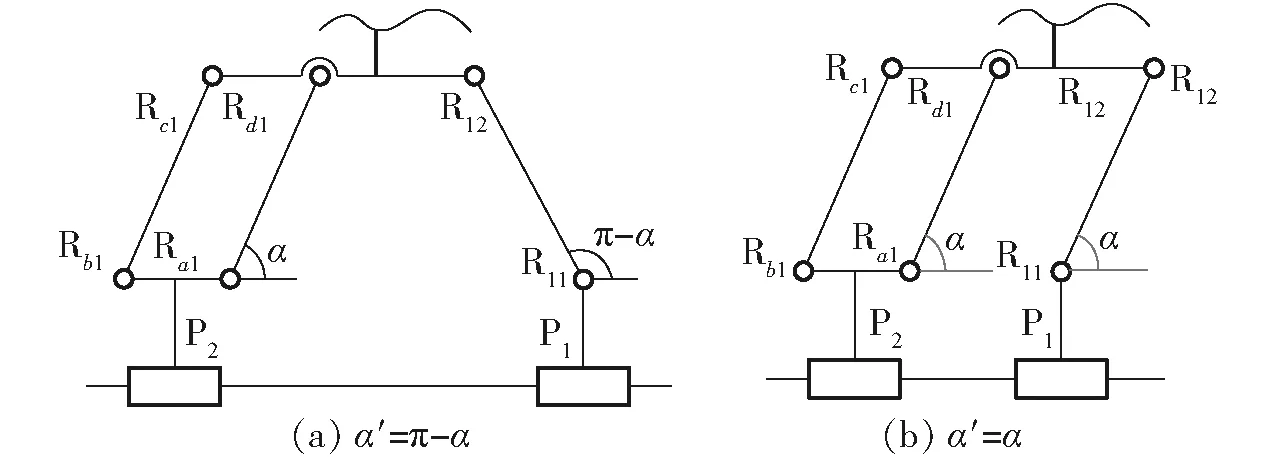
图8 子并联机构的两种构型Fig.8 Two configurations of sub parallel mechanism
研究发现,由于杆长约束与拓扑约束,α′与α存在特殊几何关系。即α′=π-α或者α′=α(2.2.1节所述奇异位型),具体位型如图8所示。因为机构处于奇异位型下其局部传递指标为0,且该种奇异在设定合适的输入条件下可以避免,因此,为分析方便,本节只研究α′=π-α构型时机构的传递性能。
由1.2.1节可知,混合支链Ⅰ末端作3T1R运动,其转动绕Z轴,则该支链的2个约束力旋量(Constrained wrench screw, CWS)分别为
根据文献[24],传递力旋量(Transmission wrench screw, TWS)为“刚化”驱动副后,与支链中其他所有运动副旋量互易积为0,且与约束力旋量线性无关。因此,先后分别“刚化”驱动副P1、P2,采用文献[25]提供的反螺旋求解方法,可求出该支链的两个传递力旋量为:
刚化驱动副P1,得到传递力旋量为
$T1=(T11,T12,T13;T14,0,T16)
其中T11=cosαcosθT12=cosαsinθ
T13=-sinαsinθT14=-sinθ(l1cosα+S1sinα)
T16=-Hcosαcosθ
刚化驱动副P2,得到传递力旋量为
$T2=(T21,T22,T23; 0, 0,T26)
其中T21=T11T22=T12T23=sinαsinθ
T26=-Hcosαcosθ
因此,支链Ⅰ的两个传递力旋量均为螺旋。
4.2.2支链Ⅱ(HSOC2)传递力的求解
在坐标系OXYZ下,分别求得支链Ⅱ包含的各运动副的运动螺旋为
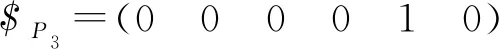
式中γ1——平行四边形副Pa2与XOY平面的夹角
β——R3R4在XOY平面的投影与X轴正向的夹角
具体角度标注如图9所示。
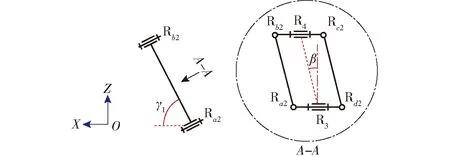
图9 支链Ⅱ角度参数Fig.9 Angle parameters of branch Ⅱ
同样,支链Ⅱ的运动也为3T1R,转动方向为绕Y轴的转动,则该支链的2个约束力旋量分别为
刚化驱动副P3,求得该支链的传递力旋量为
$T3=
(cosγ1cosβ,cosγ1sinβ,sinγ1;0,l1cosγ1cosβ-Msinγ1,0)
因此,支链Ⅱ传递力旋量表示的是轴线同时经过转动副R3、R4中点的一个纯力。
4.2.3机构输出运动旋量的求解
据文献[24],保留一个驱动,“刚化”其余所有驱动,其余的传递力也将变成约束力,那么只有该驱动的运动经过传递力$Ti的作用传递到动平台。动平台在该传递力的作用下发生相应的输出运动,可用输出运动旋量$Oi(Output twist screw, OTS)表示。根据运动旋量与力旋量的互异性,只有该驱动对应的传递力$Ti能对动平台做功,即
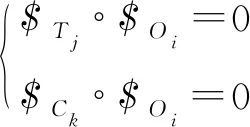
(16)
式中 $Ck——机构的第k个约束力旋量
由于机构的运动为空间3T运动,因此,动平台将受到3个方向约束力偶的作用,分别为
(17)
因此,根据式(16),由反螺旋理论[25]可求出该机构3个传递力对应的输出运动分别为
$O1=(0,0,0;L1,M1,N1)
$O2=(0,0,0;L2,M2,N2)
$O3=(0,0,0;L3,M3,0)
其中L1=cosγ1sinβsinαsinθ-cosαsinθsinγ1
M1=cosαcosθsinγ1-sinαsinθcosγ1cosβ
N1=cosαsinθcosγ1cosβ-cosαcosθcosγ1sinβ
L2=-cosγ1sinβsinαsinθ-cosαsinθsinγ1
M2=cosαcosθsinγ1+sinαsinθcosγ1cosβ
N2=N1L3=-2cosαsinθsinαsinθM3=L3
3个输出运动旋量$O1、$O2、$O3原部均为零,再次证明机构输出运动为3个不同方向的平移运动。
4.2.4性能指标图谱绘制
根据式(11)~(15),依次求解各支链的输入、输出传递指标。
支链Ⅰ的输入传递指标(ITI)为
λP1=λP2=|cosαsinθ|
支链Ⅱ的输入传递指标(ITI)为
λP3=|cosγ1sinβ|
支链Ⅰ的输出传递指标(OTI)为
ηP1=|cosγ1sinαsinθcosα(sinβcosθ-cosβsinθ)|
ηP2=|cosγ1sinαsinθcosα(cosβsinθ-sinβcosθ)|
支链Ⅱ的输出传递指标(OTI)为
ηP3=|cosγ1sinαsinθcosα(sinβcosθ-cosβsinθ)|
由式(13)得机构输入端的输入传递指标γI为
γI=min{|cosαsinθ|,|cosγ1sinβ|}
由式(14)得机构输出端的输出传递指标γO为
γO=min{η1,η2,η3}=
|cosγ1sinαsinθcosα(sinβcosθ-cosβsinθ)|
根据机构输入、输出传递指标的解析式,利用Matlab编程,绘制规则实用工作空间XZ向截面的输入、输出传递指标图,如图10、11所示。
由图10、11可知,机构在规则可用工作空间内,输入传递指标随着高度增加而逐渐减小,且最大输入传递指标为0.8;而在Z=150~200 mm之间,机构输出传递性能较好,且最大输出传递指标为0.35。图10、11中的黑色线框均表示工作空间边界。
5 奇异性研究
文献[24]将并联机构的奇异类型分为约束奇异与传递奇异,只有少自由度机构才会发生约束奇异。约束奇异分为输出约束奇异和输入约束奇异,传递奇异也可分为输出传递奇异和输入传递奇异。应用该方法分析奇异的优点在于:不需要求解并联机构雅可比矩阵;从运动和力传递角度,可清晰地揭示机构发生奇异的物理意义。基于该原理,本节将根据各支链的约束力旋量、输入、输出运动旋量的互易积,来分析该并联机构的奇异位型,并综合评价该机构的奇异特性。
5.1 机构约束奇异
当少自由度并联机构的自由度数目为n(n<6),则该机构应该存在q个约束力旋量,限制了机构另外的(6-n)个自由度[24],此时,这q个约束力旋量的最大线性无关数应为(6-n)。在机构运动过程中,若这q个约束力旋量最大线性无关数小于(6-n),则这q个约束力旋量将无法限制机构的(6-n)个自由度,则机构将必然获得额外不可控自由度,此时,即发生约束奇异。
由式(17)可看出,3个约束力偶的最大线性无关数目为3且始终为3,即机构的3个转动自由度在运动过程中始终被约束,因此,该机构不会发生约束奇异。
5.2 机构传递奇异
当传递力旋量与输入运动旋量或输出运动旋量的互易积为0时,传递力旋量无法对机构的输入运动或输出运动做功,此时,机构发生传递奇异[24]。
当$Ti∘$Ii=0时,传递力旋量不能够将输入关节的运动传递出去,则动平台将失去一个自由度,机构发生输入传递奇异。
在该机构中,传递力$T1和与其对应输入运动旋量$I1的互易积为
$T1∘$I1=cosαsinθ
(18)
由式(18)可知,机构在cosα=0或sinθ=0时,传递力$T1和与其对应输入运动旋量$I1的互易积等于0,即α=90°、θ=180°(在2.3节所述尺寸下,其他角度构型不存在,下同)时,机构发生输入传递奇异,图12为θ=180°时奇异位型。
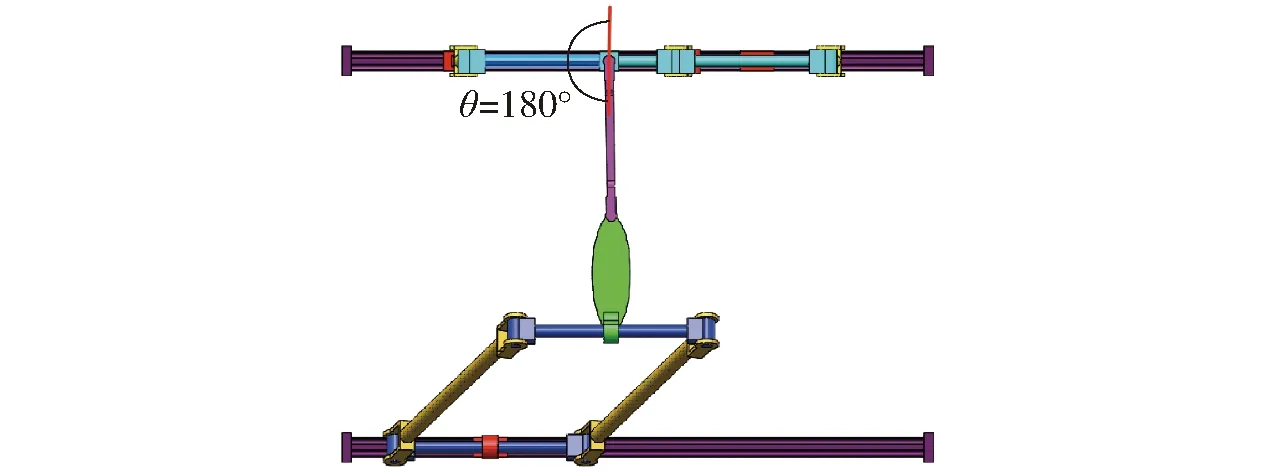
图12 奇异位型ⅠFig.12 Singular configuration Ⅰ
传递力$T2和与其对应输入运动旋量$I2的互易积为
$T2∘$I2=-cosαsinθ
(19)
由式(19)可知,传递力$T2发生输入传递奇异的条件与传递力$T1发生输入传递奇异的条件相同,故略去不作分析。
传递力$T3和与其对应输入运动旋量$I3的互易积为
$T3∘$I3=cosγ1sinβ
(20)
由式(20)可知,机构在cosγ1=0或sinβ=0时,传递力$T3和与其对应输入运动旋量$I3的互易积等于0,即γ1=90°或者β=0°时,机构发生输入传递奇异,β=0°时对应的奇异位型如图13所示。
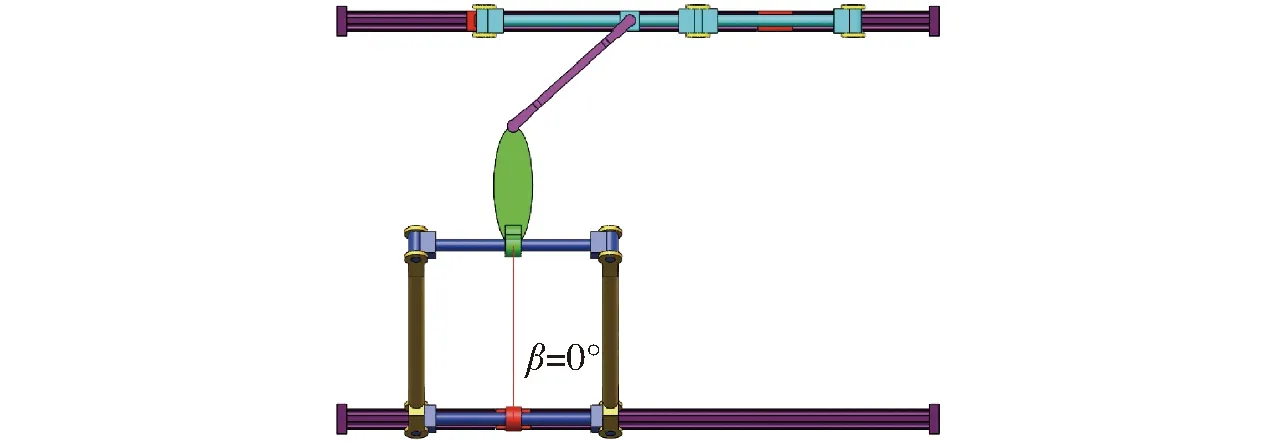
图13 奇异位型ⅡFig.13 Singular configuration Ⅱ
当$Ti∘$Oi=0时,传递力旋量无法对与之相对应的输出运动旋量做功,即该传递力不能将运动或者力传递到动平台,就会导致机构的某个自由度不可控,或者在某个方向上刚度极差,此时,机构发生输出传递奇异。
在该机构中,传递力$T1和与其对应输出运动旋量$O1的互易积为
$T1∘$O1=sin(2α)cosγ1sinθsin(β-θ)
(21)
由式(21)可知,机构在sin(2α)=0、sinθ=0、cosγ1=0或sin(β-θ)=0时,传递力$T1和与其对应输出运动旋量$O1的互易积为0,即α=90°,θ=180°,γ1=90°,机构发生输出传递奇异,图14为α=90°与之对应的奇异位型。
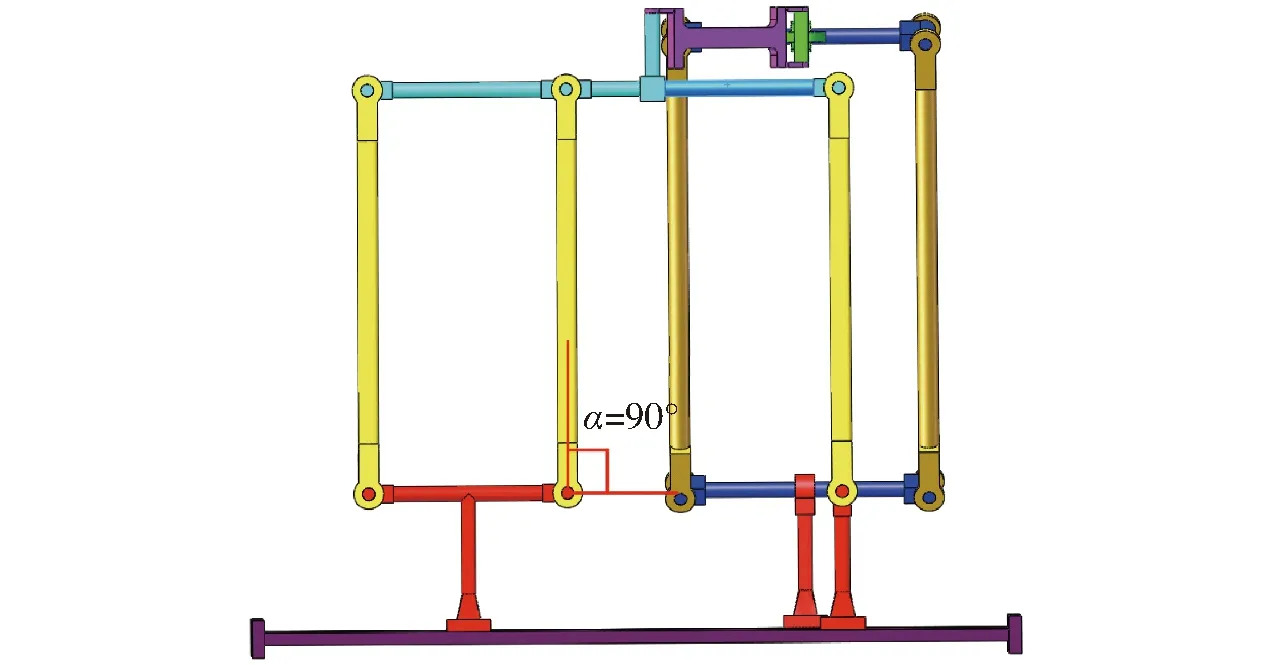
图14 奇异位型ⅢFig.14 Singular configuration Ⅲ
经分析,传递力$T2、$T3与其对应的输出传递运动$O2、$O3的互易积,与传递力$T1和与其对应输出运动旋量$O1的互易积为0相同,即发生奇异的条件相同,故略去不作分析。
5.3 机构距离奇异位型的远近评价
并联机构处于奇异位型及其附近区域时,其运动和力/约束传递性能较差。因此,利用Matlab绘制机构在规则实用工作空间XZ截面局部传递指标(LTI)图,以此观察机构在该空间内部距离传递奇异的远近,评价机构奇异特性。
由图15可知,规则实用工作空间内部最大局部传递指标(LTI)为0.3,分布于{(X,Z)|-70 mm 图15 规则实用工作空间XZ截面LTI分布曲线Fig.15 LTI distribution curve of XZ section of regular practical workspace 因此,LTI在规则实用工作空间内部都大于0,即该机构在其内部不存在奇异。 当子并联机构构型为α′=α时(图8b),求得此时机构的输出运动旋量$O1、$O2、$O3分别为 $O1=$O2=(0, 0, 0;L1,M1,N1) 根据文献[19]定义的奇异类别,机构该种奇异类型为输出传递奇异,即失去一个方向的自由度。 (1)基于POC理论设计了一种具有正向位置符号解的新型3T机构,该机构仅由移动副和转动副组成,易于制造和安装;因机构的耦合度κ=0,具有正向位置符号解,有利于进行误差分析、尺度综合、刚度分析及动力学研究等;具有部分输入-输出运动解耦性,有利于机构的轨迹规划及运动控制;移动副为驱动,操作工作空间大,可适用于长度方向较大尺寸工件的机加工、喷涂、铆接等工艺;平行的导轨布置方式使部分工作空间具有各向同性,有利于机构的性能分析。 (2)将机构的运动/力传递性能指标应用于含混合支链的本文机构的运动/力性能分析,选取了具有Y向各向同性的部分工作空间,进行传递性能指标及奇异特性的分析,分析了机构的奇异位型,得到了局部传递指标曲线,可观测机构距离传递奇异位型的远近,且在选定合适的输入时,该机构的所有类型奇异全部位于工作空间的边界,无奇异工作空间较大。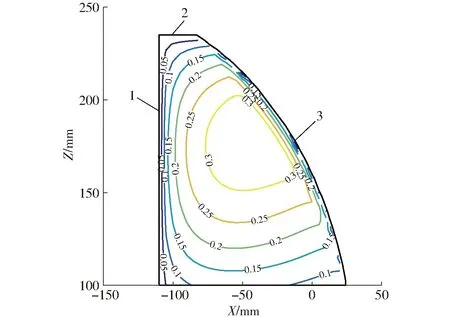
5.4 子并联机构α′=α构型奇异归类
$O3=(0, 0, 0; 0, 0, 0)6 结论

