高地隙自走式喷雾机多模式液压转向系统设计与试验

扈 凯 张文毅

(农业农村部南京农业机械化研究所， 南京 210014)

0 引言

传统的植保机械农药利用率低、作业效率低、劳动强度大，难以满足大田种植的要求[1-2]。新型高地隙自走式喷雾机可大规模应用于大豆、甘蔗、玉米等高秆作物的全程施药作业，是一种较为理想的大田植保机械[3-5]。现有高地隙喷雾机大多采用前轮转向，部分机型采用四轮转向，由于其整车体积大、重心高，使得高地隙喷雾机在换行、掉头、转场过程中机动性较差[6-10]。因此，迫切需要对高地隙自走式喷雾机的多模式转向系统进行研究。

国外自20世纪70年代就开始研发高地隙自走式喷雾机[11-13]。John Deere公司研发的JD4730型高地隙自走式喷雾机采用前轮转向方式，离地间隙1.5 m；Case Crop公司生产的Patriot 4430型喷雾机采用全液压驱动系统、四轮液压助力转向。近年来，国内逐步开展对高地隙自走式喷雾机的研究，其转向系统大多采用前轮转向或四轮转向[14-19]，尚未见兼顾前轮转向和四轮转向优势的产品。李伟等[20]研制了一种高地隙自走式喷雾机的多轮转向系统，构建了转向系统的数学模型，并通过Matlab/Simulink进行了仿真；夏长高等[21]对高地隙自走式喷雾机的四轮转向系统进行了研究，并对转向系统的动态特性进行仿真分析；毛罕平等[22]研究了高地隙液压四轮驱动喷雾机的转向防滑控制系统，对控制系统在不同转向角下的控制精度进行了试验验证。

为解决高地隙自走式喷雾机实际使用过程中的问题，本文研究一种可实现前轮转向、四轮转向的多模式液压转向系统，通过采用PID控制策略实现转向系统较高的转向精度，并对液压系统的主要参数进行设计和计算。同时，基于AMESim软件构建液压-机械耦合模型，采用序列二次组合优化算法确定PID参数的最佳组合，并对不同负载力和负载质量下系统控制精度进行仿真。通过多模式转向系统实车测试平台，在坡度15°土路和田间进行转向系统性能测试，以期为多模式液压转向系统的设计提供理论基础。

1 转向系统动力学分析

1.1 前轮转向

图1为前轮转向车辆向左转向过程中的状态。在较慢的行驶速度下，内侧转向轮和外侧转向轮之间存在一个运动学条件，满足该条件时，车轮可以实现无滑移转向，该条件被称为阿克曼条件。前轮转向的阿克曼条件表示为

(1)

式中θof——前轮外侧车轮转向角，(°)

θif——前轮内侧车轮转向角，(°)

Wf——前轮轮距，mm

L——车辆轴距，mm

阿克曼条件在车速较低且侧偏角接近于0时适用，这种情况下，没有相互平衡的侧向力和离心力。

图1 前轮转向系统示意图Fig.1 Schematic of front wheel steering system

1.2 四轮转向

图2为异相位四轮转向车辆向左转向过程中的状态，异相位是指在转向过程中，前轮和后轮的转向方向相反。

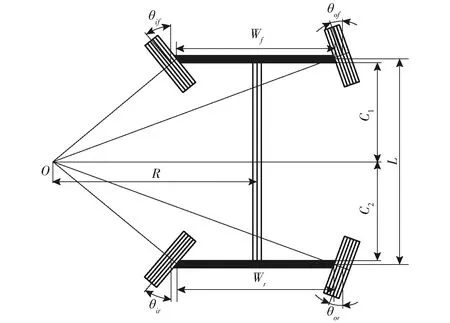
图2 四轮转向系统图Fig.2 Schematic of four wheels steering system

根据几何关系，可以推导出各个轮子的转向角计算公式

(2)

(3)

(4)

(5)

式中θir——后轮内侧车轮转向角，(°)

θor——后轮外侧车轮转向角，(°)

Wr——后轮轮距，mm

C1——转向中心到前轮轴线的垂直距离，mm

C2——转向中心到后轮轴线的垂直距离，mm

R——转向中心到质心的垂直距离，mm

对于高地隙自走式喷雾机，四轮转向采用对称转向方式，即内侧两个车轮转向角大小相同、方向相反，外侧两个车轮转向角大小相同、方向相反。

通过上述分析可知，虽然四轮转向半径更小，但由于其转向中心上移，在机器正前方空间不足的情况下，四轮转向系统的转向通过性不如前轮转向。但四轮对称转向系统前后轮子同轮辙，减少对作物的损坏是两轮转向方式不具备的。所以，研究一种高地隙自走式喷雾机的多模式转向系统具有实际意义。

2 液压系统设计

2.1 方案制定

根据高地隙自走式喷雾机对转向系统的使用需求，设计了基于负载敏感原理和压力补偿原理的全液压转向系统，该转向系统可以实现前轮转向、四轮转向两种模式，其液压系统原理如图3所示。

图3 多模式转向液压系统原理图Fig.3 Schematic of multi-mode steering hydraulic system1.油箱 2、5.过滤器 3、6.液压泵 4、7.安全阀 8.溢流阀 9.优先阀 10.液压转向器 11.前轮转向液压缸 12.固定节流口 13.单向阀 14.蓄能器 15.两位两通换向阀 16.摩擦制动器 17.定差减压阀 18.三位四通电磁换向阀 19.梭阀 20.液控单向阀组 21.后轮转向液压缸

该液压系统主要由液压泵、优先阀、液压转向器、转向油缸、后轮转向控制阀组、制动系统控制阀组等元器件构成。液压泵3为前轮液压转向系统的动力元件，液压泵3的输出油液经优先阀的CF油口进入液压转向器。方向盘未转动时，转向器的阀芯和阀套处于中间位置，方向盘转动时，阀芯和阀套的相对位置发生改变，油液通过计量马达进入转向液压缸工作。优先阀配合负载敏感型液压转向器使用，LS油口可实时获取系统工作压力，优先阀优先保证转向器油路的流量要求，且该流量不受负荷压力变化的影响，此外，液压泵3输出的流量，除供给转向器正常工作所必需的流量外，剩余部分可全部经EF油口供给液压制动系统，从而消除了由于供油过多造成的功率损失，提高了系统效率，降低了系统发热。后轮液压转向系统由液压泵6提供动力，定差减压阀、三位四通电磁换向阀和梭阀共同组成后轮转向系统控制阀组，定差减压阀配合梭阀使用实现压力补偿，梭阀可将高压油路的压力引入定差减压阀弹簧腔一侧，确保三位四通电磁换向阀的流量不受负载大小的影响，而仅与其开度相关，进一步提高了系统的控制精度。液控单向阀组用于在后轮转向液压缸不工作时将液压缸位置锁死。前轮和后轮转向液压缸均采用双活塞杆双作用式对称液压缸。

在前轮转向模式下，控制后轮转向的液压回路不工作，在四轮转向模式下，安装在前后转向液压缸的位移传感器将液压缸位移信息反馈给控制器，控制器经过PID控制算法，使得后轮液压缸与前轮液压缸保持同步，以实现四轮转向。该控制方式可以确保在前轮转向切换至四轮转向的过程中，即使前轮未回正(方向盘处于转向的位置)，系统依然可以根据液压缸位移信息将后轮调整至适当位置。

2.2 转向系统负载计算

高地隙自走式喷雾机转向阻力矩计算参照Taborek公式

(6)

式中M——转向阻力矩，N·m

G——喷雾机满载时所受重力，取20 000 N

μ——综合摩擦因数，取0.85

i——轮胎中心与地面接触点至销与地面交点的距离，取0.24 m

K——当量半径，等于轮胎宽度的三分之一，取0.04 m

经计算可知，转向阻力距为4 136 N·m。

初始转向时，液压缸拉(推)动车轮左(右)转向时转向机构受力完全对称，以右转弯前后转向机构受力为例，受力分析如图4所示。

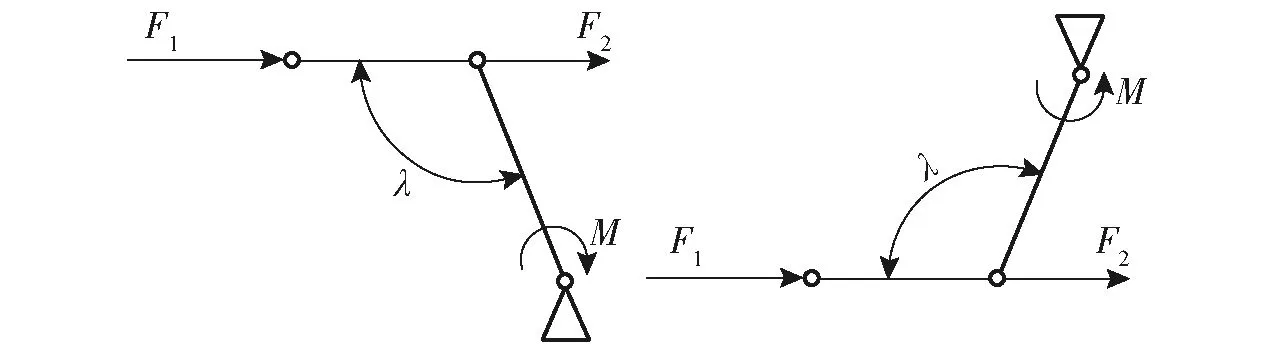
图4 前、后轮转向机构受力分析图Fig.4 Schematic of force analysis of front and rear steering mechanism

由图4可推导出前后转向液压缸活塞杆的受力公式

(7)

式中λ——连杆与转向节臂夹角，取105°

Lef——连杆长度，取0.30 m

F1——左连杆受力，N

F2——右连杆受力，N

左右连杆受力等于转向液压缸负载力，经计算为14 273.0 N。

2.3 液压元件参数计算

根据开式液压系统负载、液压元件高效工作区等因素，参考液压设计手册，系统的设计压力选为8.0 MPa，液压缸杆径比0.5，无回油背压。

液压缸活塞直径计算公式为

(8)

式中D1——液压缸活塞直径，mm

F——转向液压缸负载力，取14 000 N

ncm——液压缸效率，取0.85

p——液压缸主工作腔压力，取8 MPa

φ——液压缸杆径比，取0.5

转向系统最大流量计算公式为

(9)

式中d——液压缸活塞杆直径，mm

v——液压缸最大运动速度，取100 mm/s

Qmax——系统最大流量，L/min

经计算并适当圆整后，液压缸活塞直径为60 mm、液压缸活塞杆直径为30 mm，系统最大流量为12.73 L/min。

3 基于AMESim的液压系统仿真

3.1 仿真模型构建

根据液压系统原理和设计参数，建立AMESim机械-液压仿真耦合模型如图5所示。

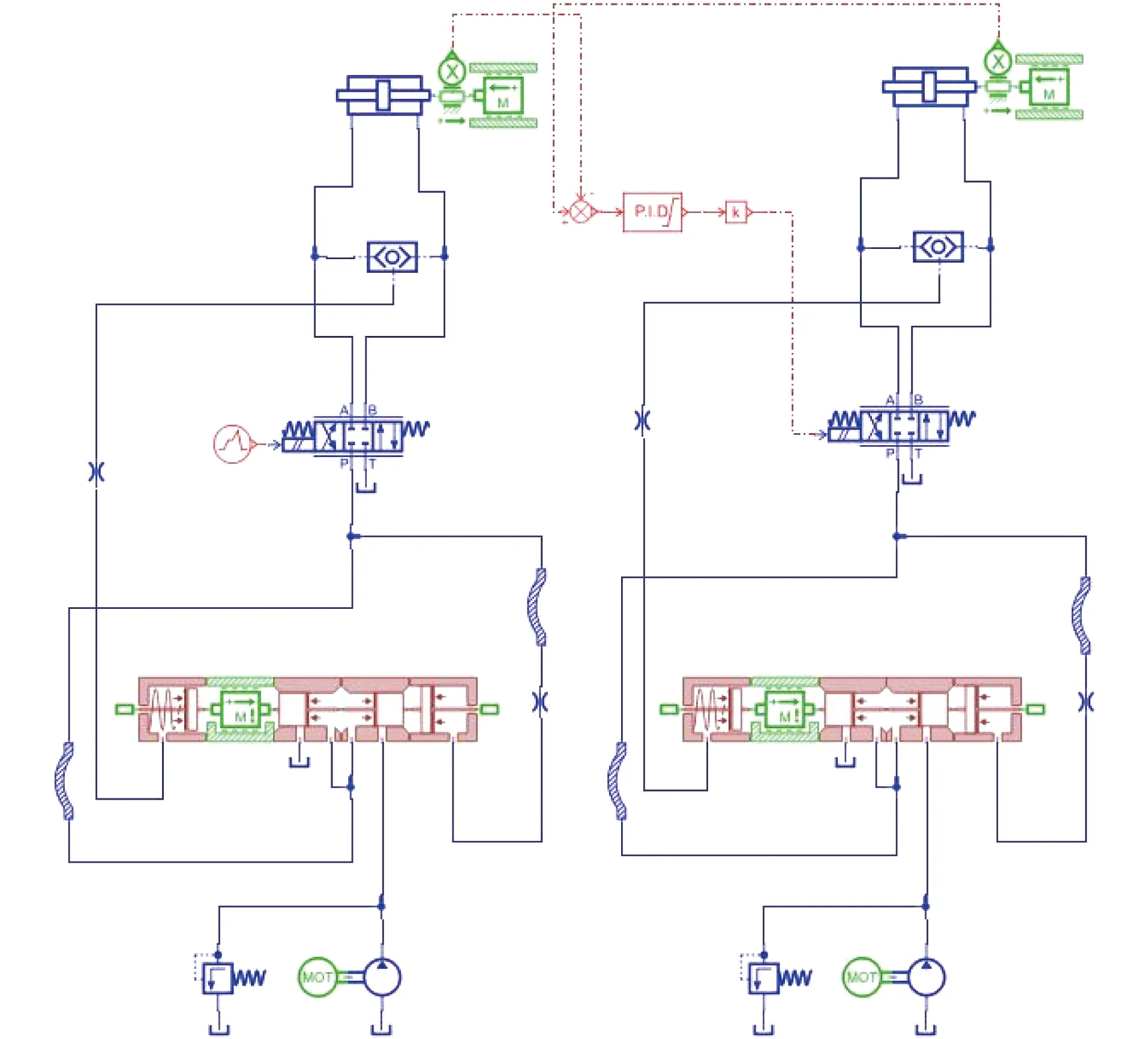
图5 AMESim仿真模型Fig.5 AMESim simulation model

液压系统通过可变节流口的流量计算公式为

(10)

式中Q——通过节流口流量，L/min

Cq——流量系数

γ——油重度

A——节流口面积，cm2

g——重力加速度，9.8 m/s2

Δp——上下游压力差，MPa

由式(10)可知，在可变节流口开度一定的情况下，其通过的流量与可变节流口上下游压力差的二分之一次方成正比，若能保持可变节流口上下游压力差恒定，系统流量仅与可变节流口开口面积成正比。压力补偿系统的引入确保了三位四通比例换向阀的通过流量仅与电信号相关，避免了因执行元件负载变化造成速度难以控制的问题。

3.2 PID参数整定

为进一步提高前后轮转向液压缸的控制精度，采用PID控制算法。比例控制为偏差与比例系数的乘积组成，这是PID控制中最基本的控制量，积分作用与偏差对时间的积分、积分时间有关，加入积分作用后，系统波动加大，但可以消除余差，微分作用与偏差对时间的微分以及微分时间有关，起补偿作用，使系统保持稳定。在PID控制算法中，比例系数、积分时间常数、微分时间常数往往通过试凑和经验来取值，本文通过序列二次组合优化算法(NLPQL)寻找PID参数的最优组合。

以前轮转向液压缸和后轮转向液压缸的位移误差最小值为目标函数，以PID控制算法的比例系数P、积分时间常数I、微分时间常数D作为优化变量，目标函数T与约束条件C表示为

T=De(P,I,D)

(11)

(12)

式中De——前轮转向液压缸和后轮转向液压缸的位移误差最小值，mm

经过NLPQL算法计算可知，当比例系数为19.087、积分时间常数为2.008、微分时间常数为0.032时，目标函数最小。仿真时间设定为5.0 s，计算步长0.005 s，在0～2.5 s时间内，前轮转向液压缸左腔进油，在2.5～5.0 s时间内，前轮转向液压缸右腔进油，前轮转向液压缸左、右腔压力变化如图6所示，不同PID取值下前轮转向液压缸和后轮转向液压缸的位移误差曲线如图7所示。

图6 液压缸左、右腔压力变化曲线Fig.6 Variation curves of left and right chamber pressure of hydraulic cylinder

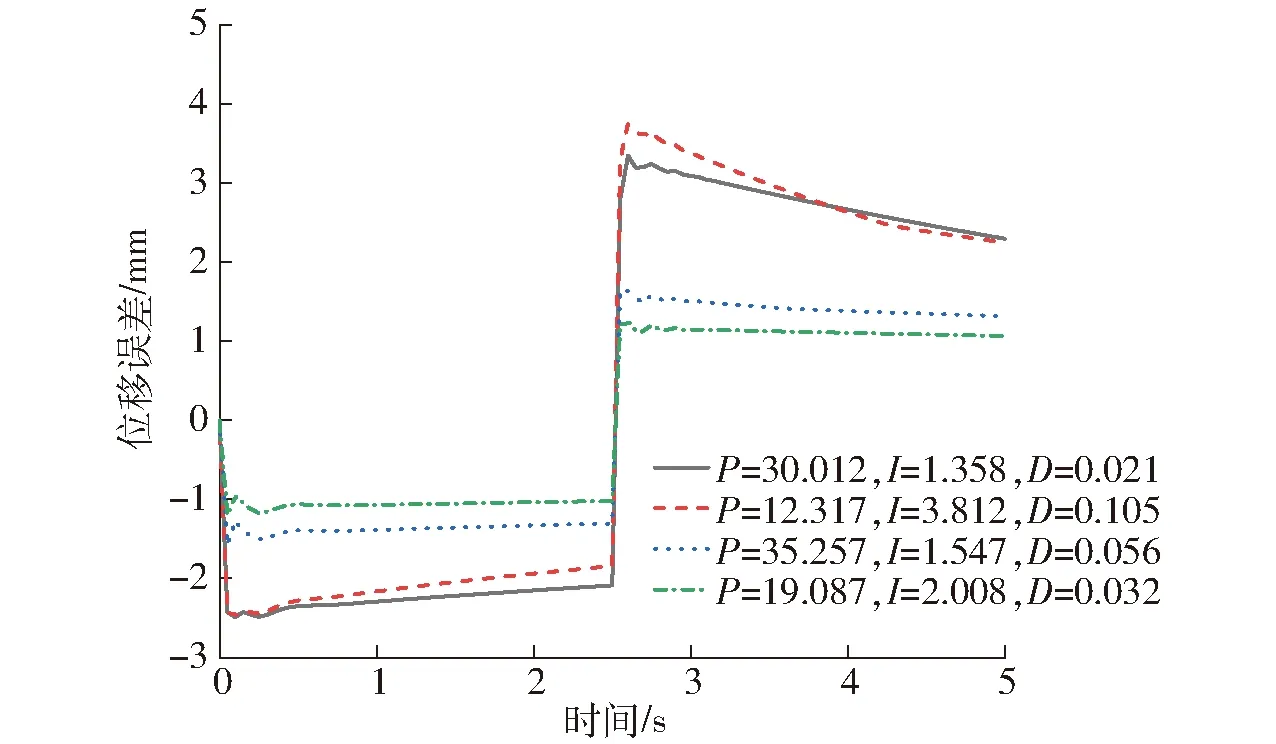
图7 不同PID参数下前后液压缸的位移误差变化曲线Fig.7 Variation curves of displacement error between front and rear hydraulic cylinders at different PID parameters

由图6可知，在0～2.5 s时间内，液压缸左腔进油，左腔压力快速上升至7.8 MPa，右腔的液压油直接流回油箱。在2.5 s时刻，三位四通电磁换向阀换向，液压缸右腔压力快速上升至7.8 MPa，左腔压力降至零。在系统初始时刻和换向后，系统压力出现了小范围的波动，随后快速趋于稳定。系统设计压力(8.0 MPa)与工作压力(7.8 MPa)基本一致，验证了系统参数的正确性。由图7可知，当PID参数设定为NLPQL算法计算的最佳组合时，两液压缸位移误差较小，无论液压缸往哪个方向运动，误差绝对值均稳定在1.2 mm。

3.3 不同负载力下的仿真分析

在实际转向过程中，由于路面条件、实际重心位置等因素的影响，前后轮转向液压缸的负载力不会时时相等，为分析不同负载力对转向系统控制精度的影响，在AMESim软件中将后轮的负载力变化设置如图8所示，前轮负载力始终保持为2.2节所计算出的液压缸外负载力(14 000 N)，系统在2.5 s时刻换向，仿真时间与仿真步长设置与上文一致。位移误差变化如图9所示。

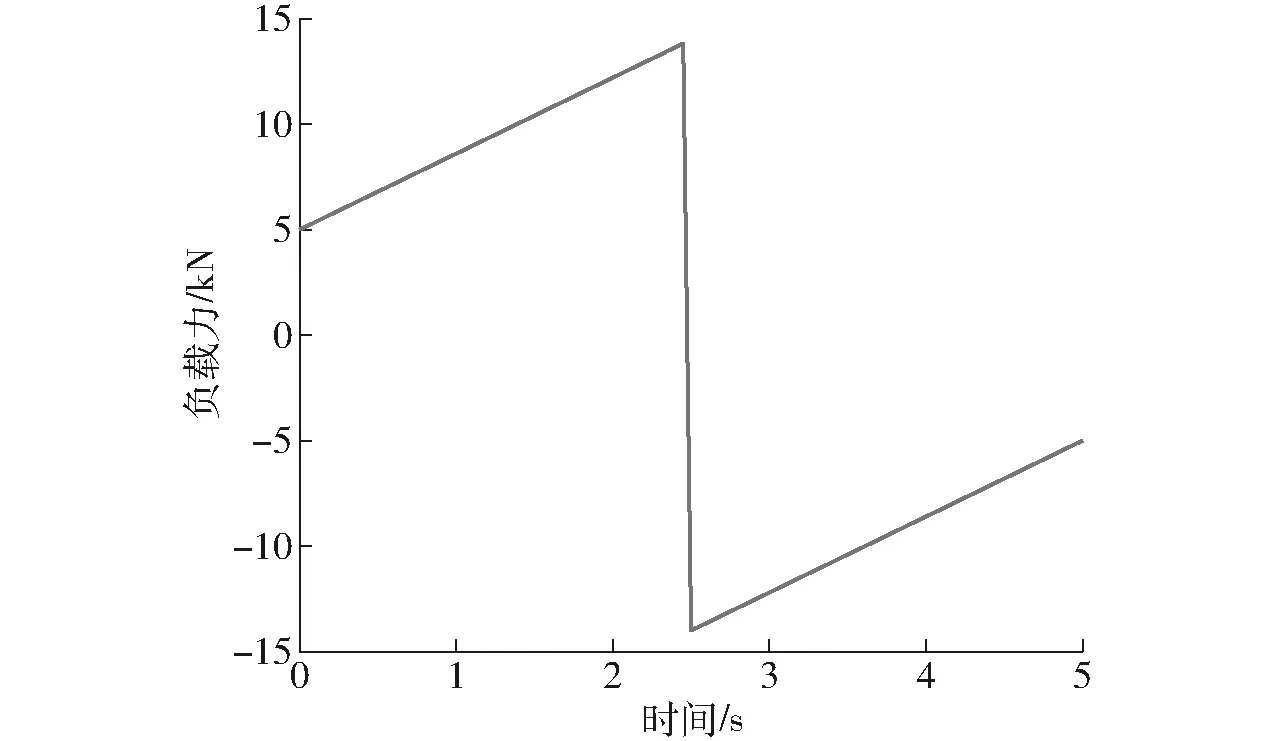
图8 后转向液压缸负载力变化曲线Fig.8 Variation curves of loading force of rear steering hydraulic cylinder

图9 不同负载力下前后液压缸位移误差变化曲线Fig.9 Variation curves of displacement error between front and rear hydraulic cylinders at different loading forces

由图9可知，当负载不同时，位移误差变大，位移误差负向最大值出现在2.5 s，为-2.18 mm，此时，液压缸运动方向转换后，位移误差出现正向最大值，为1.72 mm。虽然前、后转向液压缸负载力差值较大，但压力补偿系统和PID控制算法仍可保证两者具有较高的同步精度。

3.4 不同负载质量下的仿真分析

在AMESim软件中，转向液压缸负载力是通过添加质量块的静摩擦力和库伦摩擦力来施加的，质量块质量代表转向液压缸负载质量(主要指转向系零部件的质量)，该参数表征负载的惯量大小，对系统稳定性有一定的影响。在AMESim软件中，将负载质量分别设置为10、50、90 kg，前后转向液压缸负载均设置为14 000 N，系统在2.5 s时刻换向，仿真时间与仿真步长设置与上文一致。不同负载质量下的前后转向液压缸位移误差变化如图10所示。

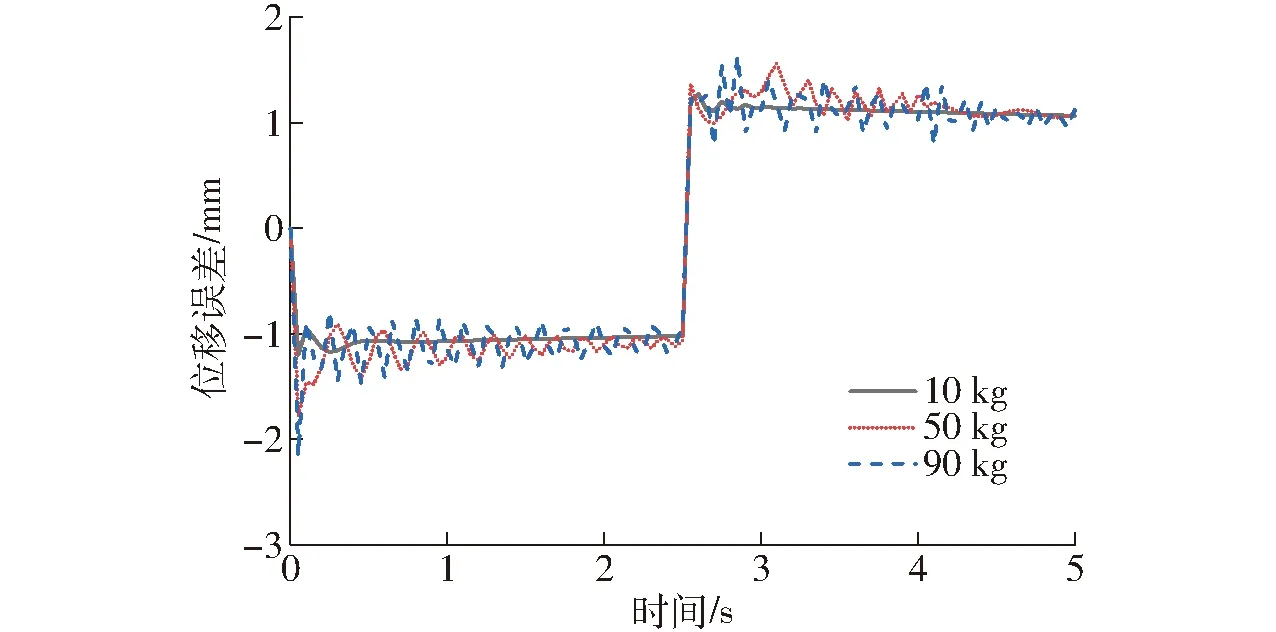
图10 不同负载质量下前后液压缸位移误差变化曲线Fig.10 Variation curves of displacement error between front and rear hydraulic cylinders at different loading masses

由图10可知，随着负载质量的增加，位移误差加大，且波动程度增大。当负载质量为10 kg时，位移误差快速稳定，除初始时刻和换向后的短暂时间内，其它时间基本没有波动。当负载质量为50 kg时，位移误差在0～2.5 s时间内始终处于小范围波动，在2.5 s后波动程度加剧，4.0～5.0 s，逐渐趋于稳定。当负载质量为50 kg时，位移误差最大，且始终处于波动状态。因此，应降低转向系统质量，轻量化设计，以提高系统的稳定性。

4 试验

4.1 试验平台搭建

为分析验证所设计的多模式转向系统的性能，研究多模式转向系统实车测试平台，选用WFS1000型拉线式位移传感器测量前后转向液压缸的位移信息，量程为1 000 mm，输出信号4～20 mA。选用Smacq 3132型16通道数据采集卡采集传感器信息，并通过USB通信方式传输给上位机，采样频率10 Hz，分辨率16 bit。在实际使用过程中，使用KB1-31型隔离变送器将传感器信号分别等值传送给控制器和数据采集卡，控制器的PID参数按照软件仿真获取的最优组合配置。多模式转向系统实车测试平台如图11所示。

图11 多模式转向系统测试平台Fig.11 Test platform of multi-mode steering system

4.2 转向系统性能测试

试验条件设置如下：①在田间和坡度15°干硬土路分别测试。②高地隙自走式喷雾机行驶速度约为2.5 km/h。③采用四轮转向模式。④驾驶员先向左边转动方向盘，然后方向盘回正，再向反方向转动方向盘，最终再使方向盘回正。需要指出的是，在坡度15°的测试中，由于喷雾机产生倾斜，且药液和肥料会因机体倾斜向一侧转移，这会造成各个轮子所承受压力不同，故在坡度15°上的转向测试可有效验证前后轮液压缸不同负载下的转向性能。

试验过程中进行多次测试，前后液压缸的位移误差基本相同，选取其中一组试验测试数据如图12、13所示。

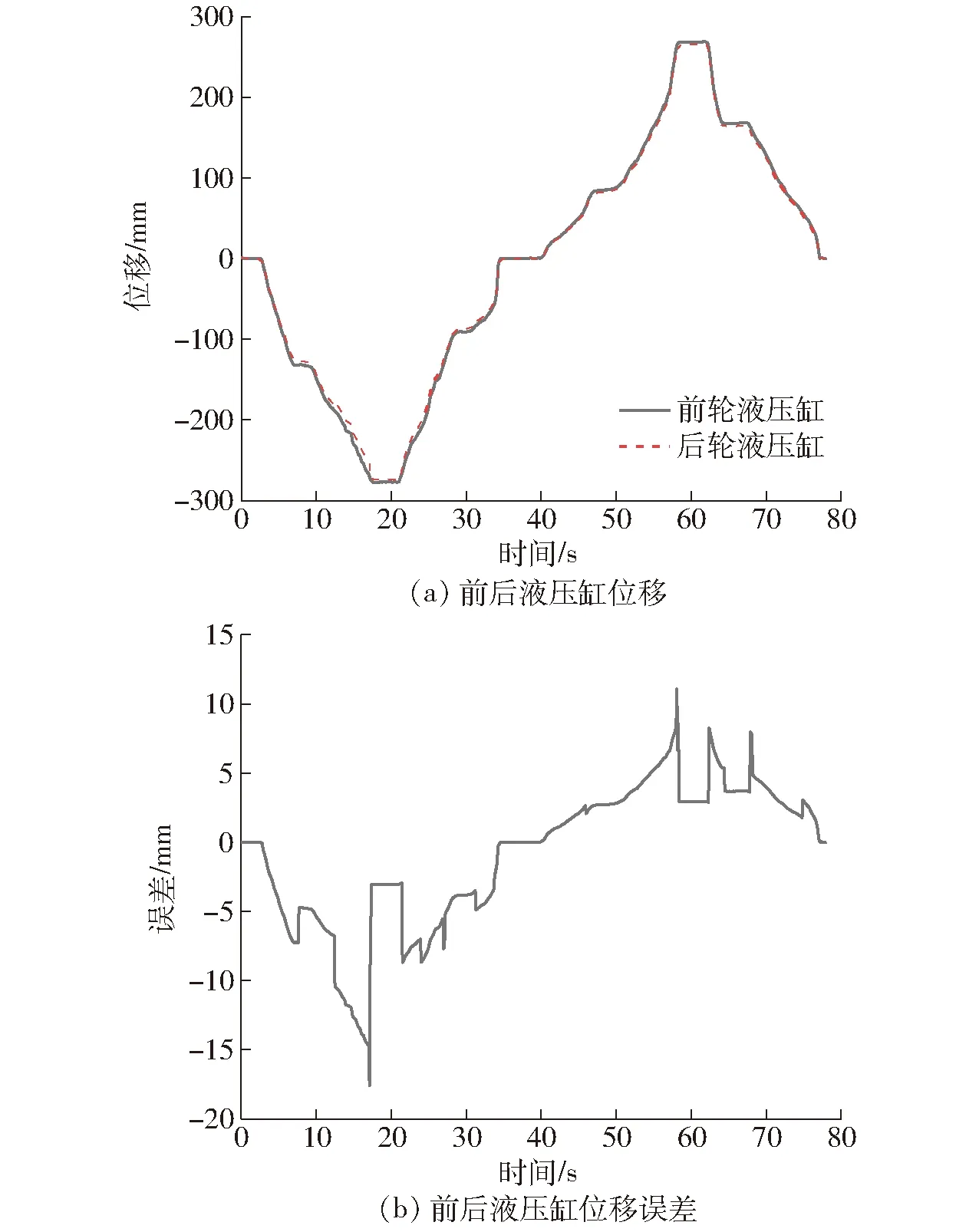
图12 田间试验结果Fig.12 Field experiment result

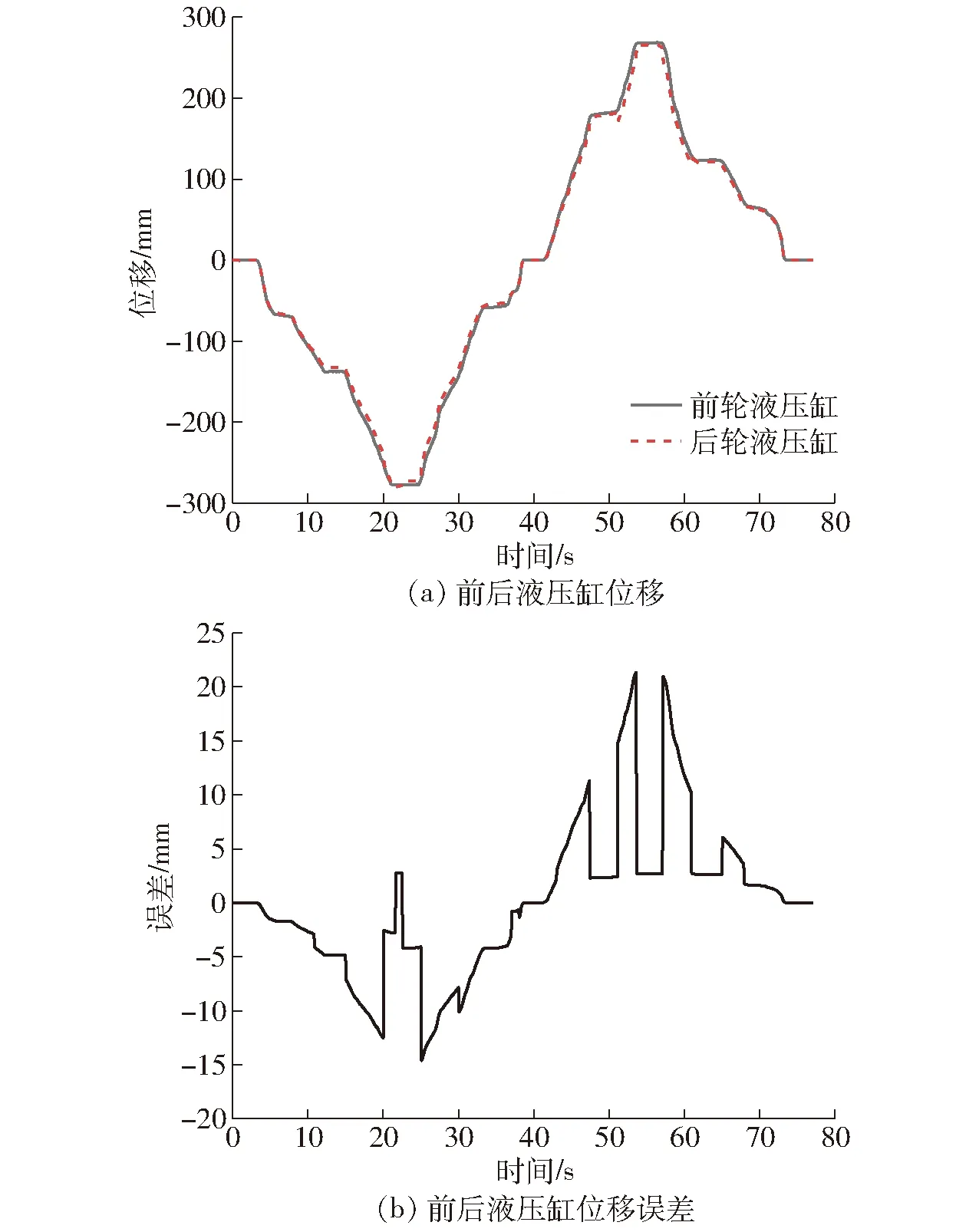
图13 坡地试验结果Fig.13 Experiment result on slope road

平均误差的计算公式为

(13)

n——总采样点数

Di——各个采样点数据的位移误差，mm

由图12可知，在田间试验时，前后轮转向液压缸之间平均误差为4.07 mm，在17.1 s负向误差最大，为-17.59 mm，在58.1 s正向误差最大，为11.10 mm。由图13可知，在坡地试验时，前后轮转向液压缸之间的平均误差为4.89 mm，在25.1 s负向误差最大，为-14.62 mm，在53.6 s正向误差最大，为21.34 mm。

为进一步验证转向系统的性能，对高地隙喷雾机进行田间转向测试，测试现场如图14所示。由理论分析可知，前轮转向模式下，外前轮转向半径计算公式为

(14)

式中Rf——两轮转向模式下转向半径，mm

四轮转向模式下，外轮转向半径计算公式为

(15)

式中Ra——四轮转向模式下转向半径，mm测量时，每组数据均测量3次，取平均值。不同外前轮转角下转弯半径数据如表1所示。

图14 田间转向试验Fig.14 Steering experiment in field

由表1可知，在两轮转向和四轮转向模式下，转向半径的实测值均大于理论值，且随着外前轮转向角的增加，误差率增大，这主要是由于在田间转向过程中轮子存在一定程度的滑转所导致的，转向角越大，滑转越明显。总体上，转向系统误差率均低于4.0%，满足设计要求。

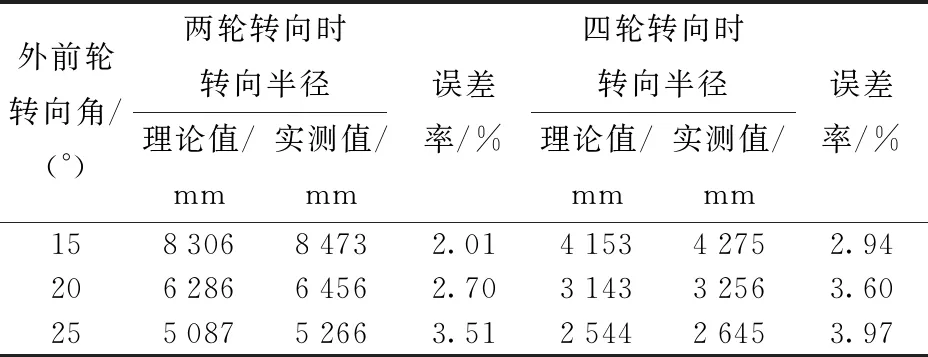
表1 不同外前轮转角下转弯半径试验结果Tab.1 Experiment results of steering radius at different steering angles of outer front wheel

5 结论

(1)在分析前轮转向和四轮转向动力学的基础上，设计了一种高地隙自走式喷雾机多模式液压转向系统。制定了液压系统技术方案，利用负载敏感优先阀控制前轮转向液压缸的控制元件，在优先保证前轮转向供油的基础上还可为其他执行元件提供动力，提高了系统效率。后轮采用定差减压阀和梭阀构成压力补偿系统，确保三位四通电磁换向阀的流量不受负载的影响，提高了系统的控制精度。采用PID控制算法确保前、后转向液压缸的同步精度，实现前轮转向和四轮转向两种转向模式。

(2)基于AMESim软件构建机械-液压转向系统耦合模型，采用序列二次组合优化算法确定PID参数的最佳组合，当比例系数为19.087、积分时间常数为2.008、微分时间常数为0.032时，前后液压缸位移误差最小。对不同负载力、不同负载质量下系统的控制特性进行了仿真分析，结果表明：当负载不同时，位移误差变大，但最大误差仅-2.18 mm，PID控制算法和压力补偿系统确保了变载荷下系统的控制精度；负载质量越大，位移误差和波动越大，应轻量化设计转向系统。

(3)在坡度15°的干硬土路和田间进行了转向系统性能测试，试验表明：田间试验时，前后轮转向液压缸之间的平均位移误差为4.07 mm，最大误差为-17.59 mm；在坡度15°的干硬土路上，前后轮转向液压缸之间的平均位移误差为4.89 mm，最大误差为21.34 mm。

(4)在不同转向模式下试验测量了田间转向半径，测试表明，在前轮转向和四轮转向模式下，转向半径的实测值均略大于理论值，且随着外前轮转向角的增加，转向半径误差率增大，但误差率均小于4.0%。试验结果验证了所设计的转向系统具有较高的控制精度和稳定性。