农田平地机导航侧滑估计与自适应控制方法

景云鹏 刘 刚 金志坤

(1.中国农业大学现代精细农业系统集成研究教育部重点实验室， 北京 100083； 2.中国农业大学农业农村部农业信息获取技术重点实验室, 北京 100083)

0 引言

在农业领域自动导航技术多用于农田生产过程[1]，通过对拖拉机和平地铲的自动控制，实现农田平地机的自动导航，可大大降低操作者的工作强度，具有较高的研究开发价值。

国内外对农田平地机导航控制的研究较少，一些国外公司例如Trimble和John Deere研发了用于各种农业生产作业的导航系统，但缺少针对农田平地机导航系统的开发。国内学者多侧重于对平地导航路径进行规划设计。文献[2-3]根据地势分布，对平地导航的全局作业路径进行合理规划。文献[4]通过拉力传感器实时获取平地铲的负载，引导驾驶员辅助导航平地作业。与自动插秧机[5-6]、施肥机[7]和直播机等不同，农田平地机的自动导航不仅需要关注其导航行驶过程中平地铲的位姿变化，还应关注平地铲能否对事先规划好的农田平整路径进行有效追踪。目前，农田平地机的拖拉机与平地铲的连接模式主要分为三点悬挂式[8]和销轴连接的牵引式[9]2种。牵引式农田平地机平地面积更大，铲车摆向灵活。

对于牵引式农机的导航系统，文献[10-11]通过建立农机具-拖拉机组合系统的动力学模型，提出相应的非线性导航控制器，同时也考虑了侧滑角对导航精度的影响。为了保证控制精度，这些研究在车辆和农机具连接处添加了横向控制器，增加了控制模型的参数。文献[12]对铰接摆杆式大功率拖拉机进行了转向仿真试验。文献[13-16]对铰接式无人驾驶车辆的系统建模、路径追踪算法、导航精度优化和避障进行了深入研究，为牵引式农田平地机自动导航研究提供了思路。农田平地机由拖拉机提供牵引动力，导航过程中通过控制拖拉机前轮转角和后车轮行驶速度的变化引导铲车驶入指定路线，这需要建立不同数学模型来描述平地机的运动状态。同时，在农田环境下，车轮侧滑产生的侧滑角会影响导航控制精度，因此必须考虑侧滑角的影响。针对以上问题，本文提出一种带有侧滑估计的自适应PID导航控制方法，旨在实现基于GNSS的农田平地机的自动导航，提高平地作业的路径跟踪精度。

1 牵引式农田平地机数学模型

1.1 路径追踪状态描述

牵引式农田平地机在平地作业过程中，通过控制拖拉机的行驶状态实现平地铲对规划路径的追踪，车轮与农田表面之间由于摩擦力的影响产生侧滑角。如图1所示，拖拉机与平地铲之间通过销轴进行连接，待追踪路径为曲线C。以后轮轴的中心位置为研究点，得到拖拉机与追踪曲线的位置误差为dTe，平地铲与追踪曲线的位置误差为dFe。拖拉机的前轮转向改变农田平地机的航向，前轮转角为δT，转向过程中产生的侧滑角为β1。拖拉机后轮为驱动轮，行驶速度为VT，路径追踪时产生的侧滑角为β2。行驶过程中，平地铲与拖拉机连接处的夹角为φ，受到牵引力的作用，平地铲的行驶速度为VF，车轮产生的侧滑角为β3。

图1 农田平地机路径追踪状态Fig.1 Path tracking of farmland leveler

1.2 运动学模型

对拖拉机和平地铲简化后的组合模型进行运动学分析，如图2所示。当农田平地机追踪至规划路径C时，拖拉机和平地铲的追踪航向角分别为θTd和θFd，追踪夹角为φd。结合图1可知，追踪点T和F处的曲率半径分别为1/C(sT)和1/C(sF)，农田平地机的路径追踪目的在于实时地调整拖拉机的前轮转角δT和速度VT，使平地铲与曲线C的横向误差dFe趋于0，航向误差θFe趋于0，拖拉机与平地铲的夹角趋于φd。结合文献[17]，拖拉机的追踪误差方程可改进为

(1)

图2 运动学模型Fig.2 Kinematic model

其中

θTe=θTd-θT

式中sT——T点沿曲线C的坐标

θTe——拖拉机航向追踪误差

C(sT)——T点曲率

L1——拖拉机车轮轴距

θT——拖拉机航向角

假设平地铲与拖拉机的连接处存在一个虚拟转向轮，平地铲行驶过程中不断地调整转向角δF，同理可得平地铲的追踪误差方程为

(2)

其中

θFe=θFd-θF

式中sF——F点沿曲线C的坐标

C(sF)——F点曲率

L2——平地铲车轮轴与连接处的距离

δF——平地铲虚拟前轮的期望转角

θF——平地铲航向角

夹角φ与拖拉机航向角θT及平地铲航向角θF的变化有关，由空间位置关系可知

(3)

(4)

式中a1、a2、a3——状态变量对时间的导数

控制变量的线性形式为

(5)

式中m1、m2——控制变量对时间的导数

将式(4)中的a2、a3对曲线坐标a1进行求导，可求得追踪误差(式(2))的链式表达[18-19]

(6)

链式表达式(6)是线性的，可以将控制参数m3表达为

m3=-Kda3-Kθa2(Kd、Kθ∈R+)

(7)

式中Kd——横向误差de的控制系数

Kθ——航向误差θe的控制系数

结合式(6)、(7)，可以得到

a″2+Kda′2+Kθa2=0

(8)

由式(4)、(8)可知，平地铲的横向误差dFe和航向误差θFe都收敛于0。并将式(8)代入式(5)、(6)，可以求得平地铲虚拟转向轮的控制率为

(9)

其中

γ=θFe+β3

η=-KddFe-Kθεtanγ+C(sF)εtan2γ
ε=1-C(sF)dFe

将式(9)和式(3)联立，可得

(10)

由式(10)可知，夹角φ作为路径追踪时关联拖拉机和平地铲的变量，其由平地铲的状态变量(sF，dFe，θFe)和拖拉机的控制变量(VT，δT)共同决定。因此，联立式(10)、(1)可最终求得路径追踪下牵引式农田平地机的运动学模型

(11)

2 导航侧滑估计器

2.1 侧滑角计算

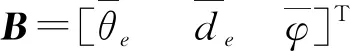
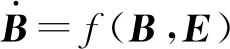
(12)

考虑极限情况下侧滑角减小为0，即农田平地机不发生侧滑，则式(12)可在控制变量(β2，β1，β3)趋于0时进行线性化

(13)

控制变量的预测矩阵D是由函数f(B,E)对控制变量E求偏导后得到

(14)

其中

式(14)中，当横向偏差θTe≠π/2，dFe≠1/C(sF)且λ1+λ2+λ3≠0，则矩阵D可逆。侧滑估计器的目的是使估计变量B与测量变量X之间的误差R为0(R=B-X)，误差的运动学方程可表示为

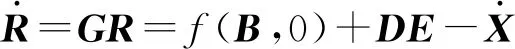
(15)

偏差增益矩阵G为Hurwitz矩阵，定义了所估计的状态变量B向测量变量E的收敛时间[21]。测量变量X的值是等间隔的(取决于采集设备)，因此可得

(16)

其中T为采样周期。最终，通过状态变量和测量变量的不断收敛计算，可求得输入变量E(即农田平地机的侧滑角(β1，β2，β3))

(17)

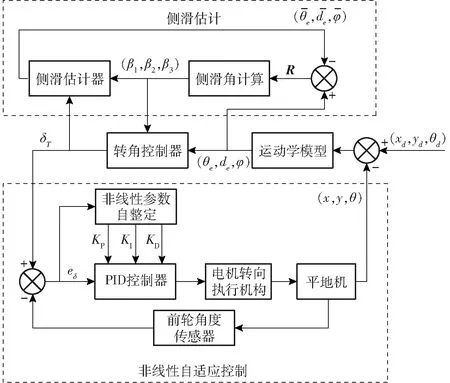
图3 平地机导航的控制结构图Fig.3 Navigation control structure of land leveler

2.2 导航控制率

农田平地机路径追踪时拖拉机的行驶状态(θTe,dTe,VT)和平地铲的行驶状态(θFe,dFe,VF)作为输入变量，是可以通过测量和计算获得的。结合运动学模型，拖拉机的前轮期望转角δT作为平地机导航的控制输入，通过夹角φ建立拖拉机与平地铲的联系。可将运动过程中平地铲相对于拖拉机横摆的曲率看作一阶惯性环节[22]

(18)

将式(18)、(11)联立，可得到农田平地机的前轮期望转角

(19)

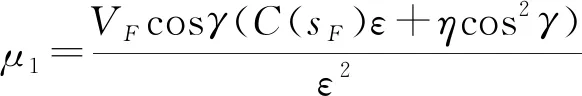
其中采样周期T取决于RTK-GNSS数据接收设备。φd为追踪至期望路径时平地铲与拖拉机之间的理想夹角，φd=θFd-θTd。

3 非线性自适应PID控制

3.1 非线性参数整定

农田平地机路径追踪时，拖拉机的行驶方向由电机转向执行机构带动方向盘实现自动控制。非线性自适应控制结构如图3所示，PID控制器接收到误差输入信号，控制电机转向机构带动方向盘转动，调整拖拉机追踪时的航向。角度传感器实时地测量前轮转角的角度并与转角控制器求得的控制率δT比较，得到误差再输入至PID控制器，形成一个闭环控制系统。

PID比例增益参数KP、积分增益参数KI和微分参数KD的选择会影响控制器适应性和鲁棒性，本文使用一种改进的非线性整定方法[23]，以转角误差eδ(t)为输入量，3个增益参数为输出量，构造非线性整定函数

(20)

式中aP、bP、cP——比例增益范围系数

aI、cI——积分增益范围系数

aD、bD、cD、dD——微分增益范围系数

3.2 自适应控制方法

如式(20)所示，范围系数(正实数)决定着增益的取值区间。当误差eδ(t)→∞时，比例增益系数KP取最大值aP+bP。当eδ(t)=0时，KP取最小值aP。bP为KP的变化区间，调整cP可调整KP的变化速率；积分增益参数KI的取值范围为(0,aI)，当eδ(t)=0时，KI取最大值，cI决定着KI变化速率；对于微分增益，aD为KD的最小值，aD+bD为KD的最大值。当eδ(t)=0时，KD=aD+bD/(1+cD)，调整dD可调整KD的变化速率。

随着转角误差eδ(t)的实时计算，非线性自适应PID控制器的控制输入变量为

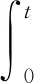
(21)

式中ew(t)——转角误差的变化速率

4 田间试验验证

4.1 试验平台与参数设定

农田平地机以John Deere 5-904型拖拉机为牵引动力，使用北京盛恒天宝公司生产的平地铲，两者通过销轴式半刚性连接，试验现场如图4所示。

图4 农田平地机试验现场Fig.4 Experimental site of land leveler in field

使用上海华测导航公司的GNSS双天线导航定位系统测量农田平地机的运动状态，配置1个中绘i70型基站。移动端的GNSS双天线和接收机有2套：1套GNSS定向、定位天线分别放置于拖拉机前后车轴的中心位置，测量拖拉机运动过程中的位置与航向信息；另1套GNSS定向天线放置于牵引连接处，GNSS定位天线放置于平地铲后轮轴的中心位置，测量平地铲运动过程中的位置与航向信息。2个定位测向接收机的型号都为P3-DT，其平面定位精度为0.8 cm±1 mm，航向测量精度为0.1°。用于接收GNSS天线传输的数据，接收频率设置为5 Hz。采用北京通磁伟业公司生产的WYT-3I3D型无触点角度传感器测量拖拉机的前轮转角，测量精度为0.1°。配合自行设计的步进电机转向平台和导航控制器，实现平地路径的导航追踪控制。

农田平地机的拖拉机前后轴距为2.3 m，拖拉机前轮轴长为1.6 m，拖拉机的后轮轴长为1.7 m，平地铲的宽度为2.5 m，平地铲前后轴距为2.7 m。通过前期的Matlab/Simulink仿真平台的调试，结合平地导航所使用的步进电机转向控制系统的特性[24-25]，本文的电机导航系统响应追踪达到稳定时，非线性整定函数的比例增益范围系数aP、bP、cP分别为1.2、2.5、0.2；积分增益范围系数aI、cI分别为2、0.5；微分增益范围系数aD、bD、cD、dD分别为0.5、1.5、4.5、0.3。再由手工试凑法，得出横向偏差系数Kd为1，航向偏差系数Kθ为2时导航控制系统的振荡最小。同时可得偏差增益矩阵为

(22)

4.2 田间平地机的导航试验

试验地点位于中国农业大学上庄实验站，选取1块收获玉米后旋耕过的农田，设定的追踪路径由3条直线与2条曲线组成。分别进行3次路径追踪试验：试验1导航控制方法带有侧滑估计器，但PID参数固定；试验2导航控制方法既有侧滑估计器，又进行非线性参数整定；试验3导航控制方法无侧滑估计器，且PID参数固定。

图5 平地机路径追踪试验结果Fig.5 Path tracking experiments results for farmland leveler

农田平地机3次试验的路径追踪效果如图5所示，为了符合农田平整时的作业条件，农田平地机的追踪起始点距离设定路线大于1 m，拖拉机的行驶速度控制为1.05 m/s。分析图6a的路径追踪偏差变化，可知拖拉机与平地铲的路径追踪时间随着起始距离的变大而增加。当追踪路线由直线至曲线或曲线至直线过渡时，拖拉机实时地调整自身位置，牵引平地铲向规划路径行驶。使平地铲路径过渡时的偏差峰值小于拖拉机的峰值，平地铲的路径追踪误差快速下降。

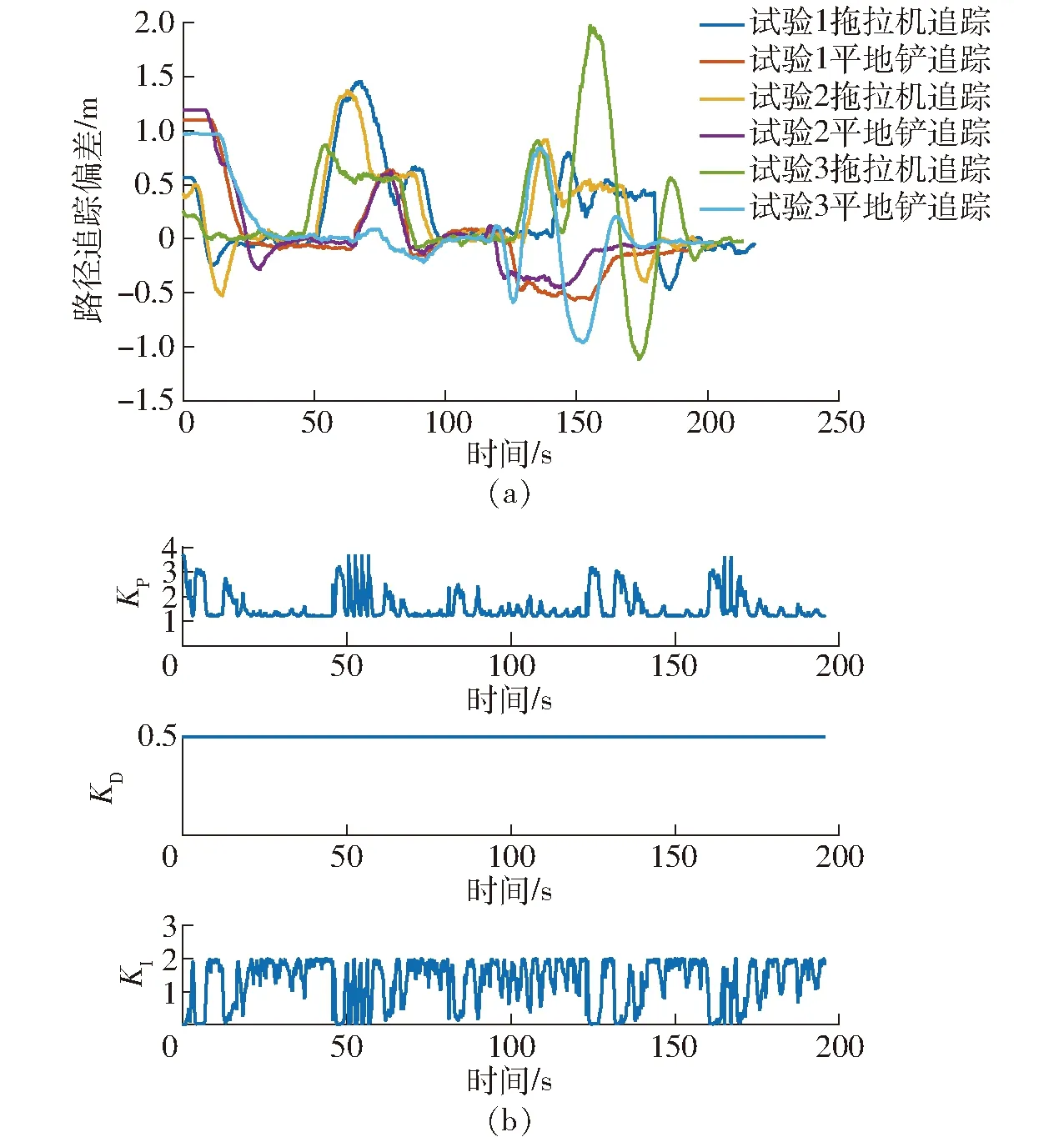
图6 平地机路径追踪偏差与参数变化Fig.6 Changes of path tracking deviation and gain parameters for farmland leveler

农田路径追踪偏差结果如表1所示，可知试验3在不考虑侧滑角和参数自适应控制的情况下，拖拉机最大偏差达1.976 8 m，标准偏差为0.448 2 m，平地铲标准偏差为0.326 4 m。这是由于拖拉机在追踪路线变换时发生侧滑，为牵引平地铲驶向规划路线不断调整自身航向，导致追踪偏差变大。试验1使用了本文设计的侧滑估计器，农田平地机在对第2条曲线至第3条直线路径进行追踪时，侧滑现象的影响减弱。拖拉机的标准偏差减小至0.358 1 m，

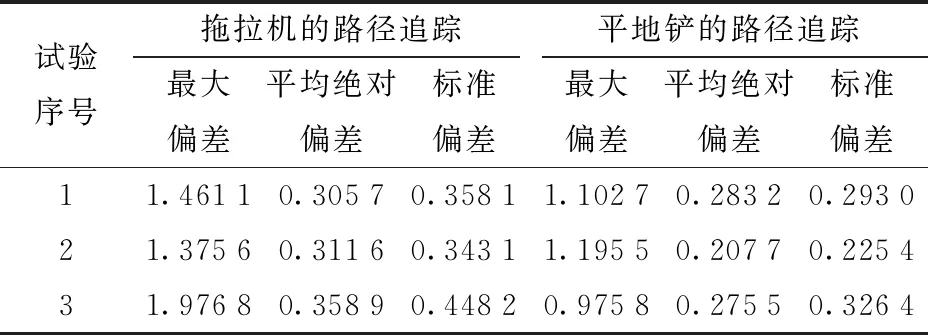
表1 农田路径追踪偏差结果Tab.1 Deviation results of farmland path tracking m

平地铲路径追踪的标准偏差减小至0.293 0 m。试验2的路径追踪效果最为显著，拖拉机和平地铲路径追踪的标准偏差分别为0.343 1 m和0.225 4 m，相比于试验3，试验2中平地铲路径追踪的平均绝对偏差减小了6.78 cm，标准偏差减小了10.1 cm。试验2中增益参数KP、KI、KD的变化如图6b所示，表明本文提出的非线性自适应控制方法可以实时地根据输入转角误差，调整PID的3个增益数值。

路径追踪时的角度变化如图7所示，结合图7a，在试验2的路径追踪过程中，导航控制器控制转向执行机构。使前轮转角快速地追踪至转角控制器计算的理论转角，表明本文所使用的非线性自适应控制方法可以很好地调整增益系数，增强了PID控制器对农田平地机导航控制系统的适应性和鲁棒性。同时从图7b可以看出，侧滑角峰值变化的时间区间与路径追踪误差峰值变化的时间基本一致。说明农田平地机在路径追踪的过程中，当追踪路径由直线向曲线路径变化时，平地机整体的航向角出现较大变化，此时侧滑的影响最为严重，证明本文提出的侧滑估计方法可以合理有效地预测平地机在田间路径追踪时的侧滑角。

图7 试验2路径追踪时的角度变化曲线Fig.7 Angles changes during path tracking in experiment 2

5 结论

(1)建立了牵引式农田平地机的运动学模型，以横向偏差、航向偏差、车辆机具之间的夹角为输入量，提出了一种侧滑估计器，实时计算农田平地机进行路径追踪时产生的侧滑角，提高了导航控制率的计算精度。

(2)采用改进的非线性参数整定自适应PID控制方法，根据转角输入误差在线调整PID控制器的增益参数，使导航控制系统的适应能力得到提高。

(3)田间导航试验表明，相比于无侧滑估计与参数自适应的导航控制，带侧滑估计的自适应控制方法可以削弱侧滑对农田平地机路径跟踪的影响，增强了导航控制器对农田平地机系统的适应性和鲁棒性。当行驶速度为1.05 m/s时，平地铲路径追踪的平均绝对偏差减小了6.78 cm，标准偏差减小了10.1 cm。该方法有效解决了农田平地机路径追踪时平地铲对规划路径的准确跟踪问题，适用于无人驾驶的农田平整作业。