激活思维，提升能力——一节数学课的教学改进与思考

（桐乡市洲泉中学，浙江 嘉兴 315000）

学生在数学学习的过程中经常会出现各种思维障碍，其原因是多方面的，但主要的原因是数学课堂中大量存在着缺少学生参与数学思维活动的现象，往往略去了知识的探究过程，取而代之的是教师一言堂和机械的训练。尤其是优等生缺乏对知识的“火热”思考和主动建构，因而思维能力的提升就无从谈起。《新课标》指出，数学教育既要使学生掌握现代生活和学习中所需要的数学知识和技能，更要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用。数学教学活动，特别是课堂教学应激发学生兴趣，调动学生积极性，引发学生的数学思考，要注重培养学生良好的数学学习习惯，使学生掌握恰当的数学学习方法。为此，我校对九年级学生实施分层教学，给优等生创造了一个良好的课堂学习氛围，同时也为数学教师们提供了分层教学的环境。

一、留足时间，打开思维通道

陶行知认为，在初中数学教学中，教师要留给学生动脑的机会，让学生有较充分的思考时间和空间，发表自己的见解，这样才有助于培养学生的探究精神，训练学生的创新思维能力。优等生除了掌握基本的知识和概念以外，更应该注重能力的培养，课堂是培养优等生思维能力的最佳基地。

下面以《浙教版九下数学§2.1 直线与圆的位置关系（1）》中的例5、例6 为例，通过两种教学方式的比较，来验证：在数学课堂的教学中，把时间还给学生，更有助于激发学生的思维，打开学生的思维通道。

例5 木工师傅可以用角尺测量并计算圆的半径.如图1，用角尺的较短边紧靠⊙O于点A，并使较长边与⊙O相切于点C.记角尺的直角顶点为B，量得AB=8cm，BC=16cm。求⊙O 的半径.

（一）克扣时间，效果不佳

在之前的教学中，笔者总是为了能够顺利地完成教学任务，

克扣学生的思考时间，便迫不及待地在课件中呈现早已设置好的几个小问题。如例题5 会设置以下几个问题：

（1）遇到切点，我们往往会将切点与谁连结？（连结圆心和切点）；

（2）求半径长度，可构造哪一种图形？

（3）当图形中出现多个直角时，可构造哪一种特殊四边形？

通过这种逐步引导的方式来帮助学生形成解题思路，最终通过师生的短暂互动得到下面“方法二”的解题过程，以致优等生朝着教师课前设置好的思路走下去。这样虽能完成教学进度，但学生没有了自己的思考时间和空间，久而久之会对老师产生依赖心理，导致学生在做作业时，一旦没有教师在旁指点一二，便不能够很好地完成有难度的习题。

（二）放手一搏，喜出望外

暂停讲解，先给学生足够时间思考，接着倾听他们的思考过程和结果，再进行点评和引导。

经过5 分钟的思考，学生首先提供的是下面的方法一

（我很茫然，辅助线添加得也太多了一点，但我还是打算耐心地听一听）

师：生3很棒，大家的想法也很默契！那么同学们还有其他的解决方法吗？

（停顿了一会儿后，见学生们没有思绪，稍作提示。）

师：同学们的刚才的解决方法使通过相似三角形的性质求出半径的，那求线段的长度除了这个方法外，还有哪一种更常用的方法呢？……

生4：勾股定理

师：很好，那如何来构造这个直角三角形呢？请同学们结合题中的条件再次思考。最后在大家的相互协作下，完成了下面的“方法二”。

通过课后反馈，学生首先想到的是用勾股定理求出线段AC 的长；接着根据AC 在圆中扮演“弦”的角色，又因为所求的是圆的“半径”，自然而然想到了垂径定理，还有部分学生运用的是等腰三角形三线合一性质，故而如此添加辅助线；再根据多个直角（∠B，∠OCB），并结合图形，又进一步联想到了K 字形相似，从而解决了问题（即方法一）。可见学生的想法自然，清晰到位，并且计算简单，并不逊色于书本提供的方法。若教师一味地牵着学生的鼻子走，不但不利于学生智力的开发，还会大大打击学生们的学习自主性。接着以相同的课堂教学方式，分析并完成了例6 的教学。

例6 已知如图,4，直线AB 与⊙O 相切于点C，AO 交⊙O 于点D，连结OC，CD.求证：（注：几何知识中倍角关系的证明是一个重要的知识点，学生急需掌握相应的解题思路和方法。）

课堂上给优等生充足的时间和空间，有利于激发他们去发现和去创造的强烈欲望，加深他们对所学知识的深刻理解，训练他们对数学思想和数学方法的娴熟运用，锻炼他们思维的广阔性和深刻性、灵活性和独创性，从而培养他们的思维品质。

二、及时总结，把握思维方向

及时总结可以帮助优等生理清所学知识的层次结构，掌握其外在的形式和内在联系，形成知识系列及一定的结构框架。通过对所解问题的及时总结，可以帮助优等生掌握解题的方法和经验，从而提高他们的思维能力。

课堂教学中，当学生被激发出多种思维解决同一问题以后，一定要采取及时总结的措施，帮助学生一起整理解决问题的思路和方法，让他们的能力更加精进。经过长期的训练，会让优等生养成及时总结的良好习惯，有助于他们在做习题的过程中把握思维的方向，有效地解决问题。

对于方法的总结要简洁、准确，把握解题的中心，因此我采用“希沃尔技术”呈现解题方法的详细过程，便于优等生回忆解题过程；再借助“学科思维导图”整理各种方法的解题思路，便于学生进行比较和总结，让学生能够根据所求问题，掌握解题的技巧，积累解题的经验。

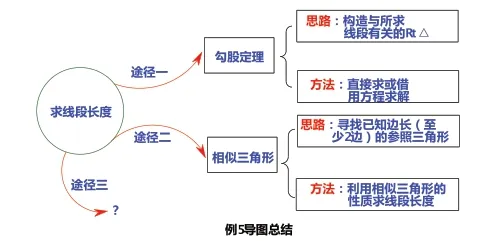
（一）总结例5，把握求线段长度的思维方向

师：请同学们根据上述两个方法的解题思路，请思考一个问题：当我们再次遇到有关求线段长度的问题时，可从哪些方向入手去寻找问题所需的条件，然后根据题中各个已知条件展开合情推理，找到问题解决的思路和方法呢？

结合刚刚的思路整理，采用“逆推”的方式，借助思维导图，便能简洁、清晰地展示求线段长度的基本思路和方向。通过这样的方式进行整理和总结，让学生掌握及时总结的方法。

任务：请同学们在课后翻阅做过的类似习题，找找还有没有其他方法可用来求线段的长度，并进一步完善“求线段长度”的思维导图。通过对方法的整理和归类，有助于优等生今后更加有效地落实课堂和课后作业，帮助他们减轻学业负担，从而能腾出更多的时间去思考、去钻研，让他们的能力得到进一步的提升。

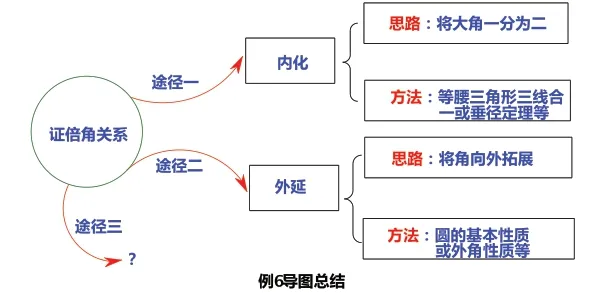
（二）总结例6，把握证倍角关系的思维方向

证明倍角关系是初中数学几何中的一块重要内容，因此把握思维方向，掌握方法很重要，那么证明倍角关系又有哪些思维方向呢？先结合例6 的两种方法，进行思路整理。再让学生根据上述两幅思维导读，并结合例5 思维导图的方法，完成右图这一幅有关倍角关系证明的导图。

通过对证倍角关系思维和方法的总结，有助于优等生加强几何问题的证明和逻辑思维的培养。

首先根据解题方法缕清思路，再用逆向思维总结方法，是初中数学常用的学习方法。要让学生具备这样的能力，及时总结必不可少。一旦养成良好的总结习惯，可为优等生今后的数学学习和研究、能力的锻炼打下坚实的数学基础。

三、延伸拓展，提升思维能力

知识的延伸拓展和方法的应用，可以有效地促进知识的迁移，同时能提高优等生的学习积极性，培养参与意识；促进知识网络的形成，架构思维的桥梁，提升优等生的思维能力。

为了让学生感受到总结的作用，同时检测刚才的教学是否有效，“延伸拓展”这一环节便可起到一举两得之功效。

（一）精选习题

（2）如图8，当当∠A ＜90°时，请判断第（1）小题的结论是否仍成立，并说明理由。

让学生通过对这个习题的练习，了解在初中数学几何问题的学习中，可通过倍角关系去证明线段之间的关系，从而掌握知识点之间是相互联系，不可分割的，它们能组成一个强大的知识网络。同时让优等生了解到证线段的关系不光可以从线段本身入手，还可以从角之间的关系、边角的关系去落实，达到升华思维之目的。

（二）解决问题

优等生有了思考的方向，更应该放手，将课堂再次还给他们，由他们去创造和发挥。先单独思考，再合作讨论，最后由他们通过自己的智慧，去收获喜悦。

（三）课后作业

请同学们于课后完成下面习题：

（1）求抛物线的表达式；

（2）连结OB，点P 为x轴下方抛物线上一动点，过点P 作OB 的平行线交直线AB 于点Q，当S△POQ：S△BOQ=1：2 时，求出点P 的坐标.（坐标平面内两点M之间的距离

布置这个问题的目的是让学生通过对第三小题的解答，总结出：我们可以通过作角平分线证倍角关系，那么证倍长关系，可以通过取线段中点，通过类比的方式，找到思维的突破口，把握思维的方向，促成思维能力的提高。

总之，对于初中数学优等生的教学，除了教会他们掌握基本的知识和概念以外，更应注重他们能力的培养。因为只有提高优等生的思维能力，让他们学会分析问题、解决问题、总结方法、积累经验并学会运用，才能从根本上解决他们的学业负担，减轻他们的心理压力，真正达到“学为中心”、“轻负高效”之目的。