冻结立井爆破近区井壁振动信号基线漂移校正和消噪方法*

付晓强，杨仁树，刘纪峰，张会芝，张仁巍

（1. 三明学院建筑工程学院，福建 三明 365004；2. 三明学院工程材料与结构加固福建省高等学校重点实验室，福建 三明 365004；3. 北京科技大学土木与资源工程学院，北京 100083）

冻结井筒采用钻爆法施工时，新浇混凝土强度较低，复杂受力下局部极易产生应力集中，形成不同方向、不同尺度的裂隙和缺陷，这些累积损伤会造成混凝土井壁强度降低、各项物理力学参数与设计初值相比发生较大差异等问题，最终造成井壁承载能力下降，致使井壁位移量过大，易诱发冻结壁破坏、冻结管断裂等安全事故[1-3]。开展井壁振动监测是评估爆破条件下井壁振动响应特征的有效手段之一。振动测试过程中，由于测试环境影响、仪器系统自身原因及监测方案存在缺陷，监测振动波形会局部存在偏离基线中心的现象，即信号基线漂零。尤其在距离爆心位置相对较近的爆破近区，采集信号基线偏离问题更加显著。根据经典的萨道夫斯基公式，对于同一类型爆破工程而言，在理想测试环境下，若振速幅值相当，则最大段药量越大，信号中存在趋势项的概率也相对较大，相应的“近区”的范围也越大。更进一步地，若信号同时存在高频噪声，则两者的不利因素相互叠加，若不采用有效的方法消除上述影响，则整个信号会受到污染，严重影响信号特征的准确提取。因此，在信号预处理时必须予以基线校正和噪声消除，避免对信号相关特征分析的干扰。

针对非线性振动信号存在干扰成分的问题，相关学者开展了具体的研究，如：张军等[4]针对车载武器振动信号中趋势项消除的难题，根据信号自身特点，研究了基于经验模态分解（empirical mode decomposition, EMD）的信号趋势项提取和判别方法；张景元等[5]通过对导弹自动驾驶仪振动信号进行分析，提出了基于形态学的解决振动信号中基线漂移问题的滤波方法，有效抑制了信号中的基线成分；刘艳丽等[6]基于形态学滤波方法，对脉搏波信号的基线漂移进行了校正，为准确诊断病人的亚健康状态提供了技术手段；谢芳娟等[7]为了消除基线漂移及噪声对信号分析的干扰，提出了基于空域追踪的修正算法，并通过实例对算法的可靠性进行了验证。

对爆破振动信号干扰性处理的研究，主要集中在趋势项的修正和滤波去噪方面，如：张胜等[8]通过对实测爆破信号进行分析，提出了以时域积分后的振速信号构造模式自适应小波基的方法，并成功地去除了爆破信号中的趋势项；韩亮等[9]利用集合经验模态分解（ensemble empirical mode decomposition,EEMD）及小波相关方法，提出了以固有模态函数频带分布为指标进行人工判别趋势项的去除方法，以及基于自相关分析识别噪声特征的小波阈值去噪方法，并应用该方法进行露天深孔台阶爆破信号趋势项去除，收到了良好的效果；王志亮等[10]采用集合经验模态分解与高低频处理相结合的方法，对花岗岩爆破振动加速度信号中的漂零信号进行了修正，并对该算法的局限性进行了进一步的讨论。

爆破振动信号存在基线漂零和噪声的主要因素包括仪器自身原因、测试环境（温度变化、飞石及环境干扰）及测试方法等，其中仪器自身原因、测试环境属于测试中的不可控因素，而测试方法的优化能很大程度上降低甚至避免上述现象对信号波形的干扰。本文针对冻结立井的井壁振动测试，提出传感器井壁预埋振动监测方法，以实现冻结立井爆破近区井壁振动信号的实时准确监测；对爆破近区井壁振动信号中存在的明显基线漂零现象进行校正，并采用最优化去噪方法对校正信号进行消噪分析；通过几种去噪方法评价指标对比和交互小波变换相关性分析，检验基线修正和消噪效果，以期为爆破振动等非线性信号基线漂零校正和噪声消除提供新思路。

1 算法原理

1.1 互补总体经验模态分解算法

在经典的希尔伯特-黄变换基础上，Yeh 等[11]提出互补总体经验模态分解（complementary ensemble empirical mode decomposition, CEEMD）方法。该方法是在传统EMD 分析的基础上改进的一种噪声自适应的完备算法[12]，利用噪声进行辅助分析，可有效解决EMD、EEMD 算法中的模态混叠问题。该方法的核心在于将原始信号中添加一对相反的白噪声信号，对生成的信号分别进行EMD 分解，将分解得到的固有模态函数（intrinsic mode function, IMF）进行优选重组，以得到最终信号。该算法在保证分解效果的同时，有效抑制了由白噪声引起的重构误差。

该算法步骤为[13]：

(1) 向原始爆破信号S 中加入正、负成对的辅助白噪声，从而生成两个信号S+和S−：

式中：N 为辅助噪声；

(2) 对S+和S−做EMD 分解，分别得到两组IMF 函数，记为Si+和Si−：

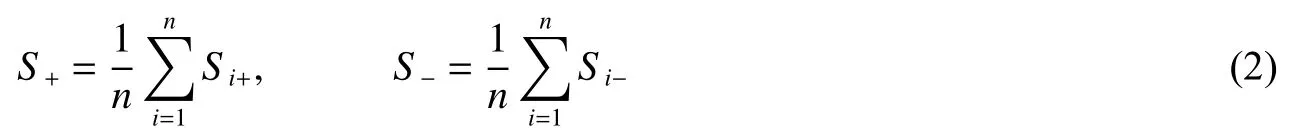
(3) 通过将两组分量组合便得到信号S 分解形式为：

式中：Si为信号S 的模态函数分量IMF i，R 为残余项。

1.2 稀疏化基线估计消噪算法

稀疏化基线估计消噪（baseline estimation and de-noising with sparsity, BEADS）算法具体过程如下。

对于任意给定的稀疏化信号s，若其中含有n 点随机基线成分，则该信号可视为特征波形信号和缓变基线漂移信号的叠加[14]，即：

式中：x 为多峰值且稀疏可导的信号矩阵；f 为信号中含有的基线成分，为低通信号。可将观察到的受基线漂移和噪声影响的信号进一步分解为：

式中：w 是方差为 σ2的平稳高斯白噪声，信号分析最终目的是剔除信号中含有的基线成分并保留含有峰值点的特征信号。若假定信号不存在峰值，则基线可通过低通滤波器从受噪声污染的观察信号中近似恢复，即：

1.3 交叉小波变换

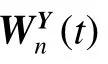
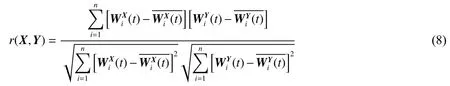
式中：上标的“—”表示对所有分量求平均值。

这里，选取Morlet 小波作为小波基函数，以反映两个爆破振动信号经小波变换后在时频域上相关性振荡的时频结构特征。

1.4 相关性检验

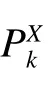
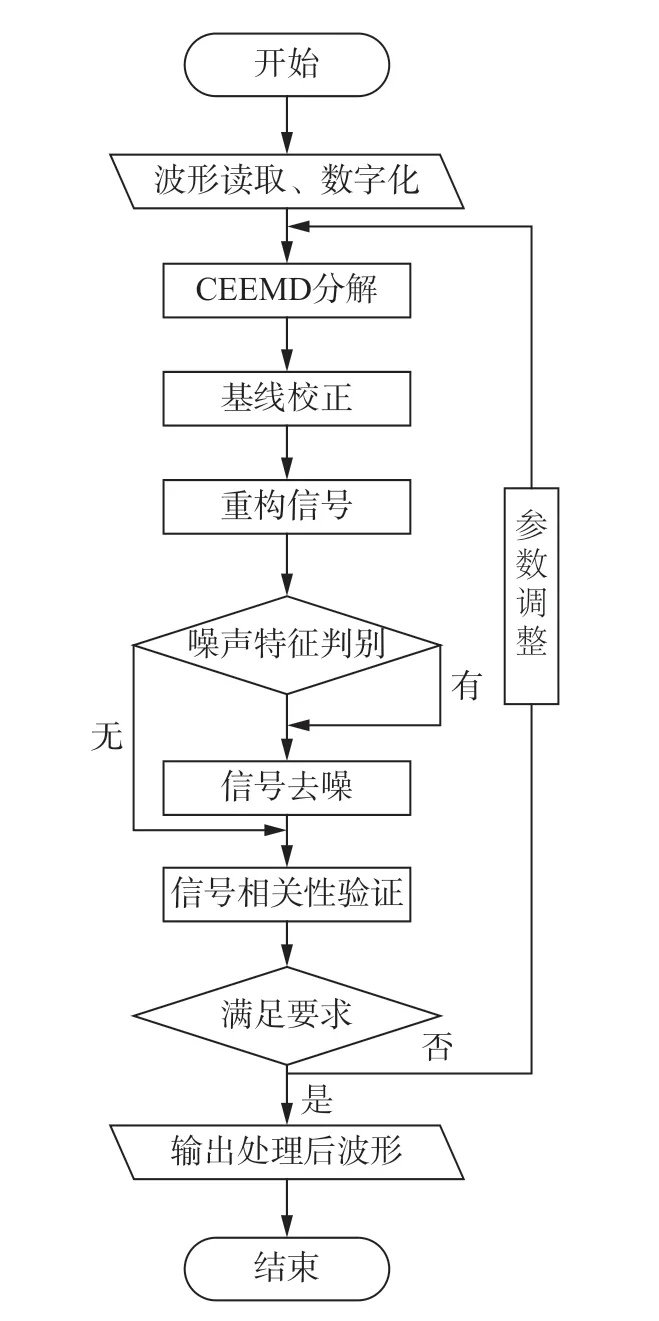
图1 基线校正及消噪流程Fig.1 Baseline correction and noise reduction process

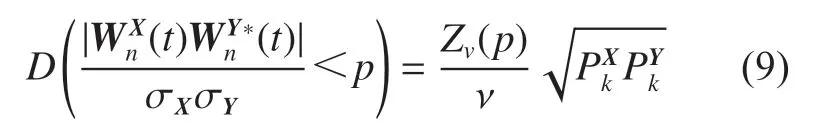
式中：|W|表示矩阵W 的行列式；σX、σY分别为时间序列的标准差；Zv(p)是与概率p 有关的置信度；对于实小波， v=1 ，对于复小波，v =2 。在显著性水平α=0.05 条件下，Z1(95%)=2.182，Z2(9 5%)=3.9 9 9，则认为通过显著性水平α=0.05 条件下红噪声标准谱的检验，即两者之间显著相关。

1.5 基线校正和噪声消除流程

根据上述算法理论，整理得到冻结立井爆破近区井壁振动信号基线校正和噪声消除方法，利用matlab 软件编制程序，可实现信号的批量化处理，具体如图1 所示。

2 实例分析

2.1 信号获取

与巷道有所不同，冻结立井施工作业空间狭小，井下环境恶劣，尤其是冻结低温的条件和高强混凝土初凝期的水化热现象会对测振仪器的性能和准确性产生负面影响。上述因素对立井爆破振动的现场监测带来很大挑战。针对测试过程中存在的问题，本次现场试验对传统测试方法进行改进：采用传感器预埋安装（绑扎固定在井壁钢筋交叉点处）、大容量专用防爆电源长期供电、专用隔爆保温防护箱等技术措施，集成开发了冻结立井爆破振动监测系统，减少电线敷设、检查和回收等大量工作，避免施工对振动测试的干扰，以实现冻结立井井壁爆破振动信号的长期、稳定和实时监测。具体布置方案如图2 所示。

图2 传感器井壁预埋法Fig.2 Pre-embedding method of vibration instrument

采用井壁预埋法在兖矿集团万福煤矿对主立井爆破掘进过程中井壁振动进行了有效监测。该井筒净直径为5.5 m，深度886 m，冻结深度894 m，井筒施工需穿过753 m 的表土层，是地质条件极为特殊的井筒，表土层厚度目前是世界第一。测试段为双层井壁结构，钢纤维高强混凝土井壁强度为CF90，单侧厚度1.9 m，测振传感器固定在内层井壁。爆破采用直眼掏槽形式，1～5 段毫秒电雷管，掏槽眼深度4.2 m，其余炮眼深度4 m，单循环炮眼总数135 个，总装药量339.9 kg，炮眼具体布置如图3 所示。

通过对不同测距处的信号对比发现，在爆破近区处采集到的井壁振动信号基线漂零现象显著，如距离立井爆破掌子面3 m 处，采集到的井壁垂向振动信号时程曲线如图4 所示。该振动信号波峰值为6.35 cm/s，波谷值为−4.78 cm/s，峰峰值为11.13 cm/s。从图中可知：监测信号中包含一定的杂波成分，并且信号波形存在明显的基线漂零（“甩尾”）现象。信号在时间轴上0.1 s 内监测波形稳定，随后存在严重的基线偏离问题，信号历时波形在时间轴0.3 s 后逐渐回归基线中心并最终趋于稳定。由于爆破网络中周边眼所用的MS5 段雷管标定延期时间为(110±15) ms，超出了稳定波形所在时间轴范围。因此，基线漂零会对爆破信号分析产生不利影响。

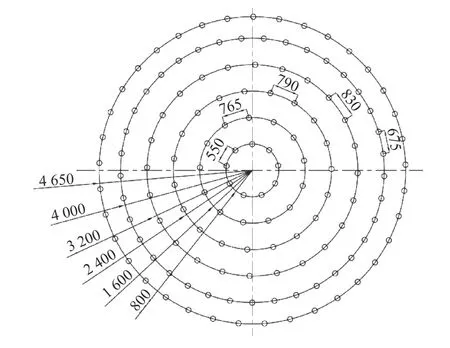
图3 炮眼布置（单位：mm）Fig.3 Borehole layout (unit: mm)

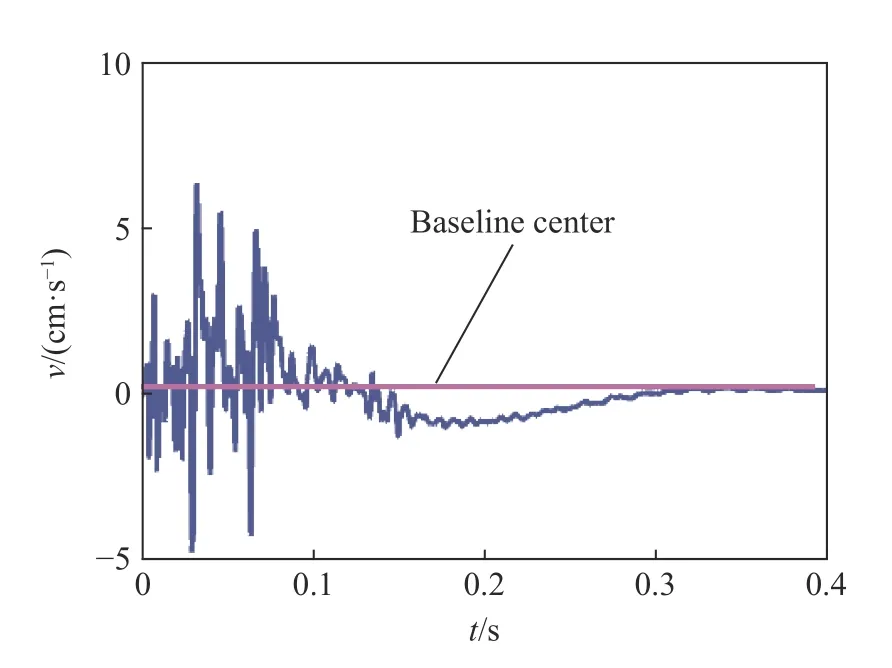
图4 爆破近区井壁振动信号Fig.4 Vibration signal of shaft lining near blasting area

2.2 信号基线漂零校正

2.2.1 CEEMD 分解

由于信号分析过程中的不同处理阶段的误差会逐步累积，所以分析过程中的各个步骤分析方法均需优选，确定最适合信号特点的分析方法，从而最大程度保留和还原信号的固有特征属性。本次分析设置初始白噪声标准差为0.2，筛分次数为5，最大筛分迭代次数为100。经过5 次筛分，各IMF 分量迭代次数分布情况如图5所示。

图5 表明，信号的IMF 分量越复杂，迭代次数也越多，包含的信息越丰富，对原始信号信息的继承度也越高。最终，信号经CEEMD 运算被分解为11 个IMF 分量和1 个残余项R，具体如图6 所示。

本次CEEMD 算法中，按照信号的复杂程度和频率高低将其分解为若干个独立分量，分解得到的IMF1～IMF7 分量端点振荡效应和模态混叠已基本消除，但具有典型的含噪信号特点，即多峰值、多频带随机特征。而剩余的其余低频分量在波形初始零时刻（或波形尾部截止时刻），均较基线中心位置出现显著的偏离（椭圆线所标记处）。由于信号中存在缓变的基线趋势项，需要建立低通滤波器予以校正和消除。为了客观评价各IMF 分量与原信号的相关度，这里将趋势项R 也作为一个分量（IMF12），利用互相关函数确定其对应的相关度值，见表1。

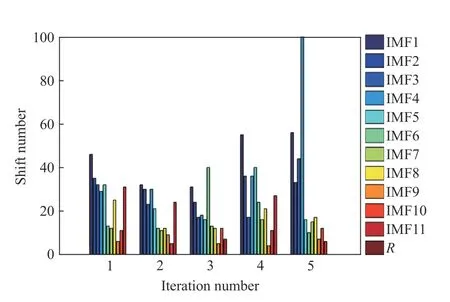
图5 各IMF 分量筛分迭代次数关系Fig.5 The relationship of iterations number and shift number

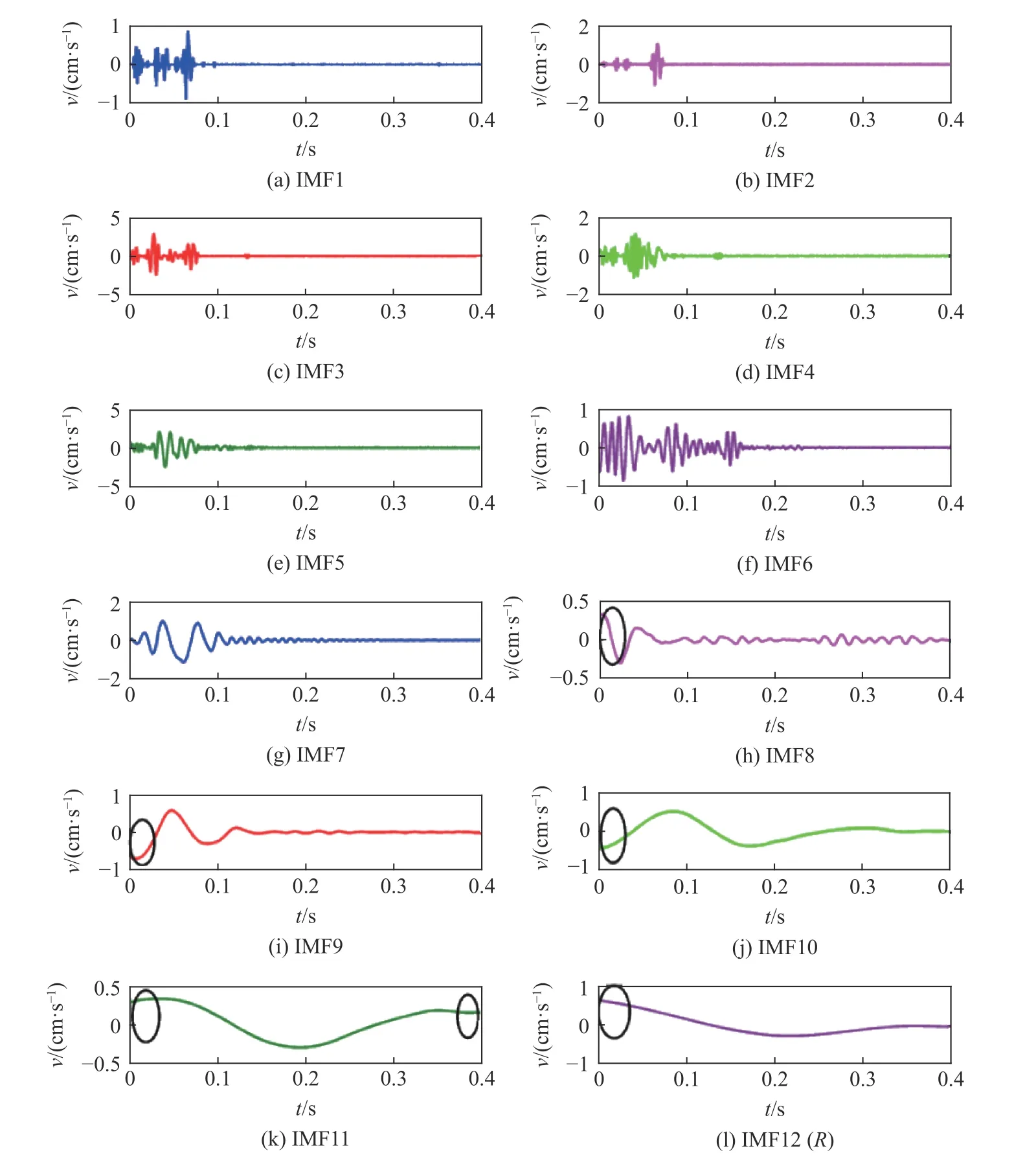
图6 信号CEEMD 分解各分量及残余项RFig.6 Component of CEEMD decomposition and residual signal

表1 模态分量与原信号相关度Table 1 Correlation between components and original signals

从表1 中可知：IMF1～IMF5 分量的相关性系数远大于IMF6～IMF9 分量，同时应注意到IMF10、IMF11 分量及残余项R（趋势项）与原信号的相关性也较大，如IMF11 分量值甚至超过IMF1～IMF4 分量，说明传统的CEEMD 分析中直接将残余项及相关分量舍弃的信号重构方法，会导致信号有效成分的严重丢失。从图6 中也可看出趋势项幅值较大，因此在分析过程中不能完全舍弃，应采用合理的算法将其中包含的有效信息进行提取，避免导致信号成分的缺失。

2.2.2 信号基线校正

对于给定的基线偏移和含噪信号y，可将其建模为m 个基本波形（或称为信号原子）的线性组合，从而得到其稀疏化的表达形式：

式中：x 为待提取信号y 的稀疏化形式；w 为信号中包含的标准差σ＞0 的高斯白噪声；Φ 为n×m 的过完备稀疏表示系数矩阵；xj(j=1, 2, 3,···, m)为y 在字典Φ=[φ1,φ2,···,φm]下的稀疏表示系数；信号原子φj为Φ 的列向量，一般将其归一化到单位 ℓ2范数，即：

式中：φij为Φ 的分量，i=1, 2, 3,···, n。

根据式(10)，字典Φ 下稀疏化信号y 可以通过信号原子簇φj中的部分原子的叠加而准确描述。

在分析过程中，为了降低基线校正过程对信号分量幅值的影响，引入决定该过程中信号稀疏化程度的正则化系数 λ 和具有非对称补偿罚值功能的对称罚函数 φ:R →R ，则问题转化为下述优化问题，也称为基追踪去噪（basic pursuit de-noising, BPD）过程[14]：

由于基线成分主要位于信号低频分量中，分析时设置信号截止频率fc为0.002 Hz，滤波器阶数d 取为0～2，罚函数非对称性参数r 取为6。正则化参数幅值为0.8，不同阶正则化参数 λ0～λ2分别为：0.4、3.2 和4。

根据上述理论，对图中分解得到的12 个固有模态分量分别进行BEADS 算法处理。限于篇幅，这里仅给出IMF3、IMF8～IMF11 和残余分量R 共6 个分量基线成分和校正后的信号曲线，见图7。图7 表明，BEADS 算法可准确识别各模态分量信号中包含的缓变的低通基线杂波成分，且信号不存在明显的畸变和局部细节特征缺失。在相对高频段分量（IMF1～IMF4）中的基线成分主要位于主振时刻内（小于0.1 s）且幅值均较小；相对中频段分量（IMF5～IMF9）中的基线成分主要位于主振时刻内，幅值与高频段相比较大；而相对低频段分量（IMF10～IMF11 及R）中含有的基线成分幅值较大且持续时间较长，为信号中趋势项的主要来源。

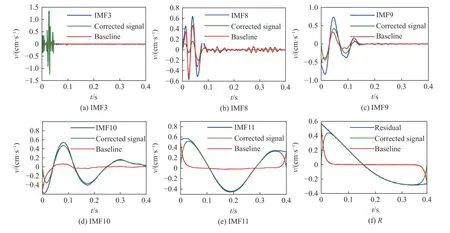
图7 模态分量处理结果Fig.7 Results of baseline correction processing

图8 为各模态分量分离出的其中含有的基线成分。说明基线成分存在并遍历CEEMD 分解的整个过程。低频分量中基线偏移幅值比高频分量相对较大，具备典型的低通特性，这与图7 的分析结果一致。图9 给出了各分量校正过程中罚函数值与迭代次数的历史关系曲线。从图9 可以看出，在迭代有限次数（小于20 次）罚函数值便趋于收敛，这验证了算法运算速度和特征提取的有效性。

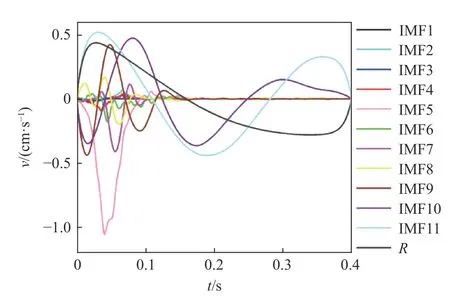
图8 各分量基线成分Fig.8 Baseline of each component

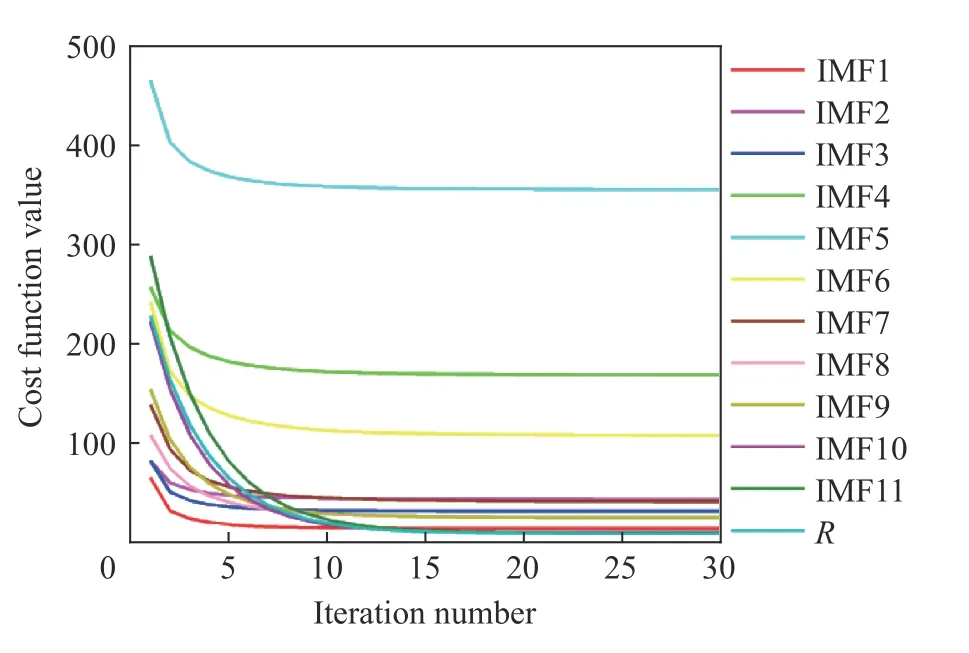
图9 罚函数值与迭代次数关系Fig.9 Relation of cost function and the iteration number

采用BEADS 算法进行基线校正后的波形时程曲线如图10 所示。参考相关文献并结合相关性分析结果，剔除信号趋势项R（IMF12 分量）并将相关性系数较大的IMF 1～IMF 5、IMF 10～IMF 11 分量重新组合便得到了CEEMD 方法处理后的重构信号，如图11 所示。

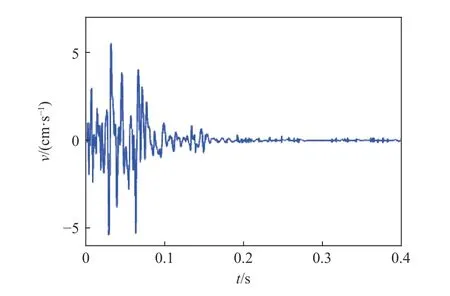
图10 基线校正后信号Fig.10 Baseline corrected signal

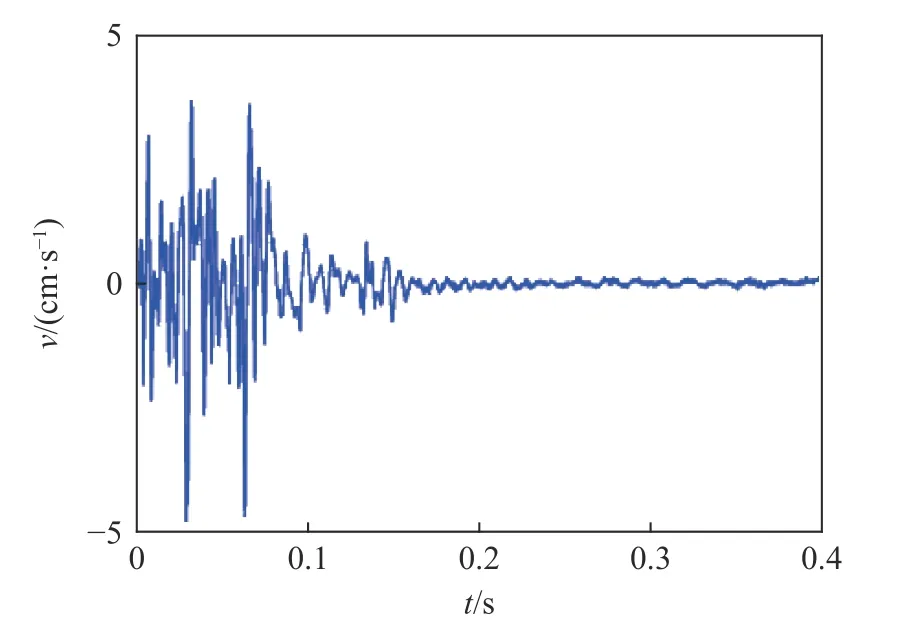
图11 CEEMD 重构信号Fig.11 Reconstructed signals of CEEMD

对比图10 和图11 可知：剔除残余项及相关低频分量的信号处理方法，使得重组信号幅值降低，波峰值和波谷值分别为3.68、4.35 cm/s，峰峰值为8.01 cm/s，与原信号幅值出现了很大偏差；同时，高频分量干扰噪声的残留及低频有效成分的缺失现象均较为严重，在实际分析中需要进行相应的处理，这增加了分析难度和复杂性。

2.3 信号消噪

BEADS 算法对信号中的基线漂零和低频噪声处理效果较好，但无法完美地滤除信号中的高频噪声。通常认为信号中包含的高频噪声满足关于时间的泊松分布，高频噪声的幅值与信号的强度（峰值+基线）的平方根成正比。为了寻求最优信号消噪效果，本文分别采用形态学消噪（morphological de-noising, MD）、奇异值消噪（singular value de-noising, SVD）、小波熵消噪（wavelet entropy denoising, WED）和隐马尔可夫模型消噪（hidden Markov models de-noising, HMMD）四种方法对图中的基线校正信号进行消噪处理，以上消噪方法的相关理论见文献[16-20]。MD 方法充分利用信号波形的形态特征实现其消噪过程，具有运算速度快，自适应强的特点；SVD 方法通过构建信号奇异值矩阵，利用信号和噪声的能量可分性，在信号重构过程中将光滑信号所产生的奇异值保留、噪声信号奇异值置零，从而实现消噪信号特征的最优化估计；WED 方法中，选取“db8”小波基函数，进行3 层分解，计算得到各层的熵值，最后利用wdencmp 函数实现对信号噪声的压制；HMMD 方法是基于统计数据而提出的新的信号处理方法，该方法不受人为门限设置的影响，已在信号处理相关领域得到成功应用。为了获得最佳分析信号，本文采用信噪比（signal to noise rate, SNR）、均方根误差（root mean square error, RMSE）、相关性系数（coefficient of correlation, CC）和峰值误差（peak error, PE）四个指标来综合评价不同去噪方法的消噪效果。不同方法消噪效果如表2 所示。

表2 不同方法消噪性能指标Table 2 Indexes of noise reduction performance

从表2 中各项指标的对比可知：MD 方法避免了小波阈值选取及信号重构，具有自适应特点，但迭代次数选择不合理易导致消噪信号波形失真；SVD 方法中奇异值数目的选择对去噪结果影响加大，当奇异值数目较少时，降噪阶次低导致信号信息不完整，反之，降噪阶次高，噪声无法充分消除；WED 方法存在小波基选取和分解层数的限制，消噪效果具有一定的盲目性。相比于前三种消噪方法，HMMD 方法提高了运算过程中的收敛性，误差小精度高，使得原始信号的信息损失量最小，对局部信号的消噪效果好，消噪后的校正波形见图12。

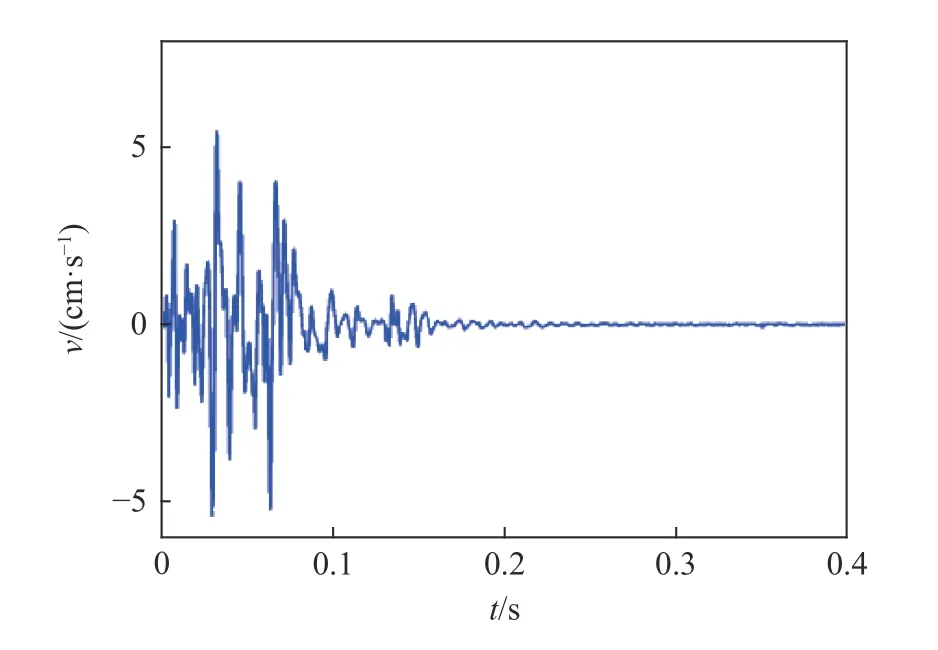
图12 消噪后的校正信号Fig.12 Baseline corrected signal after de-noising

为了验证去噪效果，分别求取原始信号、CEEMD 重组信号和HMMD 消噪后的校正信号的功率谱密度（wf）曲线，结果如图13 所示。图13 中原始信号中含有的低频基线成分致使信号在3 Hz 处出现峰值突高的奇异点，幅值为0.67 dB/Hz，远大于图13(c)中的主频峰值，且信号含有的基线成分主要位于f≤15 Hz 低频段内；图13(b)中，采用CEEMD 重组信号时，虽然对相关分量进行了相关性判别和取舍，但对高、频相关分量的处置过于随意，导致在信号的相对高频部分（大于500 Hz）中广泛分布有微幅的随机噪声，同时在信号主振频域范围内（小于500 Hz）噪声特征也较为明显；图13(c)中经过HMMD 方法消噪后的校正信号，频谱特征清晰完整，谱峰值与图13(b)幅值相当，主频由低频缓慢过渡，其中第一优势主频为16 Hz，第二优势主频为48 Hz，第三优势主频为103 Hz，具有多段别雷管起爆多次能量输入的典型频谱特征。综上所述，信号中包含的基线漂零现象的存在，会导致对信号主频峰值的误判，同时高频噪声问题对优势主频数量的确定具有显著影响。

图13 信号功率谱密度（wf）Fig.13 Power spectral density (wf) of signal

3 信号处理效果验证

3.1 基于交叉小波变换相关分析

小波多尺度相关分析可以展现不同信号总体上的相关程度，清晰描述信号在不同时域和频域上的局部细节相关特征[21]。小波多尺度相关谱综合反映了不同信号之间的相关性在时域和频域上的依赖关系，揭示不同去噪信号与原始信号在不同时间和频率尺度上的相关程度和细部特征。

为了便于分析，标识原始信号、CEEMD 重构信号和基线校正消噪信号为X1、X2和X3。图14 分别为X2、X3与X1的小波相关性凝聚谱，图中的粗实线区域表示通过显著性水平 α =0.05 条件下的红噪声标准谱的检验，箭头表示两个信号之间的位相关系，其中→表示两个信号之间为同位相，说明两者为正相关关系；←表示反位相，说明两者之间为负相关关系[22]。为避免边界效应及小波高频虚假信息，小波影响锥区域（细实线）以内为有效谱值。谱分析计算过程中，对相关性数据做归一化处理。

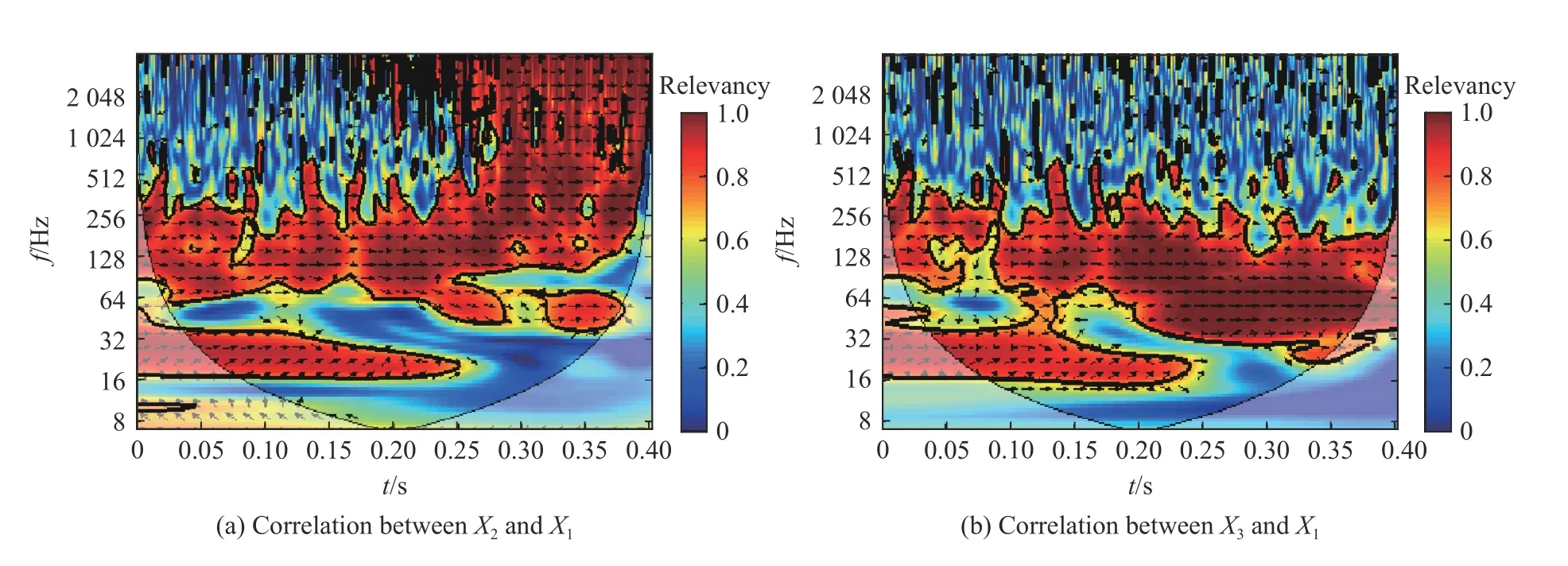
图14 信号相关性凝聚谱Fig.14 Correlation condensation spectra of signals

相关性凝聚谱说明：X2、X3和X1在不同的时域和频域尺度上均存在一定相关度。X2与X1在高频部分（大于512 Hz）正相关性显著，信号中的高频噪声未得到有效的滤除；同时X2重构过程中直接舍弃相关低频分量，导致信号低频部分信息缺失；相关性在局部出现间断、不连续现象，对信号高频噪声和低频干扰项的保留度均较高。采用文中方法得到X3与原始信号X1的相关性在时频域连续且完整，在低频尺度正相关性最为明显，显著性检验基本贯穿小波影响椎范围内的整个时频域。采用传统的互相关计算X2、X3与原始信号X1之间的相关系数分别为：0.996、0.853。验证了组合分析方法的可靠度和有效性。综上分析可知，采用交叉小波变换进行不同信号序列间的相关性分析是可行的，且能够更加清晰描述两信号序列相关关系在时域和频域变化的细部特征和共振位相差异。

3.2 进一步讨论

文中主要针对深厚表土层冻结立井基岩段爆破近区井壁振动信号开展研究，由于爆破参数的差异和井筒地质条件的复杂性，对于不同爆破条件下信号的基线漂移校正应进行相关参数的调整，以期达到最优化的分析效果。同时，随着信号各分量中基线成分的弱化，其中含有的噪声分量会被一定程度上被放大，因此，滤波消噪方法的选择对分析结果具有显著影响。在后续的研究中应注重从仪器选择、参数设置和测点布置等方面入手，从根源上避免基线漂零现象和环境噪声的产生，深入开展多种类型爆破信号的研究，以便得到更具普适性的研究成果。

4 结 论

通过对冻结立井爆破近区井壁振动信号基线和噪声分析处理，得到以下结论。

（1）测试方法的优化可一定程度上降低和控制基线漂零现象对波形特征提取的影响。传感器井壁预埋方法克服了以往井壁振动监测方法的诸多弊端，实现了井壁结构振动响应持续监测。在实际测点布置时，应重点做好仪器相关配件的防水工作，另外，对于有瓦斯涌出的矿井，应确保仪器配套供电系统的防爆性。

（2）冻结立井爆破近区井壁振动信号中基线漂零现象严重，基线成分分布在模态分解的各个分量中，且主要位于f≤15 Hz 低频段内，基线偏移会导致信号主频的误判，BEADS 方法可有效修正信号中包含的低频基线成分。基线分量的弱化会使得信号中的高频噪声在一定程度上得到放大，应采用合理的去噪方法予以消除。HMMD 消噪模型自适应性强、收敛速度快，可很大程度上消除信号中的高频噪声。

（3）交叉小波变换相关性分析可揭示两信号序列相关关系在时域和频域变化的细部特征和共振位相差异。CEEMD 重构信号易导致信号有效成分的缺失，进而导致信号振幅降低，同时高频成分保留较多。组合方法有效削弱了干扰成分对信号特征提取的影响，在信号主振时频域与原始信号关联性高，适合用于该类信号的分析处理。