负泊松比蜂窝材料抗爆炸特性及优化设计研究*

孙晓旺，陶晓晓，王显会，李进军，王利辉

（1. 南京理工大学机械工程学院，江苏 南京 210094；2. 中国人民解放军32379 部队，北京 100071；3. 中国人民解放军32381 部队，北京 100071）

当特种车辆面对地雷、简易爆炸装置等威胁时，车辆底部防护性能的优劣将直接影响车内乘坐人员的安全性[1]。三明治防雷组件是一种有效的抗爆炸冲击结构，其由两块平板及中间的夹芯层组成。前面板能够将爆炸冲击载荷分配在可压溃的芯层上，吸收大量的能量减缓冲击波[2]。Li 等[3]通过有限元模拟研究了空爆下蜂窝铝夹芯板结构的动态响应，发现夹芯层是吸收爆炸冲击能量的主要部分。

负泊松比材料是一种新型的多胞材料，在受到轴向压缩时，材料在垂直于外力方向会产生收缩现象，在受到轴向拉伸时，材料在垂直于外力方向会产生膨胀现象[4]，如图1 所示。负泊松比蜂窝是一种特殊的多孔材料，由于其具有优异的剪切模量、断裂韧性等独特的性能，在许多领域有着广泛的应用[5]。Zhou 等[6]对双箭头负泊松比结构的非线性几何特性进行了充分的研究，并采用HAM 方法成功地实现了对负泊松比结构的优化设计；杨德庆等[7]研究了星形负泊松比超材料防护结构的抗爆抗冲击性能，并发现相比于普通防护结构，负泊松比蜂窝夹芯防护结构具有更加优良的水下抗爆性能；裴连政[8]通过数值模拟与试验相结合的方法，研究了含有负泊松比蜂窝的夹芯板在空中爆炸载荷下的动态响应和吸能特性，发现负泊松比夹芯结构具有良好的爆炸防护性能；Lan 等[9]通过数值模拟比较了泡沫铝芯、六角形蜂窝芯及负泊松比蜂窝芯圆柱夹芯板在爆炸环境下的动态响应，研究发现含负泊松比蜂窝芯的圆柱面板具有更好的抗爆性能；Jin 等[10]研究了爆炸冲击下具有功能梯度的负泊松比蜂窝芯层的结构响应，并与未分级的蜂窝芯层和规则排列的蜂窝芯层进行了对比，结果显示，分级蜂窝芯层及交叉排列蜂窝芯层能够显著提高夹芯层结构的抗爆性能。研究人员前期做了一些负泊松比材料的理论和应用分析，但还很少将负泊松比蜂窝材料应用到车辆底部防护组件进行相关的爆炸分析研究。

本文中通过有限元模拟及试验介绍某车辆底部防护组件的爆炸冲击台架。然后，基于负泊松比蜂窝材料优异的抗冲击性能及吸能效果，将内凹六边形负泊松比蜂窝材料作为三明治防护组件的夹芯层部分，分析其在爆炸冲击下的结构响应及吸能特性，并与其他3 种防护组件进行对比。此外，基于遗传优化算法，建立以负泊松比胞元尺寸参数为设计变量的多目标优化模型进行优化设计。

图1 负泊松比材料受载变形示意图Fig.1 Schematic deformation of negative Poisson’s ratio material under load

1 爆炸冲击台架

1.1 爆炸冲击台架数值分析

利用有限元软件建立某车辆底部防护组件的爆炸冲击台架模型，如图2 所示，该模型中包括土壤、空气、炸药、台架、防护组件以及配重。台架整体尺寸为1 500 mm×1 860 mm×760 mm，其支撑结构采用Q235 钢焊接构成，台架上方配重8 t。防护组件布置于配重支撑梁与台架支撑脚之间，防护组件最低点离地面高度为330 mm。2 kg 柱形炸药埋于土下，炸点位于防护组件中心正下方，按照标准，炸药上表面距离土壤表面100 mm。

1.1.1 有限元模型

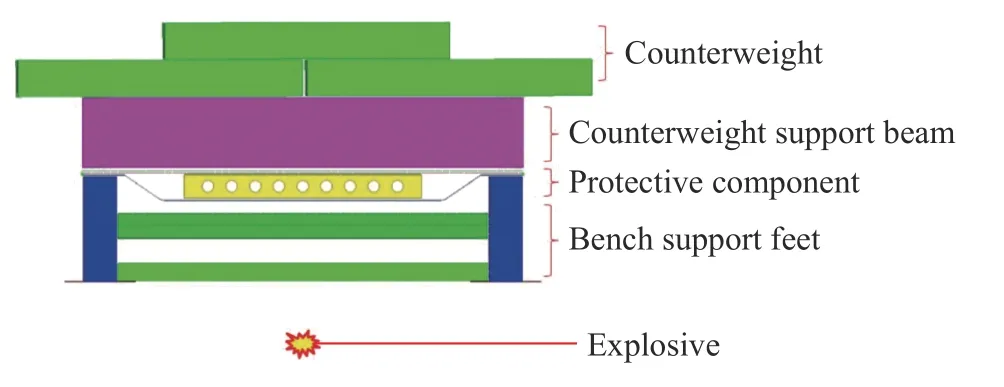
图2 爆炸冲击台架有限元模型Fig.2 A finite element model for the explosive impact bench

防护组件主要由10 mm 厚面板、8 mm 厚背板及8 mm 厚基板组成，材料分别为np500 钢、np500 钢和960E 钢，具体材料参数如表1 所示。背板与面板间距105 mm，背板与基板紧紧贴合，如图3 所示。在面板与背板中部布置一根工字支撑梁，工字梁尺寸为1 000 mm×80 mm×100 mm，材料为KS700 钢。台架各部分结构采用二维面网格进行模拟，配重以实体单元的形式进行模拟，网格单元基本尺寸为10 mm。防护组件结构之间采用*CONTACT_AUTOMATIC_SINGLE_SURFACE 来定义接触，摩擦因数设定为0.2。空气与土壤均采用六面体实体网格进行模拟，采用*C O N S R T A I N E D_LAGRANGE_IN_SOLID 关键字来定义防护组件与空气和土壤域的流固耦合。用基板来模拟战术车辆中的底甲板，若底甲板受到较大冲击，必将传递到车身，从而影响车内乘员的安全性。因此，对该试验台架主要考察爆炸冲击后防护组件的破坏情况及基板的变形情况。

基于多物质任意拉格朗日欧拉流固耦合算法（multi-material arbitrary Lagrangian-Eulerian fluid-structure interaction method，ALE-FSI）能够模拟炸药从引爆到对目标结构产生冲击的整个过程，其计算精度最高，是国内公认最成熟的爆炸数值算法[11]。因此，基于ALE-FSI 爆炸冲击数值算法，利用LS-DYNA 软件，对上述爆炸冲击台架进行数值模拟。

1.1.2 爆炸后防护组件的结构响应

数值模拟中，防护组件在受到爆炸冲击后，防护组件的面板、背板和基板都未出现结构损坏，3 块钢板的结构响应如表2 所示。爆炸产生后，面板首先受到爆炸冲击载荷作用，面板的最大挠度、最大加速度、最大动能和内能都远大于背板的。爆炸冲击波产生的能量经面板和背板吸收后作用在基板上，基板的最大挠度达到91.68 mm，图4 为基板挠度云图，最大加速度为448.52g，爆炸过程中基板的最大动能高达16.81 kJ。

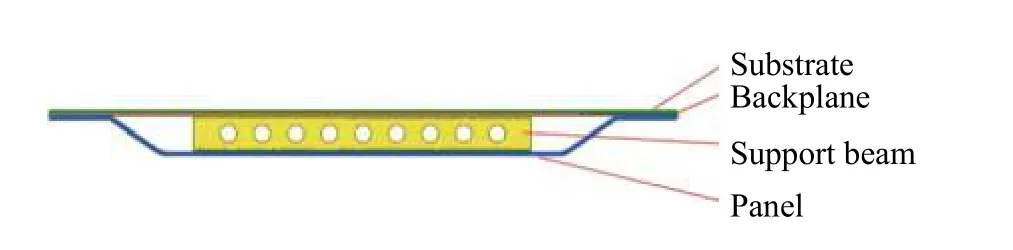
图3 防护组件示意图Fig.3 Schematic diagram of protection component

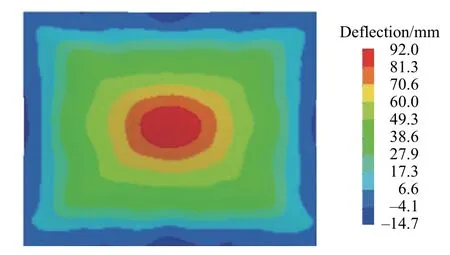
图4 基板挠度云图Fig.4 Cloud diagram of substrate deflection

表2 防护组件的结构响应与能量Table 2 Structural response and energy of protective component

1.2 台架爆炸试验

为验证数值模型的准确性，布置了如图5 所示的爆炸冲击试验台架。试验中台架结构、材料、配置及炸药布置等均与数值计算中保持一致。在台架基板上方中部安装应变梳，测量基板在爆炸过程中的动态变形，如图6 所示。

试验后，台架整体未出现明显的结构损坏与焊缝失效等现象，计算结果与试验结果比较吻合。测量基板上方安装的应变梳的最大挠度约为89 mm，如图7 所示，可以作为爆炸过程中基板的最大动态变形。计算中，基板中心处产生了较大弹性变形，最大挠度为91.96 mm，数值计算与试验相比误差为3.11%，误差在可接受范围内。综上所述，对比试验现象，计算精度能够满足要求，通过ALE-FSI 算法来模拟爆炸冲击下防护组件的结构响应是合理的。

图6 应变梳布置Fig.6 Strain comb arrangement

图5 爆炸冲击试验台架Fig.5 Explosive impact test bench

图7 试验后应变梳Fig.7 Strain comb after test

2 内凹六边形蜂窝材料夹芯防护组件

上述防护组件中，虽然面板与背板吸收了爆炸冲击产生的大量能量，但基板挠度仍然较大，基板的最大加速度高达448.52g，最大动能超过16 kJ，若将此防护组件布置到车辆底部、车身侧围和地板等关键位置必将受到较高冲击，从而增大车内乘员受伤的风险。

为了提高防护组件的防护能力，在不改变其整体结构的情况下，在背板与面板之间添加负泊松比蜂窝夹芯材料，并在两侧增加夹芯固定件，如图8 所示，内凹六边形负泊松比蜂窝材料局部结构示意图如图9 所示。内凹六边形蜂窝与夹芯固定件的基体材料都为H14 铝，材料参数如表3 所示。计算中，防护组件各部分之间的接触类型及模型的边界条件保持不变。

图8 负泊松比蜂窝夹芯防护组件Fig.8 Negative Poisson’s ratio honeycomb sandwich protection component

图9 负泊松比蜂窝夹芯材料局部结构Fig.9 Local structure of honeycomb sandwich material with negative Poisson’s ratio

表3 H14 铝材料参数Table 3 H14 aluminum material parameters

2.1 内凹六边形负泊松比蜂窝材料胞元

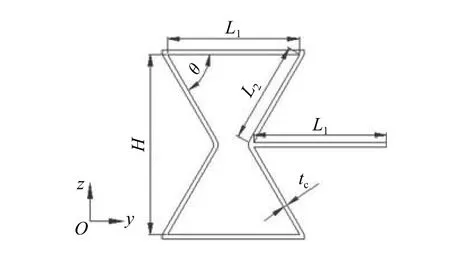
图10 胞元几何参数示意图Fig.10 Schematic diagram of cell geometric parameters

内凹六边形负泊松比蜂窝材料胞元结构几何参数如图10 所示。其中，水平胞壁的长度为L1，弯曲胞壁的长度为 L2，水平胞壁与弯曲胞壁之间的夹角为胞壁夹角 θ ，弯曲胞壁与水平胞壁的壁厚相等，称为胞元壁厚 tc。

图10 中所示几何参数必须满足式（1）时，才能使胞元结构满足内凹特性且具有一定的可变行程[12]。

2.2 内凹六边形负泊松比蜂窝夹芯防护组件爆炸计算模型

研究中，在防护组件背板与面板之间布置的内凹六边形蜂窝材料胞元结构几何参数为：水平胞壁长度 L1=22.5 mm ，弯曲胞壁长度 L2=17.32 mm ，胞壁厚度tc=0.32 mm ，胞元夹角θ =60◦；蜂窝在垂直于胞元方向上的延伸长度为1 000 mm，在z 向上布置胞元3 层，蜂窝结构总高度为90 mm，芯层整体从中间位置被支撑梁分成两部分，总重量为15.03 kg，如图9 所示。

图11 爆炸冲击下负泊松比蜂窝防护组件典型变形模式Fig.11 Typical deformation mode of Poisson’s ratio honeycomb protection component under explosion impact

图12 负泊松比蜂窝芯层中心变形图Fig.12 Deformation diagram of negative Poisson’s ratio honeycomb core center

内凹六边形负泊松比蜂窝防护组件在爆炸冲击下的典型变形模式如图11 所示，图12 为负泊松比蜂窝芯层中心部分的变形图，结合图13 所示的防护组件各部分结构的动能时程曲线，来更好地理解负泊松比蜂窝及整个防护组件在爆炸冲击下的结构响应。爆炸产生的球形冲击波在0.4 ms 时首先作用在面板上，面板上动能也随之开始增大；在0.1 ms 之后蜂窝芯层底部中心开始被压缩，蜂窝芯层动能开始增大；在爆炸发生后的1.5 ms，蜂窝芯层中心区域继续被压缩，由于蜂窝材料的负泊松比效应，中心断开处出现向内收缩的趋势，如图12 所示，背板、基板开始产生变形，动能开始增大；随着爆炸冲击波继续扩散，在爆炸发生后的2.0 ms～3.5 ms，面板部分区域出现回弹，其动能开始减小，远离爆炸中心的蜂窝芯层边缘处也开始被压缩，两侧的蜂窝结构开始向内收缩,负泊松比蜂窝致密到中心加载区域，蜂窝芯层的动能也达到峰值，背板、面板的变形及动能继续增大；在爆炸发生后的4.0 ms，芯层边缘处的材料快速向内收缩，而蜂窝在载荷冲击方向被压缩量已达峰值且基本维持不变，蜂窝整体的动能也开始减小，与此同时，背板与基板的变形持续增大，传递到背板与面板的动能继续增加；直到爆炸发生后5.0 ms，蜂窝芯层在载荷冲击方向和垂直载荷方向的压缩量基本维持不变，至此蜂窝芯层完全被压实，在横向和纵向上皆无可变形空间，此时背板与基板的动能也达到峰值。

含有负泊松比蜂窝夹芯层的防护组件在2 kg 柱形炸药爆炸冲击下的结构响应与能量的变化，如表4 所示。爆炸发生后，内凹六边形负泊松比蜂窝被压缩，材料拉入局部加载区域，更加适应动态载荷，与此同时夹芯层的内能持续增大，最大超过40 kJ，如图14 所示。在爆炸冲击吸能结构设计中，比吸能（specific energy absorption，SEA）意为结构单位质量吸收的能量[13]，是衡量抗爆性的重要指标，可用下式表示：

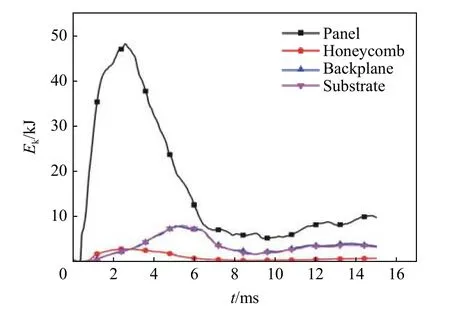
图13 防护组件各部分结构动能时程曲线Fig.13 Time history curve of the kinetic energy of each part of the protective component

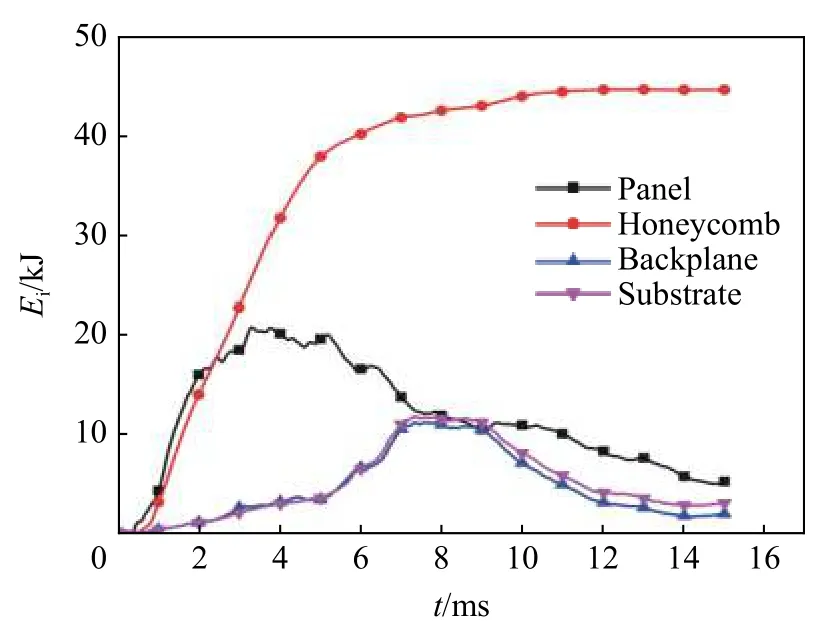
图14 防护组件各部分结构内能时程曲线Fig.14 Time history curve of the internal energy of each part of the protective components

式中： Etotal为结构整体吸收的总能量， Mtotal为结构的总质量。

表4 防护组件的结构响应与能量Table 4 Structural response and energy of protective components

比吸能越大，说明该结构的吸能效率越高。由表4 可知，内凹六边形负泊松比蜂窝夹芯层的吸能效率远大于防护组件其他结构的吸能效率。

通过数值模拟提取的原始方案防护组件与含有负泊松比蜂窝夹芯材料的防护组件基板中心挠度及基板动能时程曲线如图15～16 所示，相比于原始防护组件，经过负泊松比蜂窝夹芯层防护组件吸能的基板，其最大挠度降低了13.72 mm，最大动能降低了52.17%。

通过对含有负泊松比蜂窝材料夹芯层的防护组件进行数值分析，研究发现，蜂窝夹芯层的吸能效率远高于防护组件中其他结构的吸能效率，且能够有效降低基板的挠度及动能。若将此类防护组件布置于车辆底部，车辆在面临爆炸威胁时，该防护组件能够起到很好的吸能效果，从而降低车身结构受到的冲击，进而降低车内乘员受到的损伤。

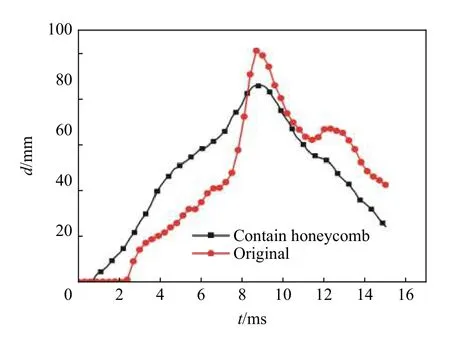
图15 两种防护组件基板中心挠度时程曲线Fig.15 Time history curve of the center deflection of the two kinds of protective component’s substrates

图16 两种防护组件基板动能时程曲线Fig.16 Time history curve of the kinetic energy of the two kinds of protective component’s substrates

2.3 相同质量下不同防护组件防护效果比较

为了验证内凹六边形负泊松比蜂窝材料在抗爆炸冲击台架中防护效果的优越性，在防护组件总质量相同的前提下进行了以下3 组2 kg 炸药台架爆炸的数值模拟。T1：面板厚度增大至10.69 mm；T2：背板厚度增大至8.69 mm；T3：将内凹六边形负泊松比蜂窝芯层替换为等质量的正六边形蜂窝芯层。

其中，图17 所示为正六边形蜂窝芯层部分结构，其整体结构设置为3 层，整体尺寸与内凹六边形负泊松比蜂窝材料基本保持一致，基体材料为H14 铝。正六边形蜂窝胞元结构几何尺寸如图18 所示，正六边形边长 L1=22.5 mm ，胞元夹角 θ=120◦，胞元壁厚 tc=0.67 mm 。

图17 正六边形蜂窝芯层部分结构Fig.17 Partial structure of regular hexagonal honeycomb core layer

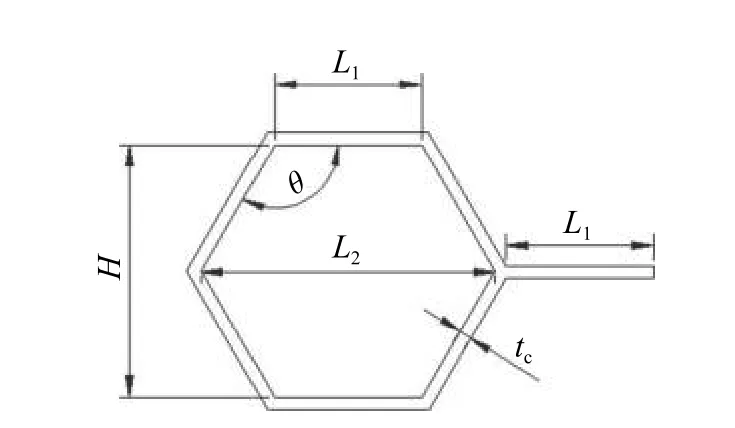
图18 正六边形蜂窝胞元结构示意图Fig.18 Schematic diagram of a regular hexagonal honeycomb cell structure

图19、20 分别为数值模拟提取的4 种防护组件基板中心的挠度时程曲线和基板动能时程曲线。其中，将内凹六边形负泊松比蜂窝芯层材料的质量附在面板和背板上的防护组件在受到爆炸冲击后，基板的最大挠度分别为88.42、87.28 mm，传递到基板的最大动能分别为12.44、12.48 kJ。正六边形蜂窝芯层防护组件在受到爆炸冲击后，基板的最大挠度为80.83 mm，基板的最大动能为9.38 kJ。在上述3 种防护组件中，正六边形蜂窝芯层的防护组件的防护效果优于其他两种不加芯层的防护组件，但在同样工况同等质量情况下，与内凹六边形负泊松比蜂窝结构的防护组件相比，其基板的最大挠度及最大动能仍然明显更高。

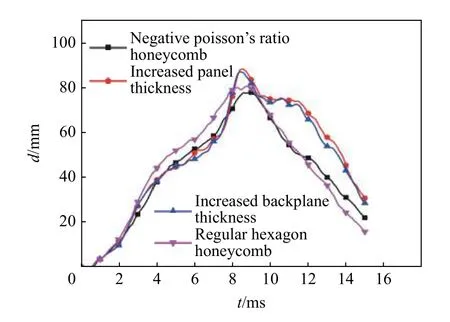
图19 4 种防护组件基板中心挠度时程曲线Fig.19 Time history curves of center deflection of four kinds of protective component’s substrates

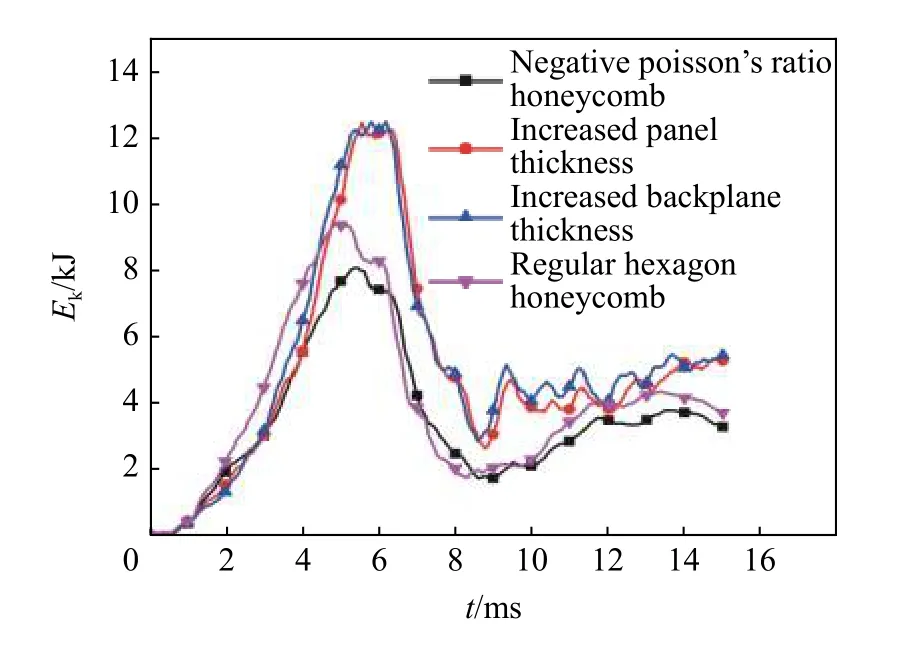
图20 4 种防护组件基板动能时程曲线Fig.20 Time history curves of kinetic energy of four kinds of protective component’s substrates

3 内凹六边形负泊松比蜂窝结构多目标优化设计

韩会龙等[14]通过数值分析负泊松比蜂窝材料的动力学响应及能量吸收特性，发现改变胞元微结构可以提升负泊松比蜂窝的能量吸收能力。针对前文中的防护组件爆炸冲击台架，通过对内凹六边形负泊松比结构的胞元几何参数进行优化设计，提高负泊松比蜂窝结构的整体吸能效果，进而降低基板的最大挠度及最大动能。在确定设计变量、变量范围及优化目标的基础上，采用D-optimal 试验设计对变量进行采样，然后根据计算得到的样本采用Kinging 法构建代理模型，通过非支配排序遗传算法（NSGA-Ⅱ）来求解优化目标的Pareto 解集，得到内凹六边形负泊松比蜂窝结构多目标优化的最优解。

3.1 内凹六边形负泊松比蜂窝结构优化数学模型

负泊松比胞元的水平胞壁的长度 L1、弯曲胞壁的长度L2、胞元壁厚tc、胞壁夹角θ 为设计变量，其中， L1、 L2及 tc为连续变量， θ 为离散变量，且变量之间应满足 L1≥2L2cos θ 。内凹六边形负泊松比蜂窝结构的优化设计目的是降低基板的最大挠度及最大动能，同时使蜂窝夹芯层的总质量限制在一定范围内。因此，根据设计目标、约束条件、设计变量确定了多目标优化数学模型如下式：

式中： Fd(x) 为基板的z 向最大变形量， FE(x) 为基板的最大动能，M 为蜂窝夹芯的总质量， M∗为蜂窝夹芯的约束质量，设定为20 kg。在优化设计中，使得各目标函数最小，从而达到防护组件性能最好的要求。

3.2 基于D-optimal 采样试验设计

试验设计（是结构优化设计中重要的统计方法，主要用于选择合适的试验参数、确定最佳的参数组合、分析设计参数与响应结果之间的关系以及构建相应的代理模型来代替大计算量的实际模型进行求解等。本文中采用D-optimal 试验设计方法来选取试验样点，为得到更加可靠的试验设计，要让选取的试验点可使模型的渐进协方差矩阵的行列式最小[15]。优化设计的设计变量有4 个，采用D-optimal 采样方法获得28 组设计变量的组合形式及计算结果如表5 所示。

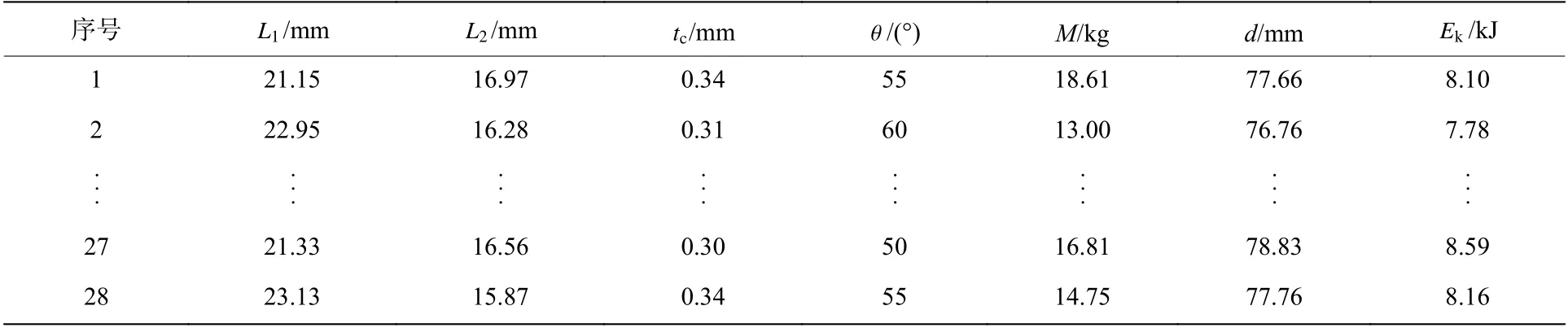
表5 基于D-optimal 采样的试验设计及结果Table 5 Experimental design and results based on D-optimal sampling

3.3 优化目标代理模型建立

Kringing 代理模型是一种估计方差最小的无偏代理模型。该方法可以描述防护组件爆炸仿真这样的高度非线性动态过程[16]。利用有限元软件将每组采样点计算得出响应值，采用Kringing 法构造代理模型后，一般采用决定系数 R2来评估代理模型的拟合精度，其中决定系数表达式为：

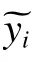
R2值越接近于1，代理模型精度越高[17]。由表6 可知，代理模型各目标响应的决定系数R2都大于0.95，因此代理模型符合精度要求。

表6 目标响应的决定系数Table 6 Decision coefficients of target response

3.4 基于NSGA-Ⅱ算法的内凹六边形负泊松比结构优化计算及分析

在构建代理模型后，本文利用非支配排序遗传算法（NSGA-Ⅱ）来求解优化目标的Pareto 解集。NSGA-Ⅱ算法运行速度快、计算复杂度低、易于实现，已成为多目标优化算法的基准之一，广泛应用于科学研究及工程实践领域[18]。在求解多目标优化问题时，通常不能获得唯一的最优解，得到的多个无法简单进行比较的解集即为帕累托（Pareto）最优解。在运用NSGA-Ⅱ算法求解时设置Pareto 解集数为1 000 个，遗传代数为50 代，每代精英数量占样本空间的10%，遗传变异率为0.01。最终得到帕累托解集858 个，帕累托前沿如图21 所示。在车辆底部爆炸防护中，最重要的是降低车内乘员损伤，起决定作用的是传递到车身的冲击能量，因此本文优化结果更加注重降低基板的动能，从而筛选出第50 代第156 组为内凹六边形负泊松比蜂窝夹芯优化的最优解，如表7 所示。最优解对应的水平胞壁长度为20.43 mm，弯曲胞壁长度为18.11 mm，胞壁厚度为0.32 mm，胞壁夹角为50°。

3.5 优化结果验证

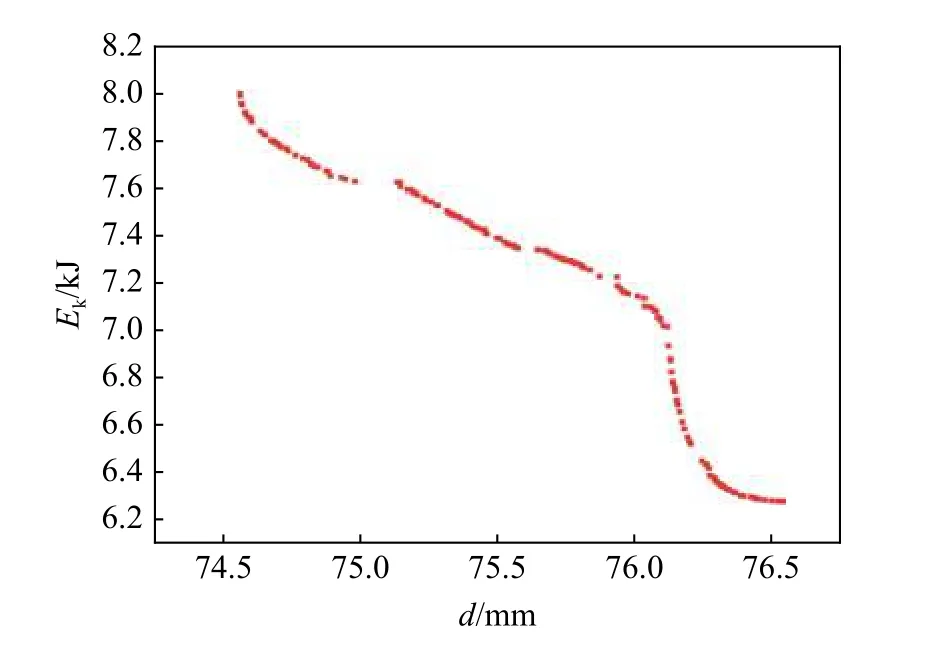
图21 帕累托前沿Fig.21 Pareto front

表7 第50 代Pareto 解集（部分）及变量参数Table 7 The 50th generation Pareto solution set (part) and variable parameters

为了验证内凹六边形负泊松比蜂窝夹芯材料多目标优化结果的准确性，根据3.4 节优化结果得到的设计变量参数，建立爆炸冲击台架有限元模型，求解后与优化结果对比。基板最大挠度的优化结果和数值模拟结果分别为76.23 和74.58 mm，相对误差为2.16%；基板最大动能分别为6.52 和6.41 kJ，相对误差为1.69%，误差皆小于5%，因此可以认为优化结果具有较高的准确性。如图22～23 所示，优化后新方案的基板最大挠度为74.58 mm，相比于优化前降低了4.34%；基板的最大动能为6.41 kJ，相比于优化前降低了20.27%。

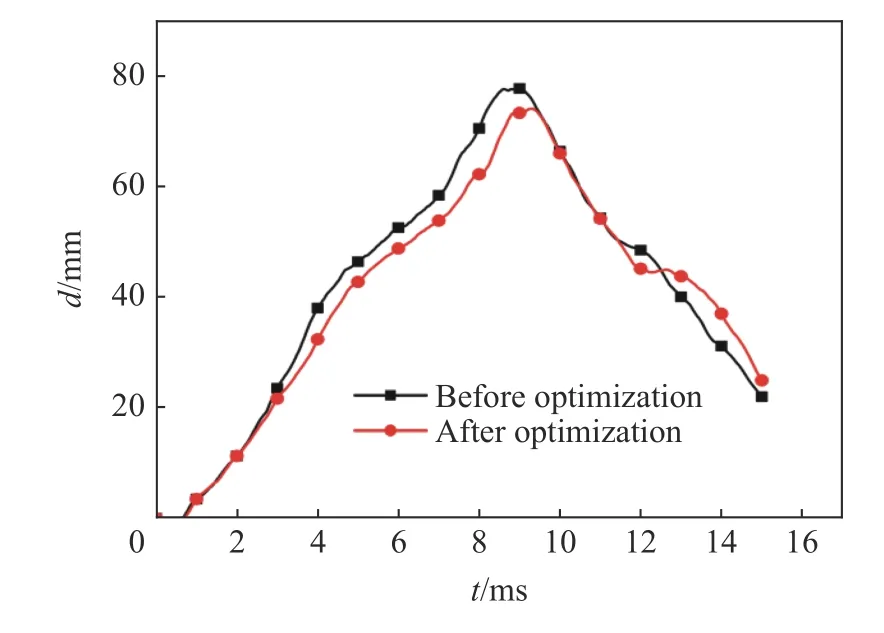
图22 优化前后基板挠度时程曲线Fig.22 Time history curves of substrate deflection before and after optimization

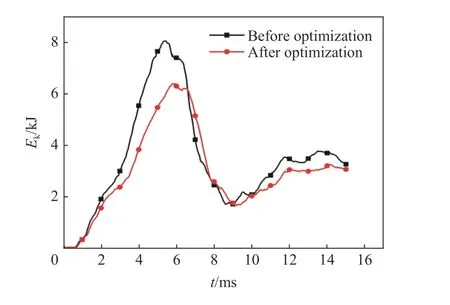
图23 优化前后基板动能时程曲线Fig.23 Time history curves of substrate kinetic energy before and after optimization

4 结 论

本文基于车辆底部防护组件爆炸冲击台架，提出了一种将内凹六边形负泊松比蜂窝材料作为其夹芯层的防护组件，分析了防护组件在2 kg 柱形炸药爆炸冲击下的结构响应；通过NSGA-Ⅱ遗传算法求解基于负泊松比胞元尺寸参数的多目标优化问题，得到基板最大挠度与基板最大动能的Pareto 前沿并选出最优解。研究表明：（1）相比于不含夹芯结构的防护组件，内凹六边形负泊松比蜂窝防护组件能够有效降低基板的最大挠度及动能，且负泊松比蜂窝夹芯在整个防护组件中的比吸能远大于面板和背板。（2）同等质量的前提下，相比于正六边形蜂窝夹芯等其他3 种防护组件，内凹六边形负泊松比蜂窝夹芯防护组件的防护效果更优。（3）在满足优化要求的前提下，成功实现了对负泊松比夹芯层结构的多目标优化，优化后基板的最大挠度降低了4.34%，基板的最大动能降低了20.27%。

参考文献：李补莲, 原树兴. 现代军用车辆的防护措施 [J]. 国外坦克, 2011(5): 41-43. DOI: CNKI:SUN:GWTK.0.2011-05-019.

[1]LI B L, YUAN S X. Protective measures of modern military vehicles [J]. Foreign Tanks, 2011(5): 41-43. DOI:CNKI:SUN:GWTK.0.2011-05-019.

[2]IMBALZANO G, LINFORTH S, NGO T D, et al. Blast resistance of auxetic and honeycomb sandwich panels: comparisons and parametric designs [J]. Composite Structures, 2018, 183: 242-261. DOI: 10.1016/j.compstruct.2017.03.018.

[3]LI X, ZHANG P, WANG Z, et al. Dynamic behavior of aluminum honeycomb sandwich panels under air blast: experiment and numerical analysis [J]. Composite Structures, 2014, 108: 1001-1008. DOI: 10.1016/j.compstruct.2013.10.034.

[4]周冠. 新型负泊松比结构关键技术研究及其在车身设计中的应用[D]. 长沙: 湖南大学, 2015: 6−7.

[5]QIAO J, CHEN C Q. Analyses on the in-plane impact resistance of auxetic double arrowhead honeycombs [J]. Journal of Applied Mechanics, 2015, 82(5): 051007. DOI: 10.1115/1.4030007.

[6]ZHOU G, MA Z D, GU J, et al. Design optimization of a NPR structure based on HAM optimization method [J]. Structural and Multidisciplinary Optimization, 2016, 53(3): 635-643. DOI: 10.1007/s00158-015-1341-x.

[7]杨德庆, 吴秉鸿, 张相闻. 星型负泊松比超材料防护结构抗爆抗冲击性能研究 [J]. 爆炸与冲击, 2019, 39(6): 124-135.DOI: 10.11883/bjycj-2018-0060.YANG D Q, WU B H, ZHANG X W. Explosion and impact resistance of star negative Poisson’s ratio metamaterial protective structure [J]. Explosion and Shock Waves, 2019, 39(6): 124-135. DOI: 10.11883/bjycj-2018-0060.

[8]裴连政. 负泊松比夹芯板抗爆性能实验与仿真研究[D]. 大连: 大连理工大学, 2016: 11−34.

[9]LAN X K, FENG S S, HUANG Q, et al. A comparative study of blast resistance of cylindrical sandwich panels with aluminum foam and auxetic honeycomb cores [J]. Aerospace Science and Technology, 2019, 87: 37-47. DOI: 10.1016/j.ast.2019.01.031.

[10]JIN X C, WANG Z H, NING J G, et al. Dynamic response of sandwich structures with graded auxetic honeycomb cores under blast loading [J]. Composites Part B: Engineering, 2016, 106: 206-217. DOI: 10.1016/j.compositesb.2016.09.037.

[11]魏然. 爆炸冲击下车身结构防护机理及多学科优化研究[D]. 南京: 南京理工大学, 2019: 3−4.

[12]王陶. 负泊松比结构力学特性研究及其在商用车耐撞性优化设计中的应用[D]. 南京: 南京理工大学, 2018: 21−22.

[13]ZHOU G, MA Z D, LI G, et al. Design optimization of a novel NPR crash box based on multi-objective genetic algorithm [J].Structural and Multidisciplinary Optimization, 2016, 54(3): 673-684. DOI: 10.1007/s00158-016-1452-z.

[14]韩会龙, 张新春, 王鹏. 负泊松比蜂窝材料的动力学响应及能量吸收特性 [J]. 爆炸与冲击, 2019, 39(1): 47-57. DOI:10.11883/bzycj-2017-0281.HAN H L, ZHANG X C, WANG P. Dynamic response and energy absorption characteristics of negative Poisson’s ratio honeycomb materials [J]. Explosion and Shock Waves, 2019, 39(1): 47-57. DOI: 10.11883/bzycj-2017-0281.

[15]田永军, 段国林, 夏晓光, 等. 响应面模型与混合优化算法相结合的锯片参数优化设计 [J]. 中国机械工程, 2016, 27(22):3025-3031. DOI: 10.3969/j.issn.1004-132X.2016.22.008.TIAN Y J, DUAN G L, XIA X G, et al. Optimization design of saw blade parameters based on response surface model and hybrid optimization algorithm [J]. China Mechanical Engineering, 2016, 27(22): 3025-3031. DOI: 10.3969/j.issn.1004-132X.2016.22.008.

[16]SIMPSON T W, MAUERY T M, KORTE J J, et al. Kriging models for global approximation in simulation-based multidisciplinary design optimization [J]. AIAA Journal, 2001, 39(12): 2233-2241. DOI: 10.2514/2.1234.

[17]任朋飞. 抗冲击型车身柔性底部结构防护技术研究[D]. 南京: 南京理工大学, 2018: 54−55.

[18]詹长书, 王清. 基于改进遗传算法电动汽车变速器参数设计与优化 [J]. 重庆理工大学学报(自然科学版), 2020, 34(2):1-5. DOI: 10.3969/j.issn.1674-8425(z).2020.02.001.ZHAN C S, WANG Q. Design and optimization of transmission parameters of electric vehicle based on improved genetic algotithm [J]. Journal of Chongqing Institute of Technology (Natural Science), 2020, 34(2): 1-5. DOI: 10.3969/j.issn.1674-8425(z).2020.02.001.