基于EMD 改进算法的爆破振动信号去噪*

易文华，刘连生，闫 雷，董斌斌

（江西理工大学资源与环境工程学院，江西 赣州 341000）

露天爆破施工过程中，由于测振仪器受到外界及自身因素的干扰，爆破振动信号包含了各种频率成分的信息，反映了爆破特征和周边环境对振动的影响，若直接对信号进行时频分析，则会掺杂诸多干扰因素，影响分析效果，因此有必要对信号进行科学的去噪。

目前常用的信号去噪方法有傅里叶变换[1]、短时傅里叶变换[2]、小波去噪[3]、小波包去噪[4]、经验模态分解(empirical mode decomposition, EMD)滤波去噪[5]等，其中，傅里叶变换[1]是处理信号噪声最传统的方法，但傅里叶变换只能在频域内进行分析，若信号在时域上某处发生突变，则无法分辨信号的尖峰是突变还是噪声导致。而短时傅里叶变换[2]通过构建窗函数具备了时域的局部分析能力，但短时傅里叶变换的窗函数一旦确定后便只有单一的分辨率，故其对爆破振动这类非平稳信号分析结果误差较大。小波变换[3]可以对信号在时域和频域内进行分析，能更好地进行去噪，但小波变换分解的精度依赖小波基的选择，选择不同的小波基会产生不同精度的误差。而小波包[4]能够同时对信号的低频和高频部分进行细分，具有比小波更高的精度，因此去噪能力相比于小波也有所增强。EMD 滤波去噪[5]能自适应地将信号按不同时间尺度进行分解，可以很好地提取非平稳信号变化的特征；与小波、小波包去噪相比，EMD 去噪不需要选择基函数且自适应性强。但EMD 在去噪的过程中分解出的固有模态函数(intrinsic mode function, IMF)分量之间出现模态混叠现象[6-7]，对去噪效果会产生影响。为了解决IMF 分量模态混叠问题，曹莹等[6]提出了基于形态滤波预处理与端点延拓相结合的方法，来抑制IMF 分量之间的混叠现象，但需要根据实际情况对匹配误差取不同的限值，若取值不合适，则会与信号实际趋势产生很大的误差。Wu 等[7]提出了集总经验模态分解(ensemble empirical mode decomposition，EEMD)方法抑制IMF 分量之间的混叠现象，但需要预先算出信号的信噪比，且对低频率比混合信号抑制效果不佳。

由于李晓斌等[8]采用了正交指数判别法研究了IMF 分量之间的正交性，得出了混叠的IMF 分量不正交，不混叠的IMF 分量正交，因此分解出的IMF 分量之间是否具有混叠现象可由正交性来判断，而主成分分析(principal component analysis, PCA)[9-12]能将具有相关性的数组转化为正交数组。因此本文中以振动信号EMD 滤波去噪效果不佳为研究对象，利用PCA 的正交性对EMD 进行改进，提出一种基于PCA 和EMD 的改进算法PEMD，通过模拟信号和爆破实测信号分析与EMD、EEMD[13]进行去噪效果对比，检验和评价改进算法的去噪效果。

1 PEMD 算法的设计与构建

PEMD 是基于PCA 对EMD 滤波去噪过程中所存在的模态混叠现象进行改进的算法。PCA[9]是将一组高维向量通过一个特殊的特征向量矩阵，用一组低维向量来表示，并且只损失极少部分信息或次要信息。EMD 滤波去噪是对分解出的IMF 分量进行筛选，但各IMF 分量之间不完全正交导致信息重叠，从而影响滤波效果。由于PCA 可将大量相关性的高维数组变换为正交的低维特征分量的集合，因此PCA[11-12]能够将混叠的IMF 分量组合转化为完全正交的主成分变量集合，从而消除了模态混叠现象，提高了滤波去噪的效果。

PEMD 算法的实现步骤如图1 所示。

（1）将原始信号 x(t) 通过EMD 分解成m 个IMF 指标，每个分量都取 n 个评价对象。

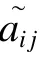
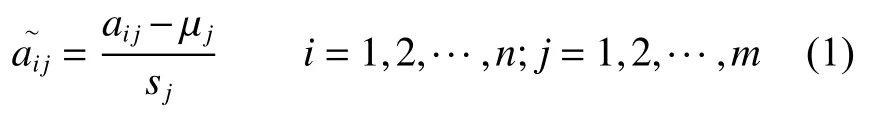
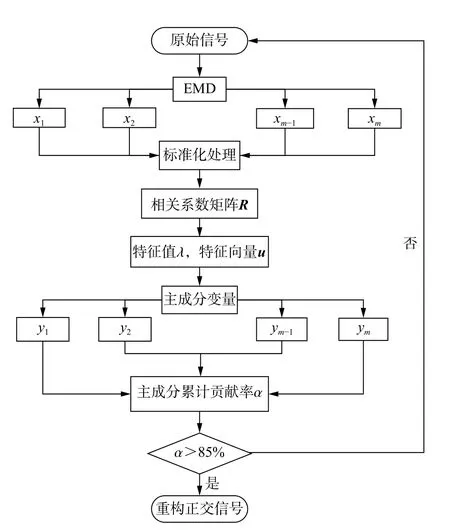
图1 PEMD 算法流程图Fig.1 PEMD algorithm flow chart

式中： µj为第j 个指标样本均值， sj为第j 个指标样本标准差。

同时，将指标变量进行标准化处理，即：

（3）计算相关系数矩阵 R ：

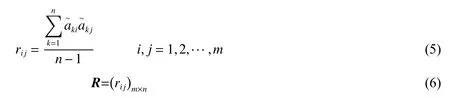
（4）计算相关系数矩阵的特征值λ 和特征向量u，由特征向量组成m 个新的正交主成分变量yi(i=1,2,···,m) ：

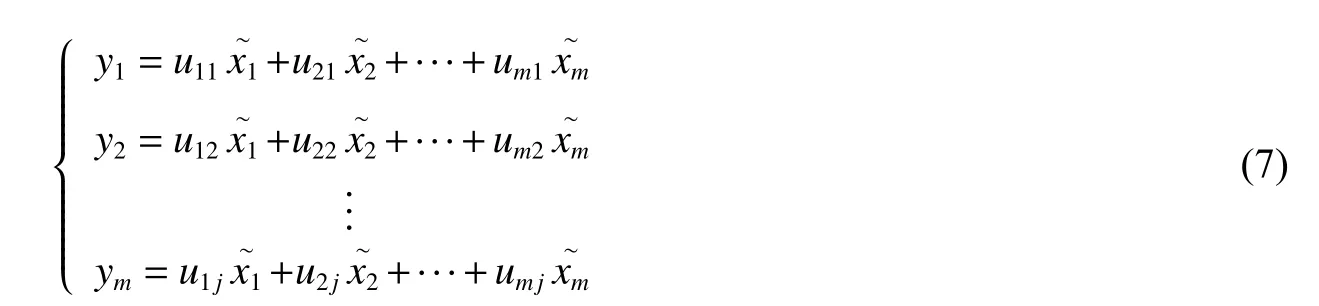
（5）选择p 个正交主成分变量，计算主成分累计贡献率αp：

式中：bj为第j 个正交主成分变量的信息贡献率，αp为前p 个正交主成分变量的累计贡献率。

（6）选择累计贡献率αp达到85%[9,14]以上的正交主成分变量组合，对其进行信号重构，生成新的正交信号 x′(t) 。

（7）对新的正交信号 x′(t) 进行EMD 分解，得到完全正交的IMF 分量。

2 数值模拟

2.1 模态混叠的验证与消除

仿真过程中，采样频率设为1 024 Hz，采样点数为1 000 个，信号长度约1 s。仿真信号采用正弦信号x1(t)=8sin(60πt) 和一维概率密度为 p(x) 的高斯白噪声混合而成，记为 x(t) ，其中：

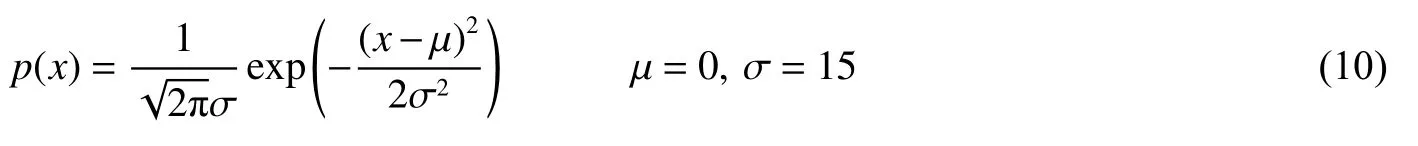
对仿真信号 x(t) 进行EMD 分解，得到9 个IMF 分量 x1,x2,···x9和对应的频谱，如图2 所示。

图2 仿真信号IMF 分量与频谱Fig.2 IMF component and spectrum of simulation signal

从图2 可以看出， x1与 x2分量混有大量的噪声， x3含有部分仿真信号特征，受到了噪声的干扰，其对应的频谱具有多种主频，出现了模态混叠现象。

为了消除混叠现象以达到更好的滤波去噪效果，在此采用PEMD 改进算法对仿真信号进行处理。首先将仿真信号 x(t) 和 x1,x2,···x9分量做主成分分析，通过第1 节算法步骤得到主成分变量 y1,y2,···,y9的信息贡献率，如表1 所示。

表1 主成分变量信息贡献率Table 1 Principal component variable information contribution rate

由表1 可知，前8 个主成分变量信息贡献率已达到85%[9,14]，因此取前8 个主成分对仿真信号进行重构，得到正交的仿真信号 x′(t) ，继而对其进行EMD 分解，得到IMF 分量频谱图，并与仿真信号频谱进行对比，如图3 所示。

从图3 可以看出，与仿真信号相比，正交信号分解出的 x3分量频谱具有单一主频，从而消除了仿真信号 x3分量的模态混叠现象。因此，PEMD 算法能够有效地消除EMD 分解的模态混叠现象，使信号的各种成分能够独立地分配到单一的IMF 分量中，即分解出的噪声和振动信号会完全分离到不同的IMF 分量中，从而可以凭借噪声与振动信号的自相关函数特性识别出只含噪声的IMF 分量，为进一步有效地选择IMF 分量组合达到较好的滤波去噪效果提供参考。

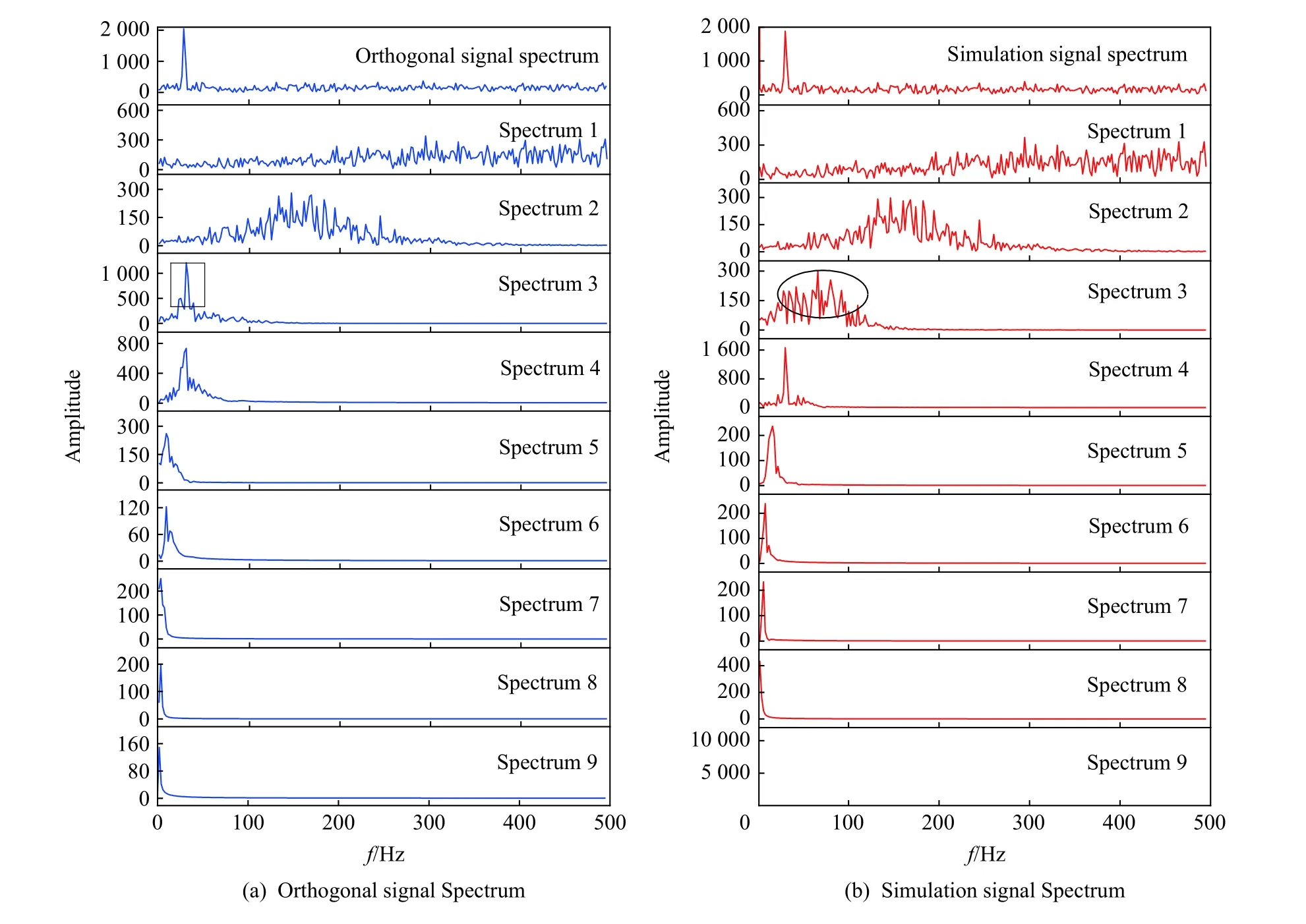
图3 正交信号与仿真信号频谱对比Fig.3 Spectrum comparison between orthogonal signal and simulated signal

2.2 去噪

2.2.1 噪声分量的识别与振动信号的重构

为了识别出噪声分量，对EMD 和PEMD 分解出的IMF 分量进行自相关分析[15]，做出各IMF 分量的自相关函数特性曲线，并引入同样能去除模态混叠现象的EEMD[13]算法进行对比，如图4 所示。

由图4 可知，EMD 和EEMD 分解出的 x1与 x2的自相关函数符合高斯白噪声的特性， x3既含有噪声特性又包含了振动信号的波动特性，在保证滤波去噪不失真的前提下，保留 x3分量，最后一个分量通常为信号的趋势项，也加以滤除，因此选择 x3～x8的组合进行重构，得到滤波去噪信号；PEMD 分解出的 x1与x2为高斯白噪声， x3明显没有高斯白噪声特性，去掉趋势项后，选择 x3～x9组合进行重构。

2.2.2 去噪效果对比

由于仪器采集的原始信号一般为时域信号，且仿真信号中的正弦信号时域特征明显，因此可用EMD、EEMD 和PEMD 三种去噪方法的时域分析来评估去噪效果，如图5 所示。

由于振动信号去噪效果多用信噪比γ 和均方根误差σ 指标[16]来评价，其中：

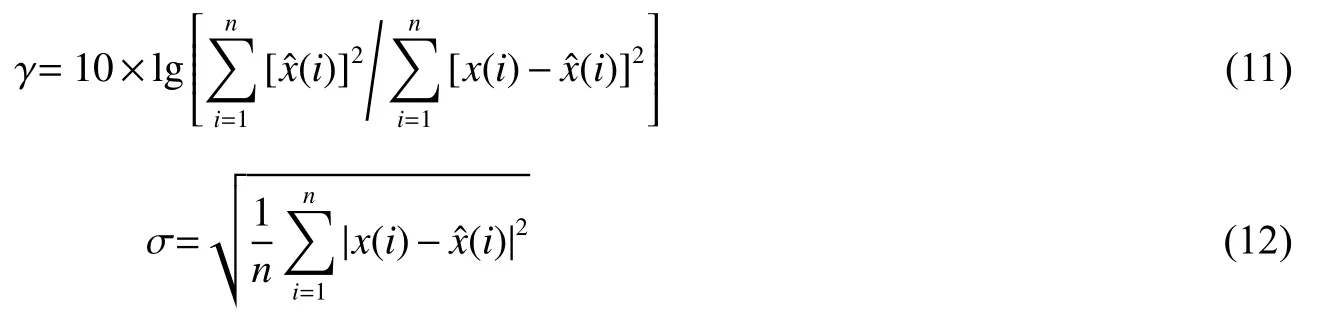
因此计算三种去噪方法的评价指标如表2 所示。

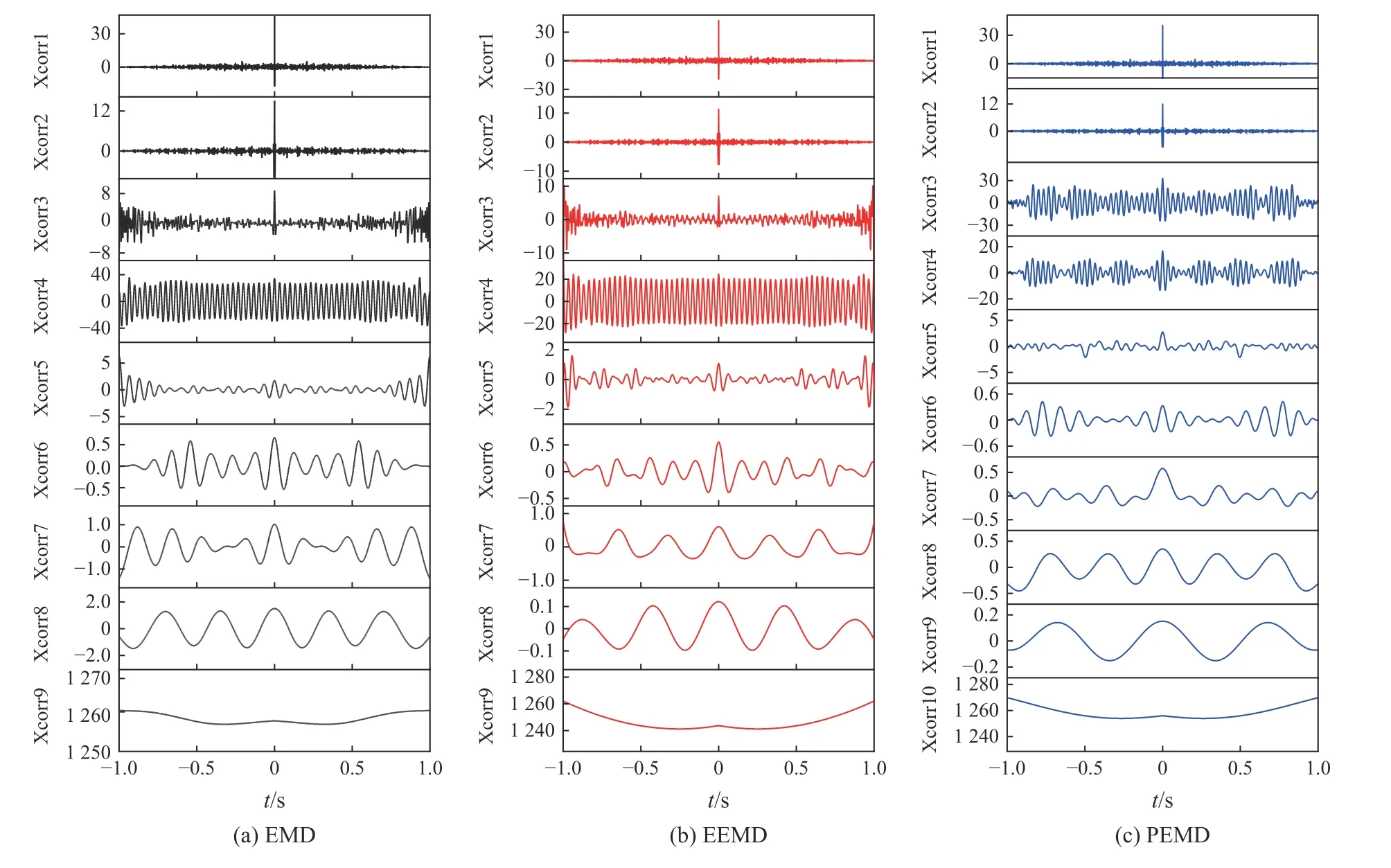
图4 IMF 分量自相关函数特性曲线Fig.4 Characteristic curves of IMF component autocorrelation function

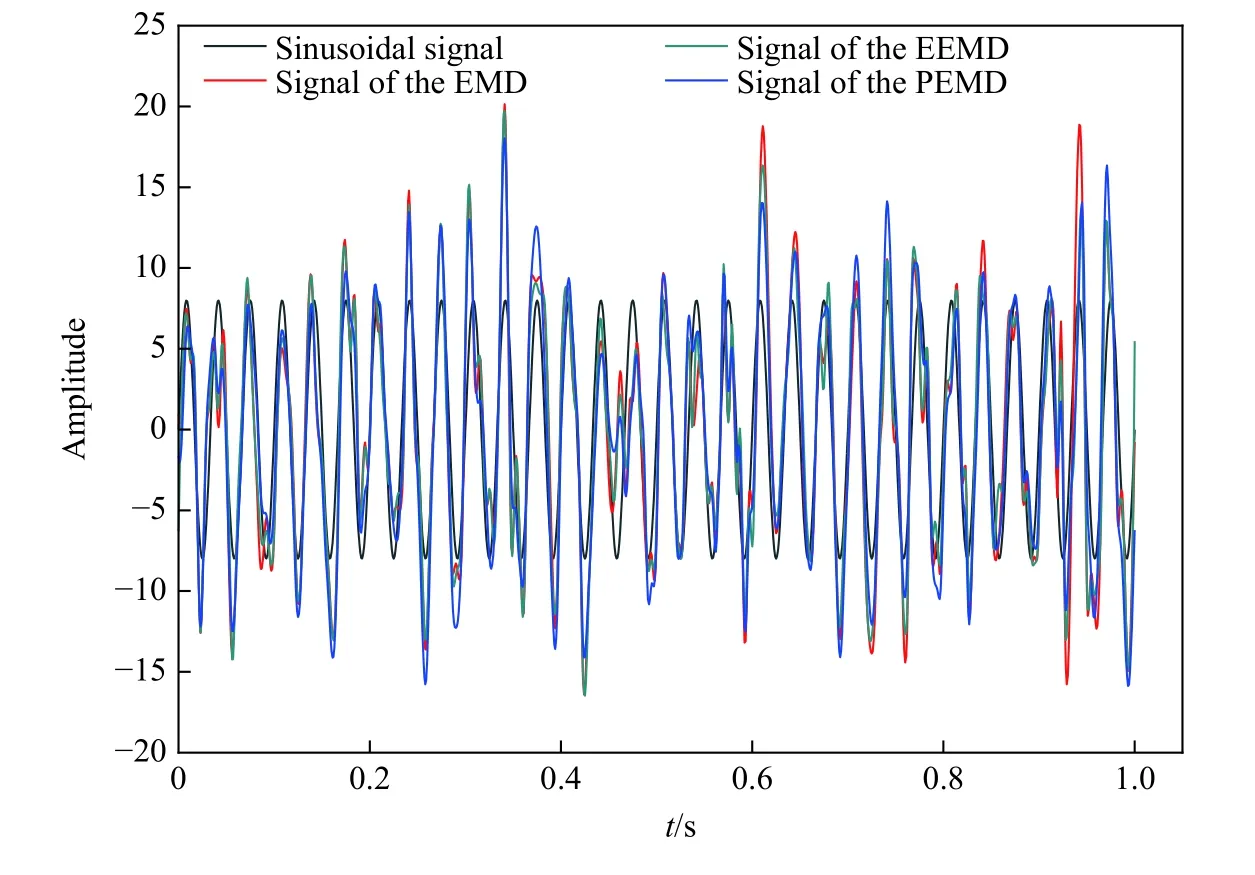
图5 EMD、EEMD 和PEMD 去噪信号时域对比Fig.5 Comparison of EMD, EEMD and PEMD de-noising signal time domain

表2 去噪效果评价指标Table 2 Evaluation index of de-noising effect

由表2 可知，改进算法相比于传统算法EMD 和EEMD，信噪比分别提高了1.15、0.38 dB，且均方根误差最低，因此从时域的角度分析PEMD 的去噪效果最佳。由于频率也是信号的一个重要特征，且噪声污染会直接对信号频率产生干扰，而短时傅里叶变换[17]能够将时域信号转化为频域信号，因此使用短时傅里叶变换进一步从频率的角度分析去噪效果，如图6 所示。

图6 EMD、EEMD 和PEMD 去噪信号频谱对比Fig.6 Comparison of EMD, EEMD and PEMD de-noising signal spectrum

由图6 可知，正弦仿真信号频率为30 Hz，三种去噪信号的主频均约30 Hz，达到了去噪的目的；为了对比三者的去噪效果，从各频率的能量进一步分析，如图6(a)所示，在峰值点30 Hz处，三者的能量均高于正弦仿真信号，但PEMD在30 Hz 处能量最大，故对正弦仿真信号频率(30 Hz)识别的灵敏度更高。

在0～160 Hz 的频带内，PEMD 的能量最接近正弦信号，对该范围内的噪声滤除效果最好；由图6(b)可知，在160 Hz 以上，PEMD、EMD 能量都比较接近正弦信号，但EMD 幅值低于正弦信号，发生了失真现象，因此PEMD 去噪效果最优。

3 爆破振动实验

实测爆破信号来源于江西省铅山县永平露天铜矿，爆破测振过程中设置5 个监测点,分别布置在东部边坡台阶不同高程上，其地质地形及监测点布置[18]如图7 所示。

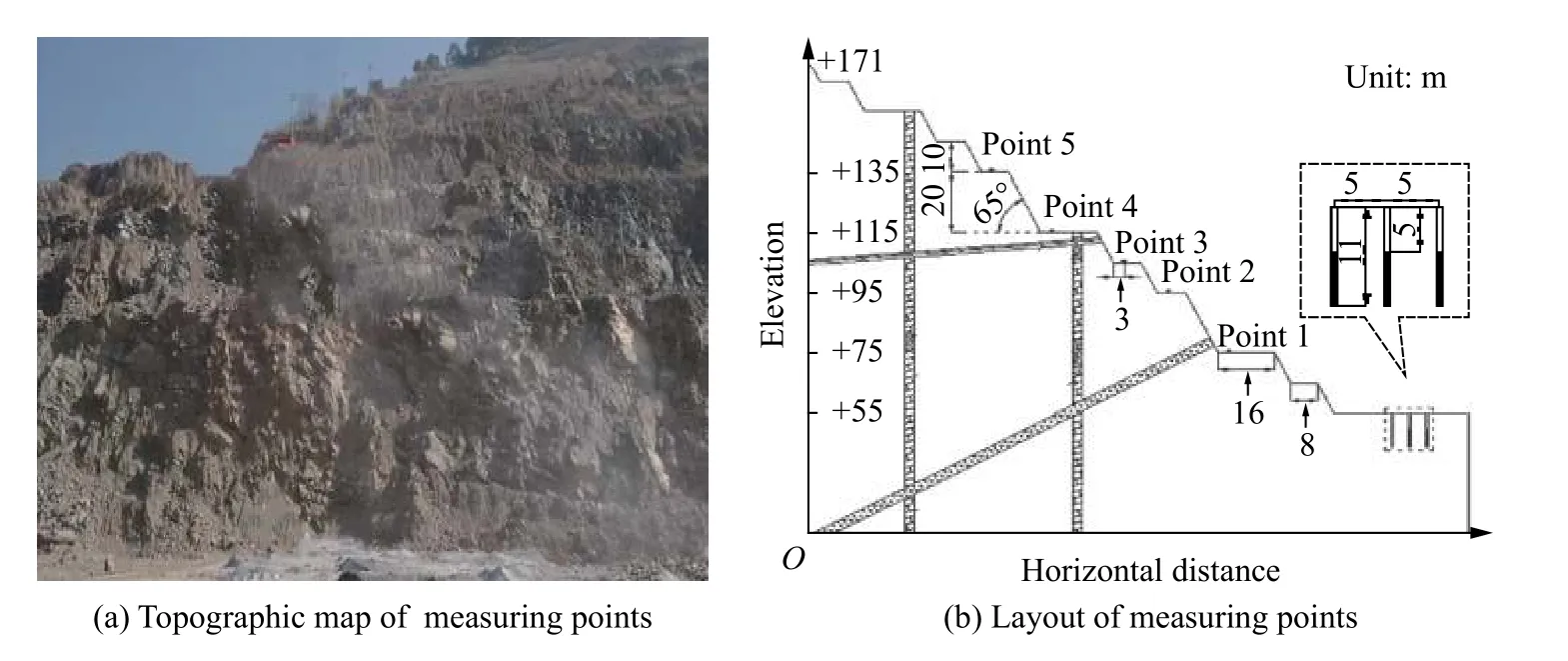
图7 地质地形及监测点布置图Fig.7 Geological topography and layout of the monitoring site

其中监测点具体参数见表3。

表3 不同测点的爆破参数Table 3 Blasting parameters of different measuring points

爆破过程中采用混装乳化炸药，炸药埋深8 m，装药密度1.1 g/cm3，炸药爆速3 200 m/s，炮孔孔深11.0 m、孔径200 mm、孔间距6.0 m、排距5.0 m、堵塞长度为5.0 m。根据测试条件的要求，本次测试信号的采样率设定为2 048 Hz，由于测振仪器采集到的爆破振动时域信号经常受到噪声污染，从而导致信号时域波形图产生大量噪声毛刺，对振动信号原始波形特性的识别产生较大影响，在此选取其中一组典型的爆破振动信号进行EMD、EEMD 以及PEMD 滤波去噪处理，分析三者的时域特征，如图8 所示。

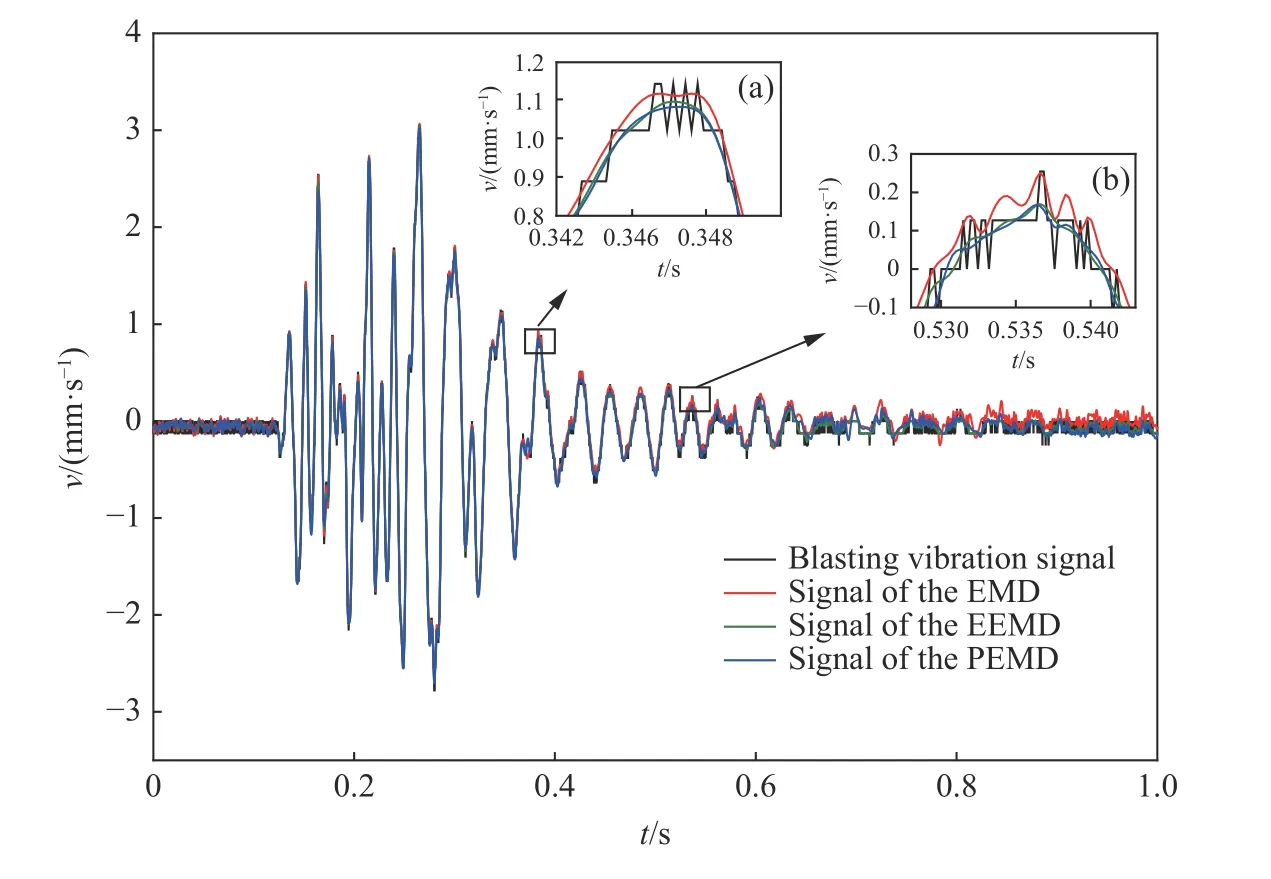
图8 EMD、EEMD 和PEMD 去噪信号时域对比Fig.8 Comparison of EMD, EEMD and PEMD de-noising signal time domain

由图8 可知，采集到的爆破振动信号在峰值点处不平滑，有很明显的噪声毛刺污染，三种去噪信号的峰值曲线趋于平滑，有效地消除了噪声毛刺，由图8(b)可知，PEMD 与EEMD 在峰值点处波动更少，且信号整体形态保留完整，在时域上去噪效果较为理想。

为了进一步比较两者的去噪效果，考虑到噪声会直接对振动信号的频率和能量产生很大的影响，因此使用短时傅里叶变换对两者的频谱进行对比分析，如图9 所示。

由于爆破振动信号主要集中在中低频，噪声集中在高频段，由图9(a)可知,在0～300 Hz 中低频范围内，PEMD 滤波信号的能量明显高于EEMD，对中低频振动信号能量保存效果较好。在高于300 Hz 的频带（图9(b)），随着频率的递增，PEMD 能量逐渐低于EEMD，滤除了更多的高频噪声。

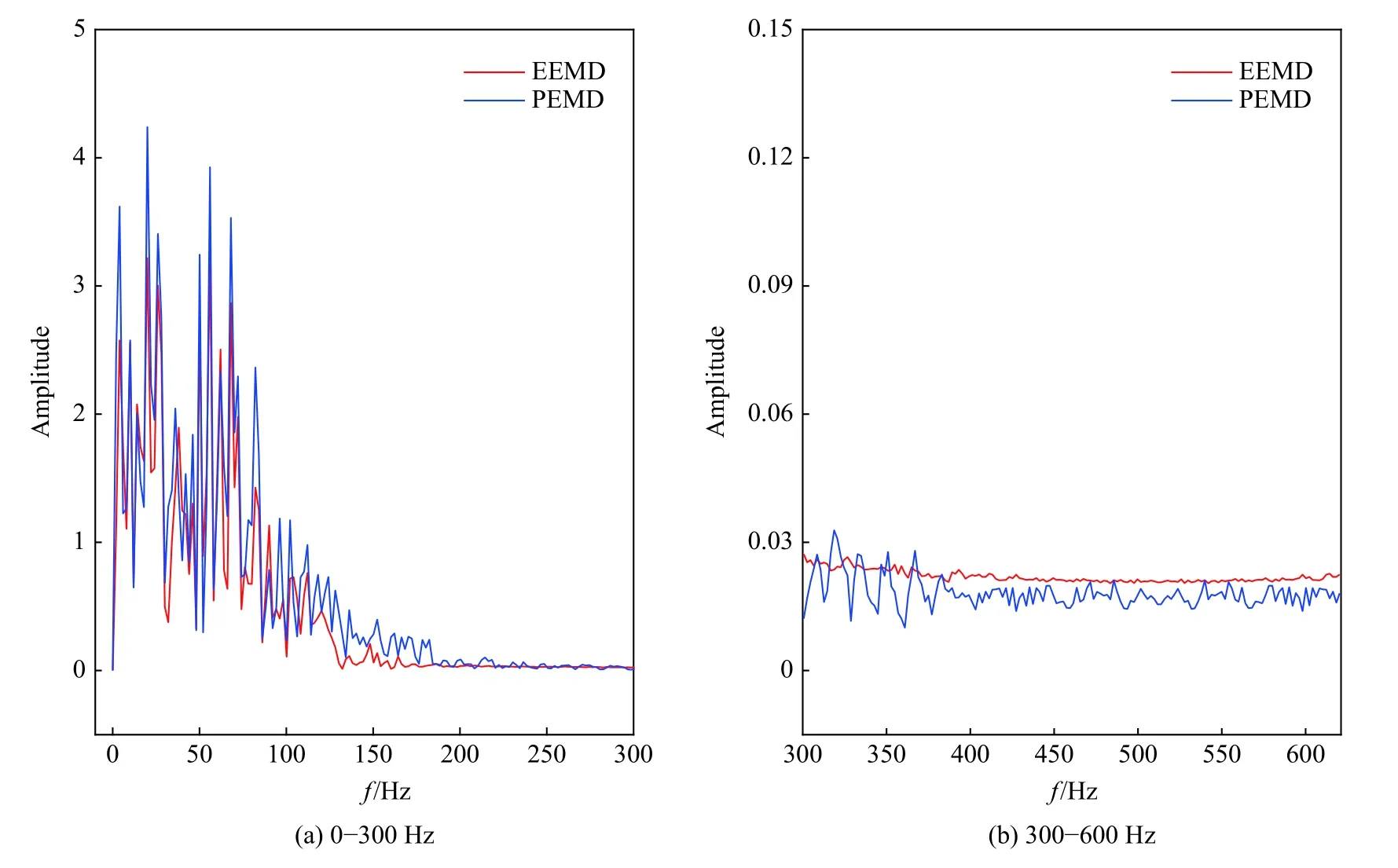
图9 EEMD 与PEMD 去噪信号频谱对比Fig.9 Comparison of EEMD and PEMD de-noising signal spectrum

4 讨 论

在实验过程中发现，同一信号EMD 分解出IMF 分量个数具有不稳定性，然而每一个IMF 筛分过程影响着分解结果的有效性和准确性，从而自然也会影响到后续的滤波效果，因此若筛分不完全，IMF 分量不能完整地表达原始信号的全部特性；筛分层数太多，则只能得到一些常量，没有实际物理意义[19]。因此Huang 等[20]设立了一种筛分评判依据即标准偏差系数作为EMD 分量终止标准，使得筛分次数有了一定的参考依据，但只有标准偏差系数的取值适当时，才能达到稳定的分解效果，因此该准则仍具有不稳定的收敛性。但此研究方法均是出于技术上对于EMD 算法添加限制进行改良，从而得到较为稳定的分解效果，而本文中PEMD 是从原始信号本身的特性出发，认为EMD 分解的不稳定性，表面上出于筛分终止条件的设定，实质是筛分过程中原始信号没有被完全正交分解，不同的信号一定程度上被随机分解到各个IMF 分量当中，导致每次分解结果出现不稳定性，从而出现模态混叠现象，而PEMD 在继承EMD 对信号自适应分解的基础上，严格地按照完全正交的原则对原始信号进行分解，具有不同特性的子信号均被一一剥离开来，因此每次分解得到的结果均是完全一致的，对比筛分准则依赖分解效果被动式选择参数的方法，PEMD 具有很大主动性和普适性，从而能很好地解决EMD 分解产生的模态混叠问题。

在解决了EMD 分解稳定性问题之后，接下来就是进行滤波去噪处理，因此需要考虑如何准确地判别有效的IMF 分量，Krishna 等[21]使用IMF 分量的抽取版本作为初始权向量，基于最大皮尔逊系数和最小峰度值对有效的IMF 分量进行选择；Chen 等[22]认为IMF 分量的个数由信号的长度而不是分解过程决定，导致分解后的IMFs 集中存在伪分量，进而对IMF 分量与一次噪声进行相关性分析，以消除伪分量的影响等。这些方法对于选择需要滤除的噪声分量和伪分量均有借鉴意义，但在本文实验中发现，仿真信号实验分解的IMF 分量过少，导致不论滤除哪些分量均不能达到很完美的去噪效果，因此不应仅仅局限于如何选择需要滤除的分量上面，而是应该从信号本身的特性出发，首先将信号完全正交分解，再结合自相关分析，通过比较自相关函数的特性曲线，即可筛选噪声分量，从而得到最佳的IMF 分量组合进行滤波去噪。

5 结 论

（1）利用PCA 结合EMD 的PEMD 算法，巧妙地融合了EMD 分解的自适应性和PCA 的完全正交性，是一种自适应性正交分解的信号去噪方法。

（2）PEMD 能够分解出完全正交的IMF 分量，解决了EMD 分解过程中出现的模态混叠问题。

（3）在仿真实验中，PEMD 相比于传统算法EMD 和EEMD，信噪比分别提高了1.15、0.38 dB 且均方根误差最低，去噪效果最佳；在正弦信号频率（30 Hz）处对仿真信号频率识别的灵敏度最高；在30 Hz 外的噪声频段对噪声的滤除效果最好。

（4）在爆破振动实验中，PEMD 和EEMD 去除噪声毛刺的效果较为理想，且PEMD 对0～300 Hz 中低频振动信号保存效果最好，300 Hz 以上高频噪声的滤除效果最好。

（5）本文仿真实验主要考虑高斯白噪声的影响，对于其他类型噪声的去噪效果有待进一步分析研究。