基于圆弧底试件的动态裂纹扩展及止裂规律研究*

郎 林，朱哲明，邓 帅，牛草原，万端莹，王 磊

（1. 四川大学深地科学与工程教育部重点实验室，四川 成都 610065；2. 四川大学建筑与环境学院，四川 成都 610065）

岩石和混凝土等脆性材料作为建筑材料，已在现代工程结构中得到广泛应用。虽然它们的基本力学性质已有大量研究和应用，但工程实践中，脆性材料常因其内部的微裂纹、孔洞、夹杂等缺陷导致结构出现宏观裂纹，严重时甚至导致隧道、桥梁、地下人防设施等重要工程结构损坏或完全失稳。因此，迫切需要开发裂纹止裂技术，防止工程结构中的已有裂纹继续扩展，尤其对某些重要工程结构[1-3]。

裂纹止裂技术先在金属材料中得到开发和应用，通常在裂纹尖端前部钻一个止裂孔来防止疲劳载荷下的静态裂纹萌生和扩展[4-6]。止裂孔的作用是使裂纹尖端变钝，减小裂纹尖端的应力集中[7-9]。为了研究爆炸荷载下圆形钻孔对运动裂纹扩展的影响，李萌等[10]在岩石试件的裂纹扩展路径上预先设置了两个圆孔，实验结果表明双圆孔对爆炸波引起的运动裂纹有抑制作用。杨仁树等[11]利用三点弯曲梁试件研究了Ⅰ型运动裂纹与圆孔缺陷的相互作用机理，结果表明圆孔对裂纹扩展速度和裂纹的应力强度因子有抑制作用。

对裂纹扩展行为和止裂规律有一些有意义的研究：张财贵等[12]用压缩单裂纹圆孔板试样(SCDC)研究了裂纹的萌生、扩展和止裂行为，指出裂纹止裂是一种突发现象；王蒙等[13-14]采用SCSC 试样、高速摄影系统和软件AUTODYN 研究了Ⅰ/Ⅱ型裂纹扩展特性，实验结果表明，裂纹扩展路径是弯曲的，在裂纹止裂处有明显的转折点；Gregoire 等[15]采用透明有机玻璃和高速摄像机进行了冲击实验，指出裂纹扩展过程中存在止裂和再起裂现象。这些研究说明脆性材料存在裂纹止裂现象，深入研究和合理设计，可以开发适合于脆性材料的裂纹止裂技术。

止裂现象发生是随机出现的，且摄影技术、应变片技术等现有测试技术仅对测试试样的一定区域进行监测，有可能监测的区域没有发生止裂而观测不到止裂现象。那么，就需要开发一种构型的试件使裂纹能够在监测区域出现止裂。为此，汪小梦等[16]、Lang 等[17]采用V 形底试样研究冲击加载下的裂纹止裂行为，试图通过改变试样的形状来发展在冲击荷载下的脆性材料裂纹止裂技术。其原理是，试件的V 形底部反射的压应力波抑制了运动裂纹，使裂纹停止继续扩展。对角度120°和150°的V 形底试件进行实验和数值模拟，结果表明两种试样对运动裂纹均有一定抑制作用。

另外，在断裂力学分析中，常采用临界动态应力强度因子描述动态荷载作用下裂纹的动态特征。在冲击载荷作用下，裂纹扩展过程中临界动态应力强度因子不是一个常数，它与裂纹扩展速度成反比[13-15,18]；而在爆炸荷载下，临界动态应力强度因子随时间频繁波动[11,19-21]。

为了进一步了解裂纹动态扩展及止裂规律，本文中设计一种带圆弧形底边的梯形开口边裂纹(trapezoidal opening crack with arc bottom，TOCAB)构型的试件。基于落锤加载实验装置和TOCAB 构型试件进行冲击实验，采用裂纹扩展计(crack propagation gauge，CPG)监测裂纹扩展时间并计算裂纹扩展速度。采用有限差分软件AUTODYN 对裂纹的萌生、扩展和止裂全过程进行数值模拟，结合实验和数值模拟对临界动态应力强度因子进行计算。通过实验和数值模拟，对裂纹的动态扩展行为和圆弧底部对裂纹的止裂机理进行分析探讨。

1 实 验

1.1 试件构型

在冲击实验中发现，SCDC 构型[12]、SCSC 构型[13-14]和SCT 构型[22]的试样在裂纹动态过程中存在止裂现象。为了进一步探究裂纹止裂机理和开发止裂技术，本文中设计了一种带圆弧形底边的梯形开口边裂纹(TOCAB)构型的试件，如图1(a)所示。在竖向冲击荷载作用下，TOCAB 试件弧形底部与透射杆之间会产生反射压缩波，在裂纹尖端前部形成的压缩应力水平分量减缓了运动裂纹的扩展，如图1(b)所示，最终导致裂纹停止扩展。

4 种TOCAB 试件的圆弧所对应的圆心角分别为0°、60°、90°和120°，如图2 所示。试件的宽度、高度和厚度均相同，分别为260、350 和30 mm；上部梯形开口宽度为80 mm，高度为100 mm；预制裂纹长度为100 mm、宽度为1.5 mm。120°的TOCAB 试件的几何尺寸如图1(a)所示，其底部圆弧的圆心角θ 为120°，所对应弦长为260 mm，预制裂缝起始于梯形开口底边中点且平行于试件中轴线，这是典型的Ⅰ型断裂裂纹。为保证裂纹从预制裂缝尖端有效起裂，实验前对裂纹尖端采用0.1 mm 薄钢锯条进行锐化处理。

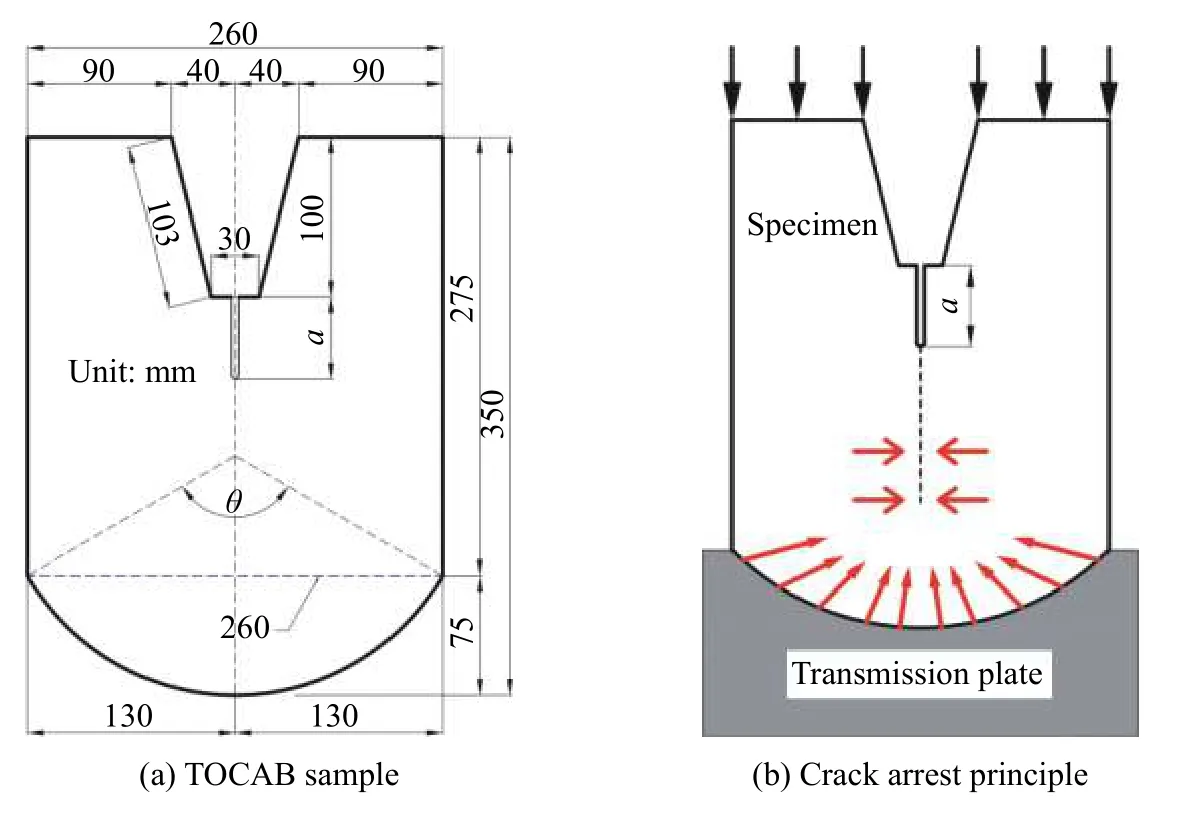
图1 试件几何尺寸和裂纹止裂机理Fig.1 Dimension of sample and crack arrest principle

图2 4 种用于研究动态断裂行为的大尺寸试件的构型Fig.2 Four samples were used to measure dynamic fracture toughness

1.2 材料准备和试件浇筑

以水泥粉煤灰砂浆作为模型材料，砂浆中各成分质量配比为：m(水泥)∶m(水)∶m(砂)∶m(粉煤灰)=1.000∶0.688∶3.013∶0.118。水泥为普通硅酸盐水泥P.O 42.5R，水为自来水，砂为本地河砂，粉煤灰为前锋电厂Ⅱ级粉煤灰。测试8 个边长15 cm、长度30 cm 的长方体试块和12 个边长10 cm 的立方体试块，其力学参数分别为：泊松比µ=0.22，弹性模量E=30.31 GPa，密度 ρ0=2 159 kg/m3，膨胀波波速cd=4 003.5 m/s，畸变波波速cs=2 398.6 m/s，瑞利波波速cR=2 187.9 m/s。

检测参数所用的试块和实验所用试件都在塑料模具中浇筑而成，在实验室常温环境下放置24 h 后，将试样取出并移入具有温度23 ℃和相对湿度95%的养护室中，直至达到需要的实验龄期，再取出进行实验。从同一批搅拌的砂浆中选材，浇筑了80 个构件，每种构型20 个。

1.3 落锤加载装置和CPG 测量技术

实验采用基于SHPB 实验原理设计的落锤冲击实验装置，如图3 所示，它由混凝土减震器、透射杆、砂浆试样、入射杆、波形整合器、冲击杆、红外线测速仪等组成。它的优点是入射杆和透射杆的尺寸比SHPB 杆大，可以对大尺寸的试件进行测试。为保证入射杆、透射杆与试件有良好接触并减少摩擦，实验前将试样上下端面打磨光滑、抹上凡士林润滑剂。实验时，将试样放置在入射杆与透射杆之间，并采用厚20 mm 的钢板夹住试件前后面，以防止试件屈曲，再将冲击杆从预设高度自由下落，采用红外线测速仪监测冲击速度。

如图3 所示，冲击加载装置的入射杆和透射杆都采用LY12CZ 铝合金材料，密度ρ1=2 800 kg/m3，泊松比µ1=0.3，弹性模量E1=71.8 GPa，铝合金杆的实测纵波波速为5 005 m/s。落锤采用钢铁，密度ρ2=7 850 kg/m3，泊松比µ2=0.25，弹性模量E2=205 GPa。安装在入射杆上端面的波形整合器采用紫铜材料。

在实验中，采用CPG(见图3)监测裂纹起裂和扩展到某处的时间。CPG 主要由间距相等的卡玛铜电阻丝并联布置于玻璃丝布基底上，再由两根主电阻丝连接至数据采集装置。CPG 长度和宽度分别为44 和18 mm，两根相邻电阻丝的间隔距离为2.2 mm。采用长35 mm 的灵敏电阻应变片记录入射杆和透射杆上的入射波、反射波和透射波。所有测试数据都通过超动态电阻应变仪收集，再由高精度、高增益、低漂移的放大器放大信号，以便高性能计算机记录保存。值得注意的是，CPG 测量线路中需要连接提供恒定电压的稳压源，所测量的电压信号才能被超动态应变仪读取收集，同样，电阻应变片测量线路中则需要连接集成了惠更斯电路的桥盒。

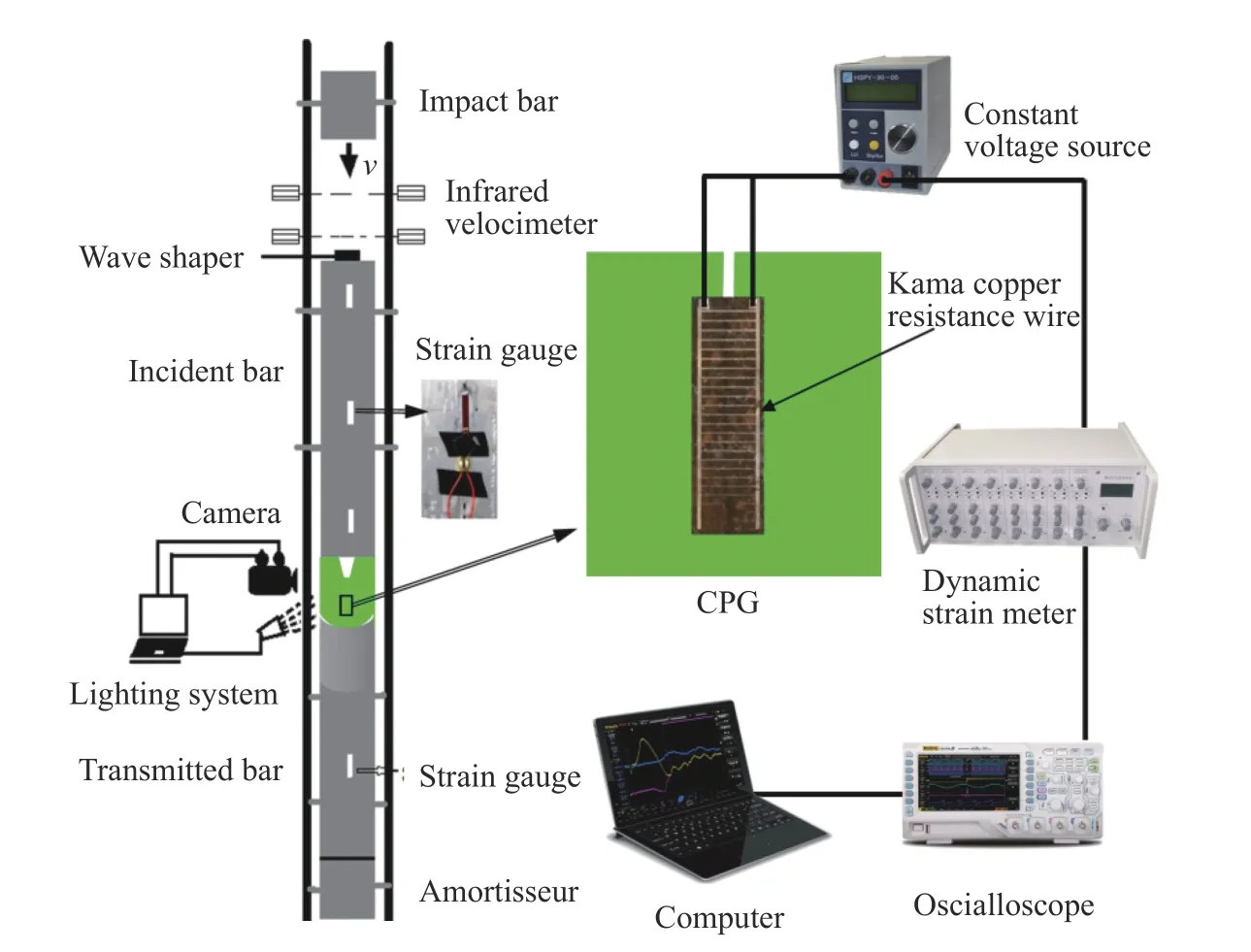
图3 落锤装置和数据采集系统Fig.3 Drop hammer device and data acquisition system

1.4 应变片和CPG 监测的数据

在实验中，在入射杆和透射杆中间点分别粘贴一个电阻应变片，监测实验过程中加载荷载。利用软件ORIGIN 对数字示波器采集的信号进行降噪处理，经计算得到相应的应变信号。试件上下端的动态荷载pi(t)和pt(t)为：

式中：下标i、r、t 和s 分别表示入射、反射、透射和试件，E 为杨氏模量，ε 为应变，A 为横截面面积。在冲击速度4 m/s 下，测试的荷载曲线如图4 所示。在随后的数值模拟中，将他们用作试件上的加载条件。动态荷载pi(t)随时间变化，其曲线弹性部分的斜率为加载率，可由软件ORIGIN 计算得到[23]。当冲击速度为4 m/s 时，其加载率为208.75 GPa/s。

将CPG 粘贴于裂纹扩展路径上，第1 根电阻丝与预制裂缝尖端对齐，以便监测裂纹起裂时刻。在竖向冲击荷载作用下，随着裂纹起裂，CPG 的电阻丝逐根断裂，超动态应变仪收集的电压信号呈台阶状跳跃。在加载率273.64 GPa/s的冲击荷载作用下，4 种TOCAB 试件的电压信号如图5 所示。将电压对时间求导，对应的极值时间即是电阻丝断裂时刻。由相邻两根电阻丝的间距2.2 mm 和其断裂时间间隔，可计算两根电阻丝之间的裂纹平均扩展速度。

由图5 可知，3 种圆弧底试件的裂纹在扩展过程中均存在延迟或止裂现象。对于60°的TOCAB 试件60-3，动态裂纹扩展至第4 根丝后停止了73.66 µs；对于90°的TOCAB 试件90-3，动态裂纹扩展至第15 根丝后停止了126.32 µs；对于120°的TOCAB 试件120-2，动态裂纹扩展至第20 根丝后停止了78.76 µs。图6 为3 种TOCAB 试件底部产生的反射压缩应力波的传播路径。对于60°的TOCAB 试样，反射压缩波能够传播到预制裂纹尖端，因此动态裂纹在扩展早期发生止裂。而对于120°的TOCAB 试件，反射压缩波能够传播到试件中部或下部，因此与60°和90°的TOCAB 试件相比，120°的TOCAB 试件的动态裂缝的止裂时间较晚。

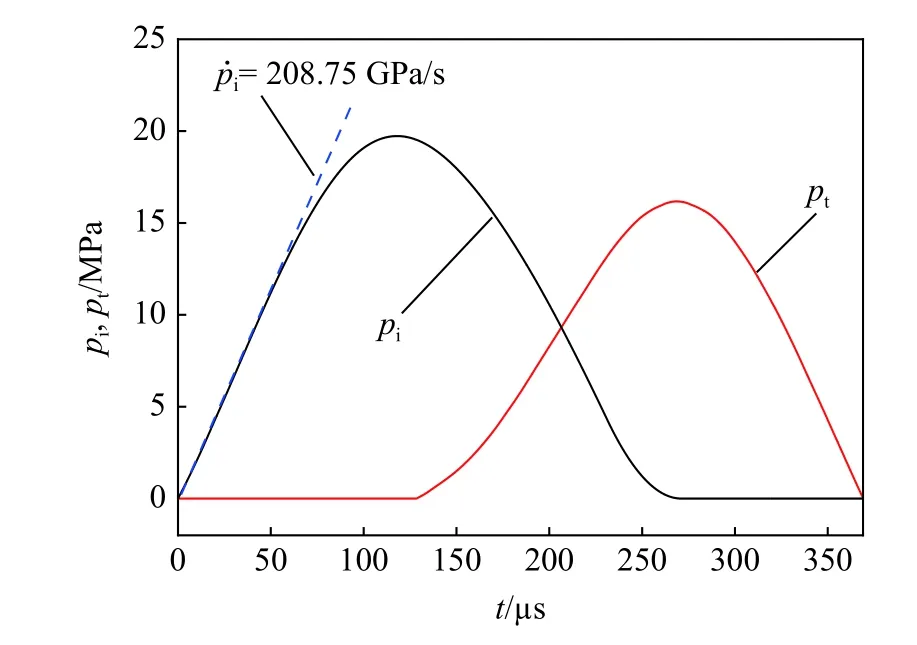
图4 由入射杆和透射杆测量的的荷载曲线Fig.4 Loading curves measured from incident bar and transmission bar

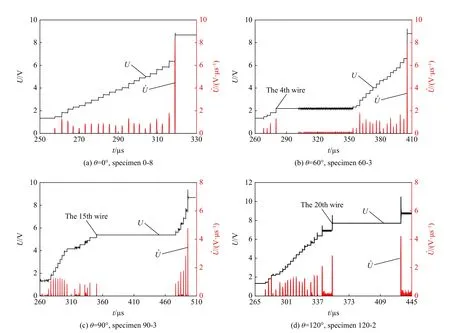
图5 电压信号及其对时间的导数Fig.5 Voltage signal history and its derivative with respect to time

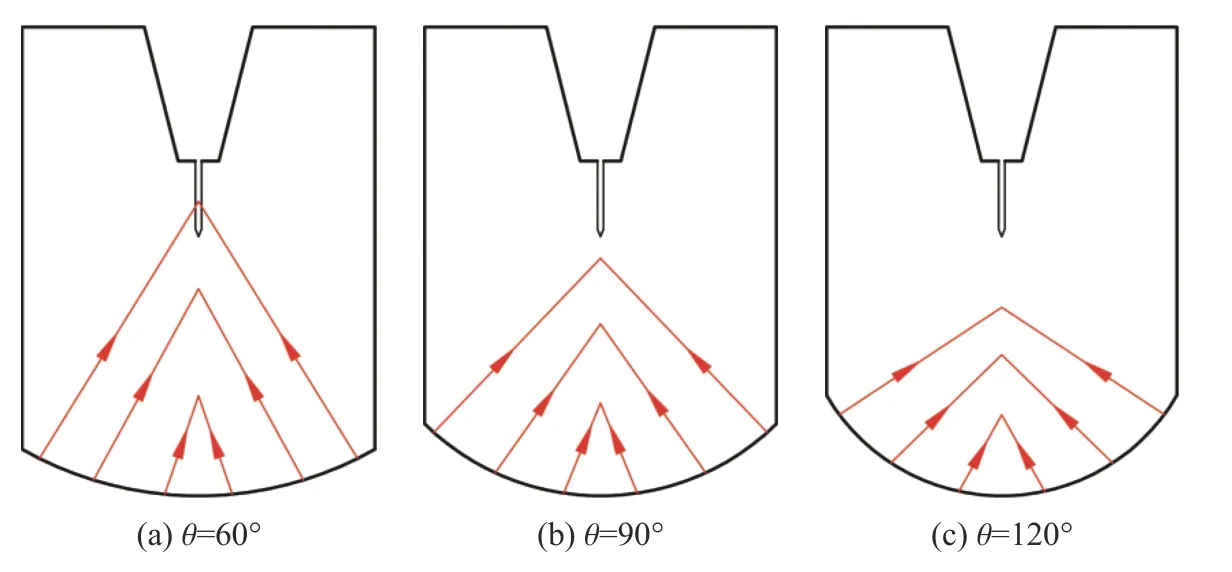
图6 圆弧底试件的反射压缩波Fig.6 Reflected compression wave of arc bottom specimen

1.5 裂纹扩展速度和裂纹尖端位置

相邻两根电阻丝的间隔距离除以两根丝断裂时间差，可得裂纹扩展速度。图7 为4 种TOCAB 试件在相同加载速率273.64 GPa/s 下裂纹尖端位移和裂缝扩展速度的测试结果。由图7 可见，裂纹尖端的位移随时间增加而增长，尤其在试件0-8(θ=0°)中几乎呈线性增加，在其他3 种圆弧底试件中各有一段平台，此时裂纹尖端停止扩展。裂纹扩展速度随时间波动，并不恒定。圆弧试件裂纹扩展速度的离散性比平底试件的大，裂纹扩展速度一般小于瑞利波波速的1/2。

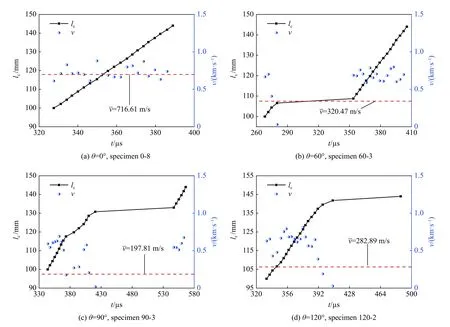
图7 裂纹尖端位置和裂纹扩展速度Fig.7 Crack tip locations and crack growth velocities

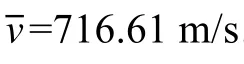
2 数值模拟

2.1 有限差分模型

为了进一步研究裂纹的动态扩展行为和裂纹止裂机理，采用有限差分软件AUTODYN 进行了数值模拟。软件AUTODYN 适用于冲击载荷作用下的脆性材料[13-14,16-17,22]。

在落锤冲击实验中，由于加载率较低，且材料的变形和压力较小，因此，将线性状态方程应用于砂浆材料。表示为：

式中：p 为压力， ρ0和 ρ 分别为材料的初始状态的密度和当前状态的密度，K 为体积模量。

Persson[24]提出了描述脆性材料宏观非弹性变形的累积损伤失效准则，累积损伤失效准则的有效性已被多位研究者证实[25-27]。在本文中，用累积损伤失效准则描述水泥粉煤灰砂浆材料的断裂行为，通过损伤因子D 描述材料的渐进性断裂，它与材料所经历的有效塑性应变相关。在软件AUTODYN[28]中，损伤因子为：

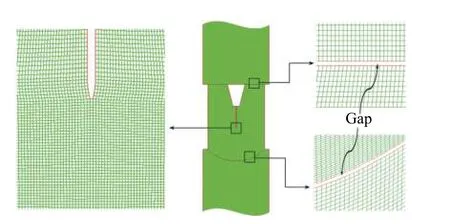
图8 落锤冲击装置和试件的网格划分Fig.8 Grid division diagram of drop hammer impact device and specimen

式中：εep为有效塑性应变，εep1为损伤因子为零时的有效塑性应变，εep2为损伤因子达到最大值时的有效塑性应变。

根据落锤冲击装置（见图3）和试件的几何尺寸，建立了二维有限差分数值模型，在模型中为了使相邻的两个构件之间有效传递应力波，设置了如图8 所示的间隙。在混凝土阻尼器的底部，设置一个透射边界，它可以将应力波传递到地面且没有反射。

采用四边形非结构网格，对落锤冲击加载系统进行网格划分。全局单元大小设置为1 mm×1 mm，对裂纹尖端区域和沿裂纹扩展路径上的单元网格进行加密，其尺寸为0.5 mm×0.5 mm，并将裂纹尖端设置成一个单元大小的平台，如图8 所示。试件划分单元网格总数为189 000 个，预制裂缝宽度为1.5 mm，裂缝长度为100 mm。

2.2 裂纹动态扩展特征

在加载率273.64 GPa/s 的冲击荷载作用下，对不同弧度的圆弧底试件进行了冲击实验和数值模拟。图9 为不同圆弧底试件的裂纹扩展路径的实验结果和数值模拟结果。可以看出，裂纹路径的数值计算结果与实验结果基本一致，但仍有轻微偏差，这可能由材料的不均匀性造成。θ=0°试件的裂纹扩展到了试件的底端，而其他3 种圆弧底试件，裂纹没有扩展到试件的底端，这表明，试件底部与透射杆之间产生的反射压缩应力波对运动裂纹起到了抑制作用。在其他3 种试件中，θ=90°试件的裂纹扩展长度最短，而θ=120°试件的裂纹扩展长度最长。

图9 裂纹扩展路径的实验结果和数值模拟结果Fig.9 Experimental results and numerical simulation results of crack growth paths

2.3 裂纹扩展路径上的水平压应力

为了进一步研究圆弧底试件的止裂机理，在裂纹扩展路径上设置了一组间距1 mm 的监测点，图10为裂纹路径上监测点分布和监测点的最大水平压应力。可以看出，圆弧底试件的最大水平压应力σx始终大于平底试件的最大水平压应力，这是因为，圆弧底与透射板相互作用产生的反射压缩波对裂纹路径上的监测点施加了额外的压力。在裂纹扩展的早期阶段，θ=60°试件的最大水平压应力σx略大于其他两种弧度的圆弧底试件，这是因为，θ=60°试件的反射压缩波能够到达预制裂缝尖端。然而，当裂纹扩展至试件中部后，即距离预制裂缝尖端约80 mm 后，在3 种圆弧底试件中，θ=120°试件的最大水平压应力σx最大，这也与图6 中对圆弧底试件的反射压应力的分析一致。

2.4 加载率对裂纹扩展长度的影响

图11 为4 种TOCAB 试件在不同加载荷载作用下的裂纹扩展长度。在加载率150～350 GPa/s 范围，3 种圆弧底试件的裂纹长度均小于平底试件的，随着加载率的增加裂纹扩展长度的增大较小。这说明，加载率对圆弧底试件裂纹扩展长度的影响较小，水平压应力对裂纹扩展的抑制作用显著。

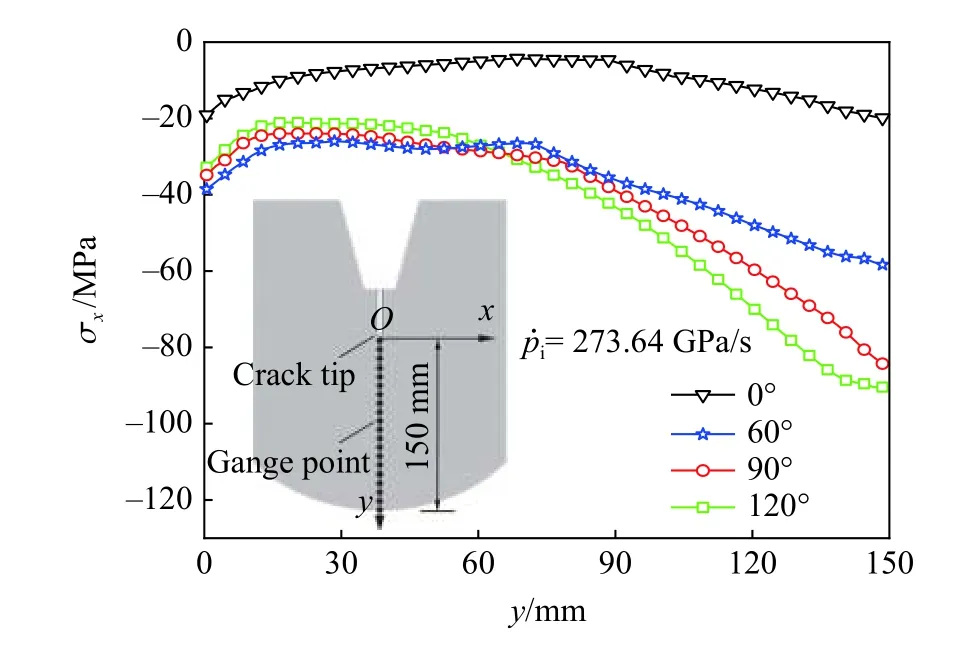
图10 试件最大水平压应力沿裂纹路径的变化Fig.10 Maximum horizontal compressive stresses along crack paths of specimens

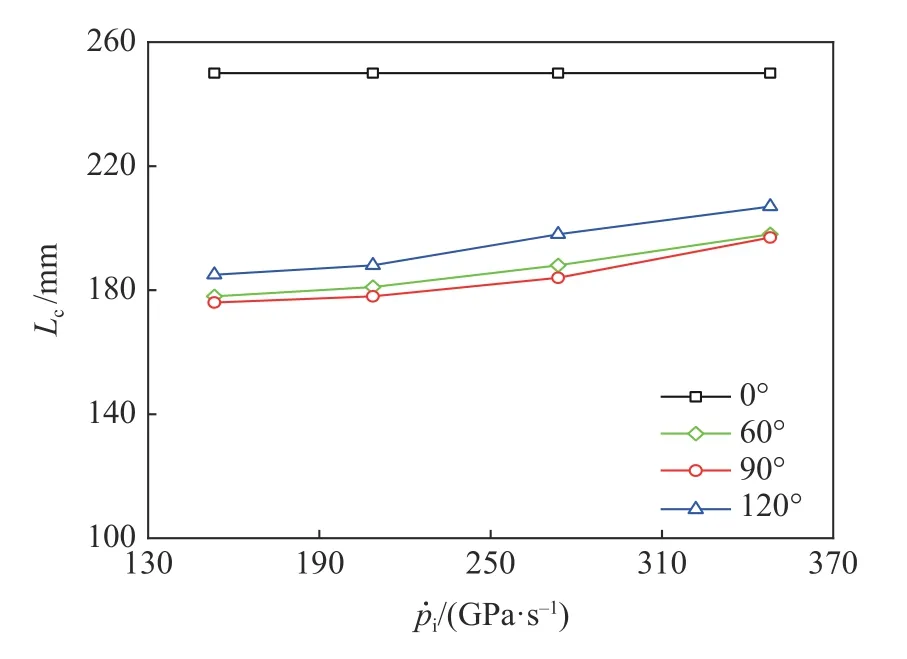
图11 裂纹长度随加载率的变化Fig.11 Crack lengths varying with loading rates

3 临界动态应力强度因子

在裂纹动态断裂研究中，除了研究裂纹动态扩展行为，还需计算裂纹的动态应力强度因子(dynamic stress intensity factor，DSIF)。DSIF 是描述裂纹动态扩展的一个重要断裂参数，通常不能直接测量到，而有限元软件ABAQUS 已经广泛应用于计算裂纹应力强度因子，因此采用实验-数值方法[13,16-17]计算裂纹扩展过程中的临界DSIF。为此，根据实验加载状况，建立了4 种TOCAB 试件的有限元数值模型。

3.1 ABAQUS 有限元模型

为了计算裂纹的DSIF，建立了落锤冲击加载下TOCAB 试件的有限元模型，如图12 所示。裂纹尖端附近区域采用1/4 三角形单元CPS6 进行离散化，其他区域采用四边形单元CPS8 进行网格划分。TOCAB 试件的网格单元数为12 303 个。水泥砂浆的材料参数见第1.2 节。在试件上下端分别施加动态荷载pi(t)和pt(t)，如图4 所示。

基于断裂力学理论[29]和位移外推法[30]，平面应变问题中的SIF 为：

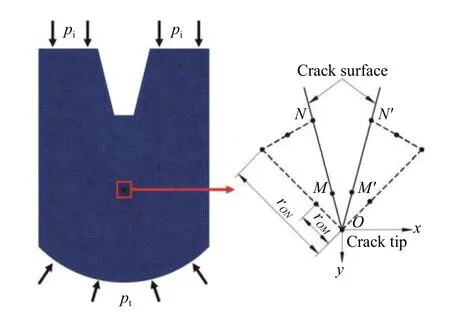
图12 有限元模型网格划分Fig.12 Finite element model meshing

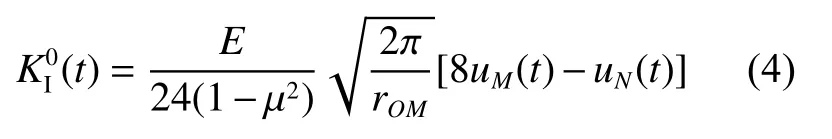
式中：E 和µ分别为杨氏模量和泊松比，u 为x 方向的位移，r 为半径；在一个单元中，rON为rOM的4 倍，如图12 所示。

动态荷载下的应力强度因子与静载荷下的应力强度因子是不同的，Freund 等[31]指出DSIF与裂纹速度有关：

式中：cR为瑞利波波速，cd为膨胀波波速。

3.2 临界DSIF 的确定

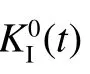
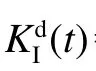
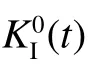
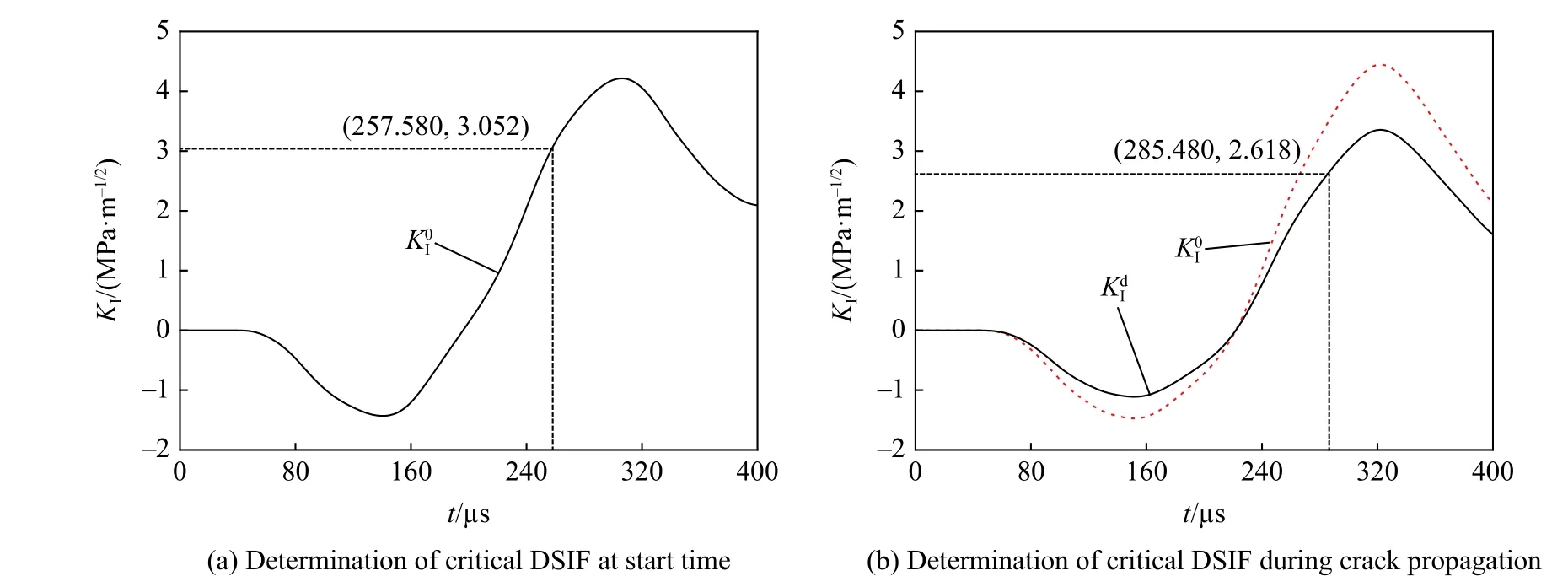
图13 在裂纹起始和扩展过程中临界DSIF 的计算方法Fig.13 Calculation method of critical DSIF during crack initiation and propagation

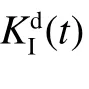
3.3 裂纹扩展中的临界DSIF

对于4 种不同弧度的TOCAB 试件，通过实验-数值法得到了每根电阻丝断裂处的临界DSIF。图14为4 种试件的临界DSIF、裂纹速度v 与瑞利波波速cR的比率随裂纹长度的变化关系。

由图14 容易看出，4 种试件在起裂和止裂时的临界DSIF 均高于扩展过程中的临界DSIF。这是因为，DSIF 随着裂纹扩展速度的增加而减小。由式(6)可知，当裂纹速度v 达到瑞利波波速时，DSIF 为零。在止裂点，即图14(b)中的第4 根丝、图14(c)中的第15 根丝和图14(d)中的第20 根丝，临界DSIF略大于裂纹起始点。这是因为，SIF 与裂纹长度有关，SIF 一般随裂纹长度的增加而增大，因此随着裂纹长度的增加，止裂时刻的DSIF 大于起始时刻的DSIF。

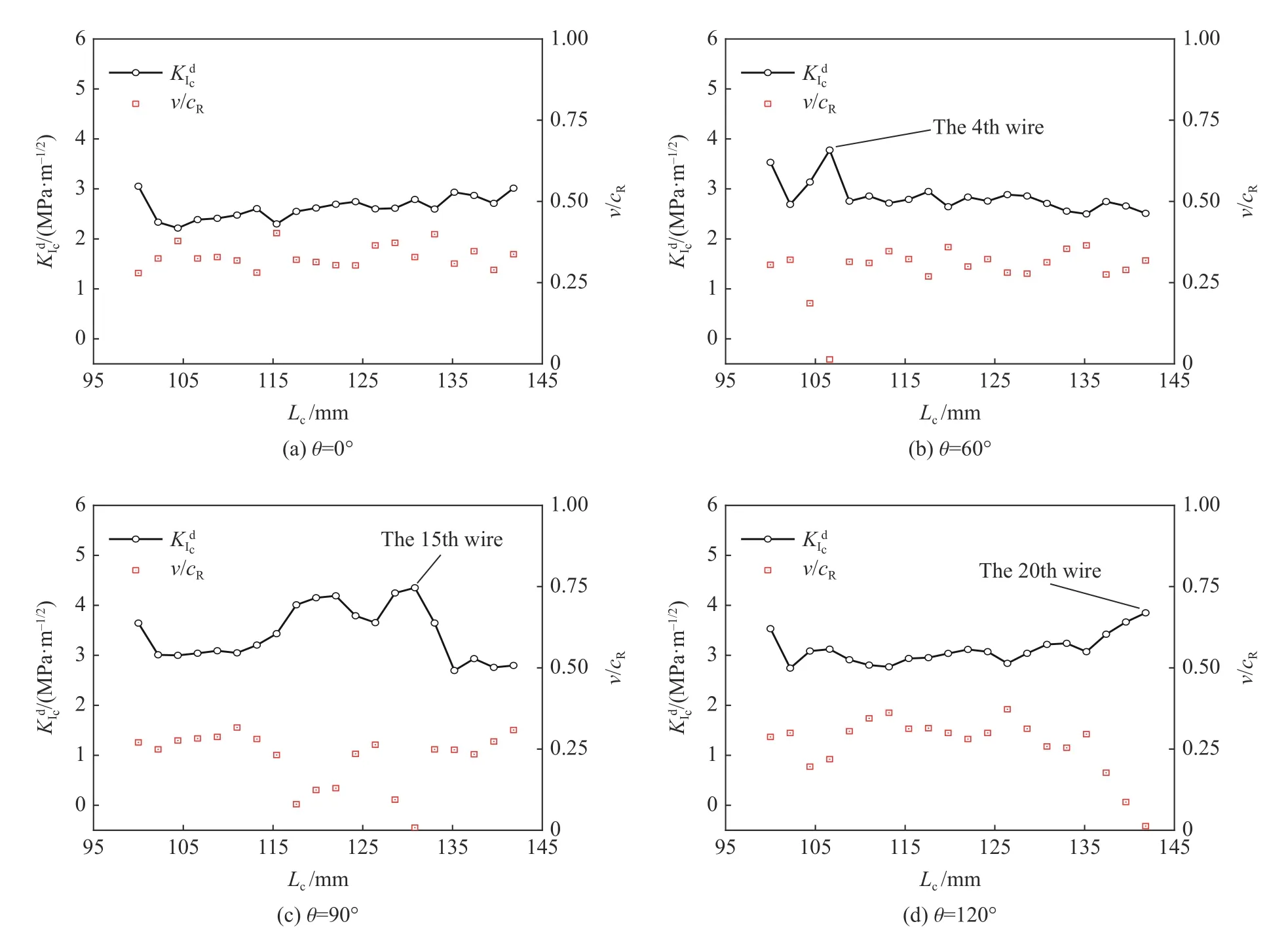
图14 临界动态应力强度因子、裂纹速度与瑞利波波速之比与裂纹长度的关系Fig.14 Critical dynamic stress intensity factors, ratios of crack velocity to Rayleigh wave velocity varying with crack lengths

4 结 论

（1）圆心角为60°、90°和120°的3 种圆弧底试件都可对运动裂纹止裂。其止裂机理为，从试件的圆弧底部产生的反射压缩波，在裂纹尖端前部形成的压缩应力水平分量抑制了运动裂纹的扩展。如需早期止裂可采用60°试件，如需后期止裂可采用120°试件。

（2）数值计算的裂纹扩展路径与实验结果基本一致，验证了数值模型的有效性。在150～350 GPa/s范围，加载率对裂纹扩展长度的影响较小，说明水平压应力对裂纹扩展的抑制作用显著。

（3）平底试件的平均裂纹扩展速度比圆弧底试件的大得多。在4 种TOCAB 试件中，90°试件的裂纹平均扩展速度最低。

（4）在起裂和止裂时的临界DSIF 均大于扩展过程中的临界DSIF，且由于应力强度因子随裂纹长度的增加而增大，因此在止裂时刻的临界应力强度因子高于起裂时的临界应力强度因子。