一种多无人机协同覆盖航迹规划算法∗

（火箭军工程大学 西安 710025）

1 引言

无人机具有成本低廉、无人员风险、隐蔽性强等优点，侦察、搜索及监控是无人机的主要应用领域，在历次战争中的出色表现证明了其在该领域的实用性[1]。无人机覆盖航迹规划是指在满足某些约束条件的前提下，为无人机规划出一条可以遍历目标区域的最优航迹[2]。研究多无人机的协同覆盖航迹规划问题对于提高无人机的侦察、搜索能力，强化其作战效能具有重要意义。

当前，国内外对于无人机覆盖航迹规划问题的研究主要基于机器人覆盖路径规划技术并进行拓展。Huang[3]等提出了基于图论生成的覆盖最优路径生成方法，并且研究出减少机器人转弯次数的方法，其中，最优路径是指能量消耗最小的路径。Maza[4]等提出了一种多无人机的近实时任务规划方法。该方法根据每架无人机的覆盖能力将目标区域分成多个子区域，使得每个子区域内只包含一架无人机。西工大的陈海[5]等提出了一种基于凸多边形区域的无人机覆盖航迹规划算法。该方法把覆盖航迹规划问题巧妙地转化为求凸多边形宽度问题，并且提出了一种凸多边形宽度的算法。无人机只要沿着垂直于宽度的方向飞行即可使无人机的转弯次数最少，从而保证覆盖飞行的时间和能耗等最小。

文章首先从动力学、无人机飞行时间和飞行路程的角度分析得出无人机的转弯过程是低效的结论，故将转弯次数的最小化作为航迹规划的优化指标。将目标区域分割为若干个子区域，要求每个子区域内有且仅有一架无人机，多无人机协同覆盖问题就简化为各子区域内的单无人机覆盖航迹规划问题。最后，对文献[5]提出来的无人机覆盖航迹规划算法进行改进，得到一种快速的覆盖航迹规划算法，最终实现了多无人机对目标区域的覆盖飞行。

2 覆盖策略的确定

无人机在转弯时受到最小转弯半径的限制，要实现完全覆盖整个目标区域，需要在目标区域外进行转弯飞行[6]。这一段转弯飞行相对于飞行任务来说是无意义的。因此，若能减少无人机覆盖飞行过程中的转弯次数，飞行的能耗、路程、时间等相应都会减少。

2.1 飞行能耗分析

下面，从动力学角度对无人机的转弯能耗进行分析。

为了方便问题的求解，做假设如下[7]。

1）在整个飞行过程中，无人机可看成质点。无人机的高度、姿态、以及传感器的角度不发生变化。

2）整个飞行过程中无人机状态稳定，且发动机推力方向与飞行速度方向一致。

3）目标区域的地形变化可忽略不计。且目标区域为凸多边形区域。

4）无人机的覆盖轨迹采用平行线的方式，即无人机沿直线飞行至边界后进行180°转弯，转弯方式如图1所示，而后沿反方向继续直线飞行，如此反复，直至目标区域被完全覆盖。

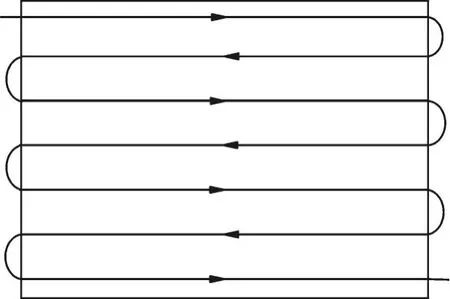
图1 无人机覆盖轨迹图

当无人机进行稳定的转弯飞行时，其飞行过程可视为在水平面内的匀速圆周运动。因此，在航迹坐标系内建立无人机的动力学方程如下[8]：

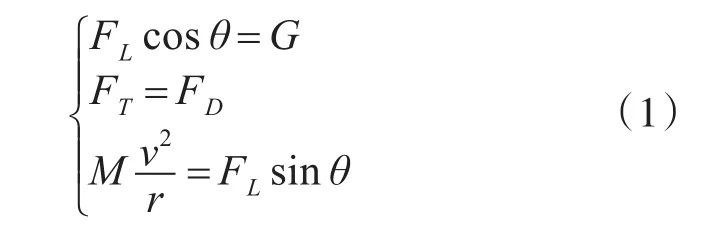
其中，M为无人机的质量，v是其飞行速度，FT是发动机推力，FD是飞行阻力，FL是升力，G是重力，r是转弯半径，θ是航迹滚转角。

无人机的法向过载n=FL/G，由式（1）可得n=FL/G=1/cosθ，且FL=G/cosθ。因为cosθ＜1，所以FL＞G。而无人机在正常沿直线平飞时FL=G。这说明无人机进行转弯飞行时的升力比沿直线平飞时的升力大。并可得到升力系数：

其中，CL是升力系数，ρ是当地空气密度，S是无人机机翼表面积。

综上，无人机在转弯飞行时的阻力为

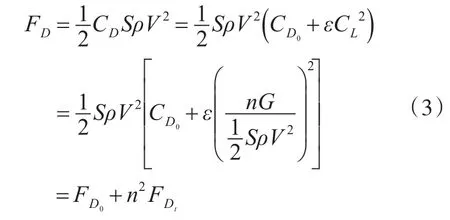
2.2 飞行路程与时间分析

当无人机的飞行姿态不发生变化时，传感器的探测范围可近似为一个等腰梯形[9]如图2所示。

无人机在转弯时受到最小转弯半径的限制，且无人机的地面投影与其传感器探测区域的中心不重和，要想完全探测到整个目标区域，无人机在每次转弯时，都需要在目标区域外多飞行一段圆弧的距离。因此，在进行航迹规划时，要尽可能减少转弯次数，从而缩短无人机的飞行路程，相应的也能缩短无人机的飞行时间。

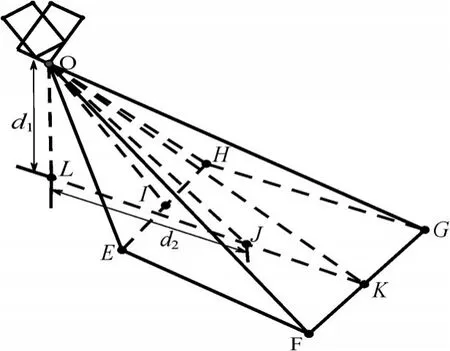
图2 无人机传感器探测区域图

综上，从飞行能耗、路程以及时间的角度分析，转弯过程是低效的。在进行航迹规划时，需尽可能减少转弯次数。因此，将转弯次数的最小化作为航迹规划的优化指标。

2.3 区域分割算法

假设目标区域为凸多边形，用Q表示，内有G架无人机执行覆盖任务。区域分割的目的是用G-1条线段将目标区域分割成G个子区域，每个子区域内有且仅有一架无人机。

在文献[10]中，在进行第一步分割后，得到的两部分区域分别包含G1和G2架无人机，但下一步如何分割并未涉及。为解决这个问题，本文借鉴广度搜索的思想，定义初值为D（Q）的队列，且其标志位为1。将每一次分割后，内部无人机数量大于1的多边形区域放入队列尾部，并将标志位相应后移，如此循环，直至每个子区域内有且仅有一架无人机，即可将目标区域分割成G部分。

利用上述方法对凸多边形区域进行分割，当改变初始顶点m1，其他顶点按顺时针依次排列时，分割结果将发生改变。因此，假设凸多边形顶点数为Q，则将其分割成两部分会有Q种结果。

假设使用Z架无人机对目标区域进行覆盖飞行，令每架无人机在各自负责的子区域内的转弯次数为yj。则Z架无人机的总转弯次数Y为

根据上文的论证，减少无人机的转弯次数是无人机航迹规划的主要优化指标。故在进行区域分割方案选择时，依次改变凸多边形的初始顶点，得到多种分割方案；而后，以所有无人机的总转弯次数为依据，在所有分割方案中选择Y值最小的方案。

3 基于距离比较的覆盖航迹规划算法[4]

单个无人机在各自的目标区域内的总飞行路程可以由Sin和Sout两部分来表示。其中，Sin表示无人机在目标区域内部的飞行路程，Sout表示无人机在目标区域外部的飞行路程。因为无人机是不重复地对目标区域进行覆盖飞行，所以有

转弯次数的表达式如下：

其中，K为凸多边形区域的宽度。

凸多边形的跨度和宽度的定义：在平面内取两条距离足够远的平行线，让两条平行线向其中心平移直至与凸多边形相交，此时两平行线的距离即为凸多边形的跨度，所有跨度中的最小值就定义为凸多边形的宽度。另外，证明了凸多边形的每条边都对应一个跨度，宽度只会出现在“点边式”跨度中；且无人机在凸多边形区域内飞行时，最少转弯次数的飞行方向肯定与该区域的一条边平行[5]。

根据式（6）可知，只要求出凸多边形区域的宽度，就能得到无人机飞行时的最少转弯次数。因此，无人机的覆盖航迹规划问题就转化为求凸多边形区域的宽度问题。

基于上述思想，在文献[5]中，作者提出了一种凸多边形区域的覆盖航迹规划算法。该算法的基本思路：第一步，求出凸多边形任意一条边上除去该边上两个顶点外的所有顶点与该边的距离；第二步，比较出所有距离里面的最大值，即为相应边的跨度；第三步，逐次计算出每条边的跨度；第四步，对每条边的跨度进行比较，其中的最小值即为凸多边形的宽度；最后，在航迹规划时，让无人机的飞行方向平行于凸多边形的宽度所对应的边，从而保证转弯次数最少。基于上述思想，凸多边形的宽度算法如下。

设凸多边形的顺时针顶点序列为{m1,m2,…,mn+1} ，n为顶点数（n不小于3），顶点mi的坐标是(xi,yi)，且(xi+n,yi+n)=(xi,yi)

输入凸多边形的顺时针顶点序列，顶点mi的坐标是(xi,yi)，(xi+n,yi+n)=(xi,yi)。

输出宽度K及其对应的边和顶点序号，分别用Lk和Tk表示。

Step 1令i=1,j=1

Step 2ifj≠i且j≠i+1（不用考虑边mimi+1上的两个顶点），按式（7）可求出点mj到边mimi+1的距离平方：

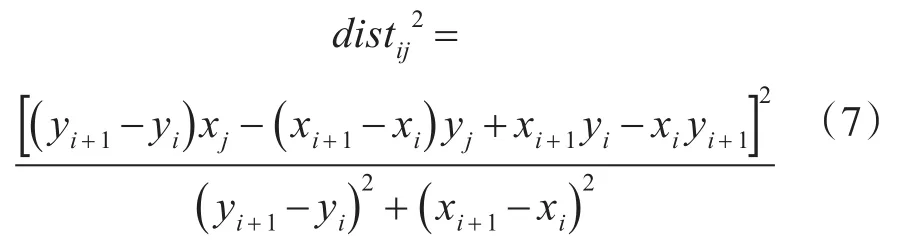
Step 3ifj=n，则执行Step 4，否则令j=j+1 ，执行Step 2；

Step 4依次求出与边mimi+1对应的n-2个，并求出其中的最大值distij-max2以及其对应的顶点序号Di-max；

Step 5ifi=n，执行Step 6，否则令i=i+1，执行Step 2；

Step 6找出所有distij-max2中的最小值并进行开方处理即可得到该凸多边形的宽度K，其对应的边和顶点序号记为Lk和Tk。

通过计算可知，对于凸n边形区域，该算法每次循环需进行16次四则运算，总共需要循环n（n-2）次。所以，该算法总共需要进行16n（n-2）次运算，故其时间复杂度为o(n2)。

4 一种快速的无人机覆盖航迹规划算法

本文在基于距离比较的覆盖航迹规划算法的基础上进行改进，提出了一种快速的凸多边形宽度求解算法，从而得到相应的快速覆盖航迹规划算法。

根据凸多边形的性质，可得以下结论：边mimi+1跨度相应的顶点是mg，其按顺时针方向的邻边mi+1mi+2上跨度相应的顶点必定是mg或者其沿顺时针方向之后的点[11]。

在第3节所提航迹规划算法的第一步中，需要依次求出每条边与若干点的距离，并找到其中的最大值，即为相应边的跨度。然而，距离计算公式较为复杂，当凸多边形的顶点数量较多时，计算量十分巨大。

其实，只需要找到点边距离中的最大值，而没有必要求出每个点边距离的具体数值。结合这一思想，本文提出了快速航迹规划算法。

算法的基本思路为第一步，求出凸多边形每条边的直线方程；第二步，任意取一条边为起始边，在该边所对应的直线方程后加一个常数C，将除去该边上两个顶点外的顶点坐标依次代入新的直线方程求出常数C，并将相邻两顶点所求出的C的绝对值进行比较得到Δ（前顶点减后顶点），直至Δ≥0为止。此时，即可找到距离该边最远的点，从而得到相应边的跨度；第三步，依次将上一条边跨度对应的点及其以后的点代入下一条边的直线方程中，并按照第二步中的方法求出Δ，直至Δ≥0为止。如此循环，直到所有边的跨度求出为止，最后再找出其中的最小值即为该凸多边形的宽度。

由上文可知，顶点mi的坐标是(xi,yi)因此，凸多边形的第i条边的直线方程可用下式表示：

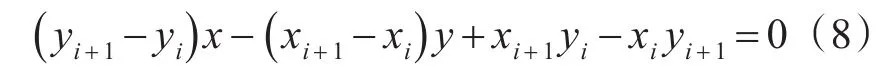
输入凸多边形的顺时针顶点序列，顶点mi的坐标是(xi,yi)，且(xi+n,yi+n)=(xi,yi)，空数组R，C，Δ。按照式（8），分别求出凸多边形每条边的直线方程。

输出宽度K及其对应的边和顶点序号，分别用Lk和Tk表示。

Step 1：令i=1,j=i+2；

Step 2：按照下式求出Δ：

Step 3：if Δ≤0，根据距离式（7），求出dist2ij-max，且令V=j,Ri=j,i=i+1，并执行Step 4，否则令j=j+1，执行Step 2；

Step 4：ifi≥n+1，则执行 Step 7；否则，令j=V；

Step 5：按式（9）求出Δ；

Step 6：ifΔ≤0，根据距离式（7），求出dist2ij-max，且令i=i+1,V=j执行 Step 4，否则令j=j+1，执行Step 5；

Step 7：找出所有dist2ij-max中的最小值开平方根即为所求宽度，其对应的i,j即为凸多边形宽度所对应的边和顶点的序号，分别用Tk和Lk表示。

5 仿真分析

对于目标区域为凸多边形的多无人机协同覆盖航迹规划问题，首先需要利用凸多边形分割算法把目标区域分割成若干个子区域。而后分别找出每个子区域的宽度所对应的边和顶点，从而确定无人机的飞行方向，最后采用平行线的覆盖方式对目标区域进行覆盖飞行，即可实现覆盖航迹的转弯次数最少。

现有凸多边形区域如图3所示，安排四架无人机对其执行覆盖任务，其顶点按顺时针排列依次为{v1,v2,v3,v4,v5,v6,v7}，其对应的坐标依次为

利用Matlab软件编程进行仿真，结果如图3所示。

图3 目标区域图

采用2.3节中的区域分割算法可将目标区域分割为四部分，如图4所示。

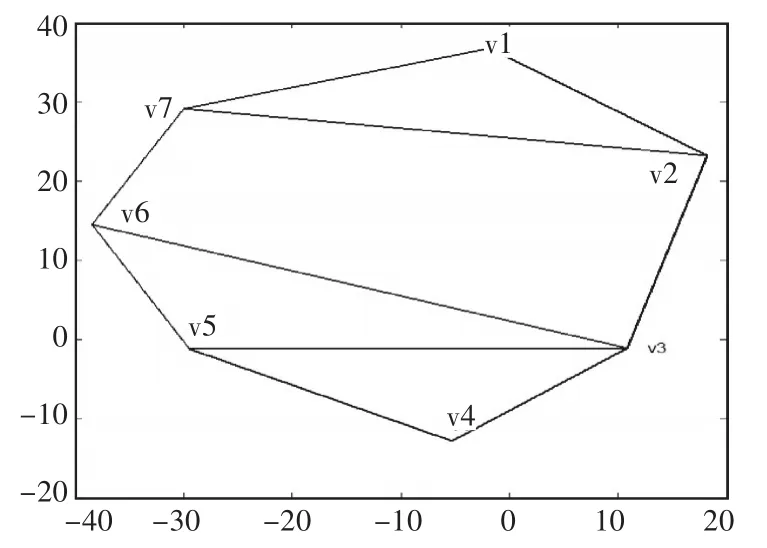
图4 区域分割图

在仿真过程中，采用栅格法[12]建立目标区域的环境模型。当某个栅格单元中包含部分目标区域时，也认为该单元是需要进行覆盖的。且假设无人机探测器扫描宽度的一半等于无人机的转弯半径。最终得到目标区域的多无人机覆盖航迹规划结果如图5所示。

图5 多无人机航迹规划图

仿真结果表明，本文提出的快速覆盖航迹规划算法可以较好地实现多无人机的协同覆盖航迹规划，优化了算法的计算效率，降低了算法复杂度。算法主要围绕多边形区域的边和顶点进行循环迭代求解。在整个求解过程中，所有的边只遍历一次，顶点的遍历次数在最差的情况下也不会超过两次。因此，算法可以在线性次运算内求得凸多边形的宽度，从而完成对无人机的航迹规划，其算法复杂度为o(n)。

为了更好地对两种算法的运行效率进行比较，对两种算法均进行100000次宽度计算，其运行时间如表1所示。

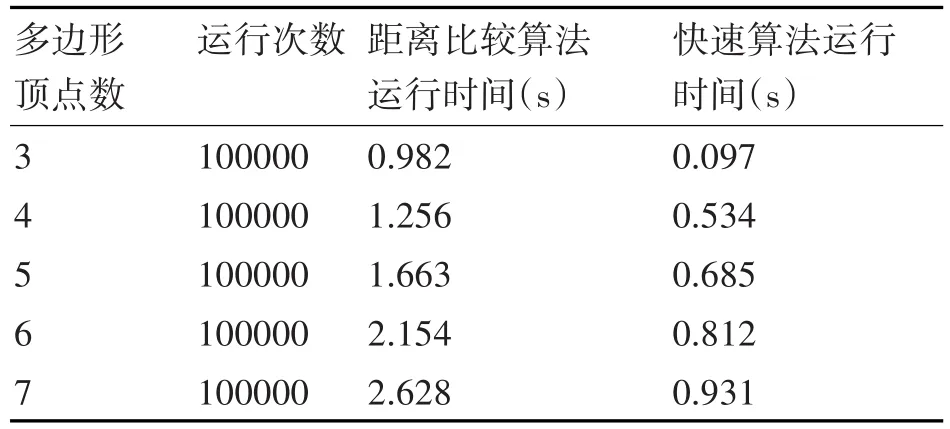
表1 算法运行时间仿真结果

由表1可知，快速航迹规划算法在运行效率上较基于距离比较的航迹规划算法有较为明显的改进，对于增强无人机的覆盖能力具有一定的指导意义。

6 结语

主要对现有的无人机覆盖航迹规划算法进行改进，得到一种快速的覆盖航迹规划算法。通过仿真实验，验证了该算法的可行性，证明了该算法的运行效率较原算法有较为明显的提升。

但是，本文改进的多无人机协同覆盖航迹规划算法仍然存在一些不足。首先，没有考虑更一般的非凸多边形区域；其次，忽视了障碍物以及目标区域地形变化的影响；最后，忽视了无人机传感器扫描宽度与其转弯半径的对比关系对无人机转弯方式的影响。以后，将对凹多边形区域的凸分解、三维覆盖航迹规划及无人机转弯方式等问题进行重点研究，完善多无人机协同覆盖航迹规划算法。