“两点一线”初中数学小专题教学策略研究

陈凰

【摘要】当前的初中数学教学状况不甚理想，数学复习课中也普遍存在着“以练代讲”的情况，导致复习课堂十分枯燥，教学效果不明显，学生的数学核心素养也得不到良好的发展。为了解决低效复习的现状，尝试采取小专题教学策略。笔者在长期的教学实践以及理论钻研中，提出了“两点一线”的小专题教学模式，并申请了梅州市市级课题进一步研究，希望通过本论文的探讨与分析，能够为初中数学教学工作者带来一些启发。

【关键词】两点一线   初中数学   小专题教学   策略

初中数学复习课堂普遍存在着问题主线不清楚、学生参与度不高，数学思想方法提炼不够等问题。如何解决这些问题是摆在我们数学教师面前的重要任务。2018年9月至今，我们教研组尝试进行了36节“两点一线”的小专题复习课，深受学生们的欢迎与喜爱，取得了良好的效果。

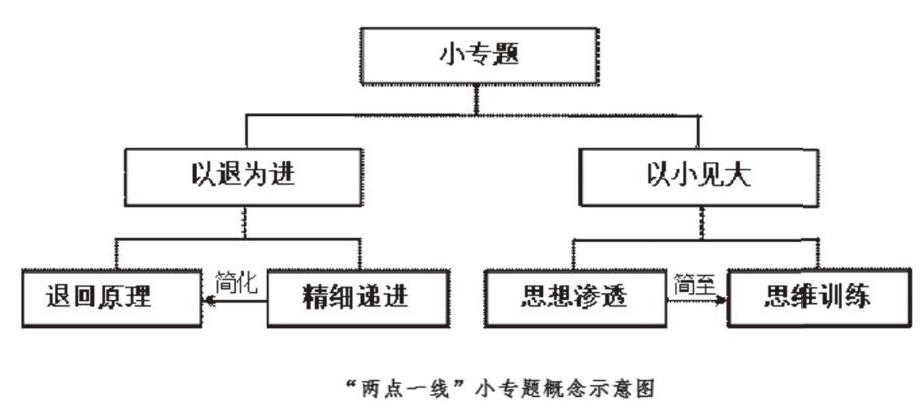
一、“两点一线”小专题的概念界定

“两点一线”小专题教学：以解决一道中等题目为主基调，先让学生“退”到解决题目的基本概念或者原理进行回归性学习，再用一条清晰的主线来串联这些概念和原理，“进”到原题中解决问题，即“以退为进”;在设计上，要求简化原题，通过设计学生最近发展区内的简单题目，以突出核心知识，提高思维训练，即“以小见大”。

二、“两点一线”初中数学小专题教学策略

下面以《小专题：一元二次方程根的判别式的应用》复习课为例进行阐述。

1.退回原理，唤起知识

在传统的初中数学教学模式当中，尤其是在复习的过程中，教师对概念和原理就很少侧重，更加倾向于让学生做大量的数学题来巩固提高。教师认为学生的问题是在于不会做一些复杂的题目，实际上这是因为学生的基础知识没有打牢，尤其是一些小的概念和数学原理。因此教师应该要重视知识结构与体系，以基础的知识点来展开教学，唤醒学生的记忆，从而为学生做一些复杂的数学题打下基础。

为了让学生了解一元二次方程根的个数基本分类，我先设计了几道方程题，从最基本的原理入手，让学生充分的自我探究。具体实施如下：首先将班内学生分成了三组，让学生分别就（1）X2+2X=8;（2）X2-X=0;（3）X2-X=-2进行探究，最后分别得出（1）X=2，X=-4;（2）X=±1;（3）无实根。学生探究得出三个方程的根都不相同。此时我提出问题，退回原理，让学生就方程的根为何不一样再进行探究，思考是否还存在其他情况。从基础的知识点来展开复习，让学生能够深刻领悟一元二次方程根的判别式相关概念，感悟基本原理的作用。

2.设计问题，精细递进

问题是思考的基础，也是学习的开始。古代孔子就十分注重利用问题来启发学生，苏格拉底也曾发明了“产婆术”的教学方法，主张给学生创造问题情境。“两点一线”的小专题教学模式注重设计问题串启发学生思考探究，让学生在解决问题的过程中享受到碰撞思维的乐趣。教师通过设计层层递进的问题，在学生认知特点和学习能力的基础上设计层次性的问题，让学生逐步地得到提高。

例如，在复习一元二次方程的判别式后，以问题的形式实施了精细递进。关于x的一元二次方程kx2-2x-1=0

（1）若方程有两个相等的实数根，则k取值范围是_______。

（2）若方程有实数根，则k取值范围是_______。

（3）若方程没有实数根，则k取值范围是_______。

让学生在由浅入深的思考过程中进行归纳总结，要求待定系数的取值范围则通过判别式来进行计算，通过递进的问题增强学生思考解题的能力。

3.总结提炼，思想渗透

在课程改革的背景之下，要充分发挥数学思想的重要性。数学思想是解决数学问题的一个有力武器，同时也是数学核心素养的重要组成部分。小专题教学讲究数学练习题的质量，让学生在做题的过程中总结数学思想方法，这样能以小见大，因为即便是在复杂的数学问题，只要掌握了数学思想方法，也就很容易解决。

例如，在总结本节课时，随机找学生谈一谈自己在本节课有哪些收获？这样学生会自己主动思考总结知识点，围绕本节课的复习内容（1）一元二次方程根的判别式的意义;（2）由根的判别式的符号判断一元二次方程根的情况等主题进行回答，对于一些知识点误区教师进行适当点拨。最后教师再特别强调一下本节课要掌握分類讨论思想、数形结合思想等，从而达到自己的预期教学效果。

4.题型巩固，思维训练

相比于数学思想方法，对于学生来说数学思维能力可能更加抽象化。数学思维能力是包括思维的敏捷性、灵活性、批判性、广阔性、深刻性等，教师应该借助一些典型的题型，来帮助学生进行思维训练。例如，不解方程式，只需用b2-4ac的值>0、<0、=0的情况判定方程根的情况。如：（1） 12x+x2=3，（2）6x2+2x+1=0，（3）4x2-x+8=0，（4） x2-7x-18=0。通过题型巩固来使学生判别方程是否有实根和两个实根是否相等，弄懂为什么可以用判别式判别一元二次方程根的情况。

总而言之，在初中数学教学中进行“两点一线”小专题教学，不仅能够改变传统的复习课堂模式，也能够激发学生的数学思维，同时对促进教师的专业素养也有着重要的意义。

【参考文献】

[1]沈岳夫.知识与能力并重 思想与经验齐驱——初中数学专题复习“组块式”教学模式初探[J].中学数学杂志，2013（10）：17-19.

[2]王芸，韩龙淑.PCK视角下的初中数学专题复习课解析——以概率专题复习课为例[J].中国数学教育，2019（Z3）：42-45.