基于GA-BP的大坝渗透系数多目标反演分析方法

唐少龙，熊 威，万小强，罗梓茗，万思源，汪 庆

(江西省水利科学研究院，南昌 330029)

在水利工程渗流分析中，渗透系数的合理取值对工程渗流场的分布及渗透稳定评价至关重要。传统渗透系数获取方法主要通过钻孔压水试验，由于受工程运行时间及人类活动等的影响，工程渗透系数在正常运行管理过程中会发生一定的变化[1,2]，无法适时掌握其变化情况。根据工程运行监测数据进行渗透系数反演成为当前重要途径，其能够经济、快速的获取实际渗透系数情况。

由于在大坝渗流过程中参数与效应量之间具有较强非线性特性，在对大坝多目标渗透系数反演过程中，采用传统线性参数反演分析方法已经无法用于解决多目标渗透参数反演优化[3-5]。随着计算机技术高速发展，越来越多的智能算法用于解决多目标非线性关系的预测，其中BP人工神经网络运用最为广泛。BP人工神经网络以其强大的自学习和自判断能力，能够有效地解决渗流参数之间非线性关系的优化。如郭海庆、吴中如等利用连续型Hopfield神经网络模型结合坝区现场实测资料对某堆石坝渗透系数进行有效反演[6]; 李守巨, 刘迎曦等根据渗流场的水头观测数据和注水试验先验信息，采用神经网络反演了吉林白山水电站坝基及防渗帷幕渗透系数，得到了较高精度[7]；骆进军, 李波等基于某拱坝原型观测资料采用BP神经网络对大坝坝基各岩层渗透张量情况进行了反演，并对结果进行了有效验证[8]。然而，BP人工神经网络在对样本集进行训练时，存在收敛速度不稳定、不能保证全局最优且拓扑结构不易确定的缺点，这些缺点将不利于BP人工神经网络进行多目标渗透参数的反演。针对上述缺点，本文拟采用GA遗传算法对BP人工神经网络参数进行优化，构建最优BP人工神经网络参数组合，达到加快计算速度并达到全局最优的目的。

本文以某黏土斜墙坝为研究对象，通过已构建GA-BP人工神经网络模型，对某黏土斜墙坝各介质分区渗透系数进行了反演计算，并将反演结果与传统BP人工神经网络计算结果进行了比较验证。

1 基于GA-BP的渗透系数反演分析方法

1.1 GA优化BP人工神经网络

BP人工神经网络训练精度及速度与网络结构层数、节点个数及初始权值和阈值有较大关系，当网络结构层数、节点个数确定的情况，初始权值和阈值的合理选择将对神经网络训练的好坏起决定性作用。针对最优初始权值和阈值参数组合确定难得的问题，本文通过GA遗传算法对其参数组合进行寻优，获取BP人工神经网络结构中的最优参数组合，赋予最优参数组合的BP人工神经网络具有较好动态自适应能力，能够有效克服BP人工神经网络收敛速度慢、不能保证全局收敛的缺陷[9]。根据GA遗传算法及BP人工神经网络的相关理论，本文通过MATLAB软件实现GA对BP人工神经网络权值和阈值的寻优过程，具体寻优步骤如图1所示。

图1 GA优化BP神经网络流程Fig.1 GA optimization BP neural network process

1.2 渗透系数反演模型

本文在对大坝各介质渗透系数的反演计算时，采用正交设计、有限元稳定渗流正分析及GA-BP人工神经网络相结合的反演方法。其中正交设计方法通过SPSS中的正交设计表从众多参数组合中安排数目较少的参数组合用于有限元稳定渗流正分析，从而大大减少渗流正分析计算的工作量；有限元稳定渗流正分析是将正交设计参数组合代入大坝有限元模型中进行渗流数值模拟，生成BP人工神经网络所需训练样本集；BP人工神经网络通过有限元稳定渗流正分析所得训练样本集构建各介质渗透系数组合与相应效应指标之间的非线性映射关系模型，从而通过输入效应指标实测值对渗透系数进行反演；由于BP人工神经网络在训练过程中误差反向的传播容易陷入局部最优值的特点，因此采用GA遗传算法对BP人工神经网络结构中的权值和阈值参数组合进行寻优，获取最优的反演参数[10-12]。BP神经网络网络模型如图2所示。

图2 BP神经网络网络模型Fig.2 BP neural network model

1.3 渗透系数反演流程

本文所建立的GA-BP人工神经网络多目标反演方法进行渗透系数反算的步骤如下：

(1)针对大坝实际结构分区情况，选取含有监测数据的剖面建立三维有限元模型用于进行渗流正分析。

(2)采用正交设计方法将待反演渗透系数在取值范围内选取若干个水平，设计获取相应的组合方案，并正交设计所得组合方案代入有限元模型进行稳定渗流正分析计算，获得GA-BP人工神经网络训练所需的样本数据集。

(3)以渗流正分析中测点压力水头为神经网络的输入层，坝体各介质的渗透系数为输出层，建立大坝各测点压力水头与各介质渗透系数组合之间的非线性映射关系。

(4)将大坝渗压计测点实测压力水头数据输入优化后的BP人工神经网络模型中，即可得到大坝所求各介质分区的渗透系数大小。

2 工程实例

2.1 工程概况

某黏土斜墙土石坝正常蓄水位55.00 m，校核洪水位57.14 m，总库容2 069 万m3，坝顶高程58.40 m，最大坝高19.8 m，坝宽6.0 m，坝顶长度667.0 m。为实时掌握了解工程安全运行情况，布置了较为齐全的渗压监测设施。本文以最大坝高典型断面处的压力水头观测资料实测值对该坝渗透系数进行反演，典型剖面渗压计布置在大坝建基面处，如图3所示。

图3 典型剖面渗压计布置Fig.3 Osmometer arrangement of typical profile

根据大坝的实际情况，建立典型断面三维有限元渗流模型，有限元模型计算范围：上、下游以坝踵、坝址为界各取2倍坝高，建基面以下取1.5倍坝高，如图4所示。模型采用六面体等参单元结合部分退化的四面体单元进行网格剖分，共划分单元19 548 个，节点数22 451 个。

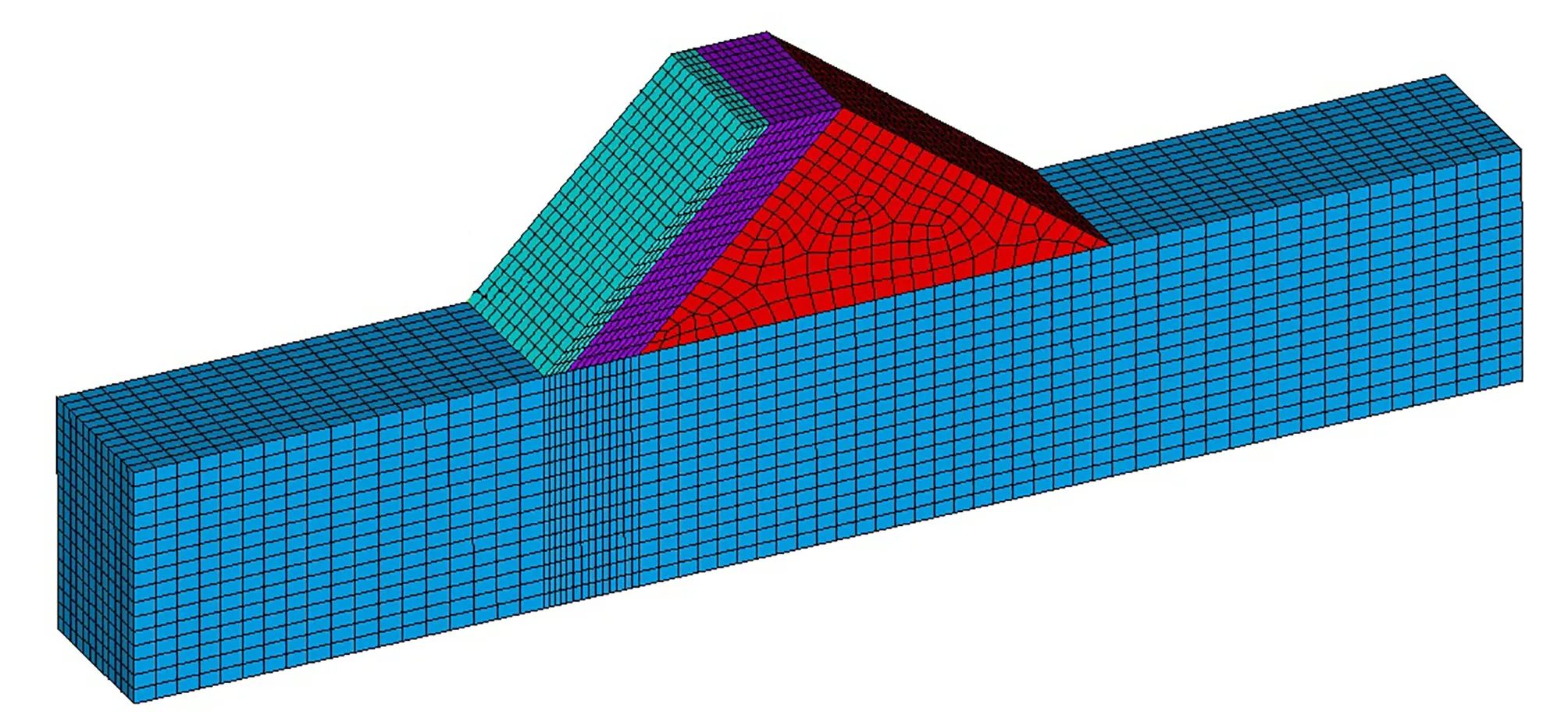
图4 典型坝段有限元模型Fig.4 Finite element model of typical dam section

2.2 计算过程

查阅该坝初设数据并结合工程经验，确定大坝黏土斜墙、上游坝体、下游坝体、坝基等介质渗透系数反演计算范围，如表1所示。

表1 渗透系数取值范围 m/sTab.1 Permeability coefficient range

BP神经网络模型结构的稳定性受训练样本集的数量多少影响较为敏感，渗透系数正交设计取黏土斜墙、上游坝体、下游坝体、坝基4因素按5个水平作为正交设计输入，输出17个待反演参数的组合，各水平取值情况如表2所示。将正交设计所得组合代入有限元模型中进行稳定渗流正分析，获取BP人工神经网络所需的训练样本样本集数据进行神经网络训练，其中P1～P4节点压力水头计算值为神经网络输入，大坝黏土斜墙、上游坝体、下游坝体、坝基等介质渗透系数取值为输出。本次渗透系数反演过程中，不考虑上游水位变化的影响，上游水位取常值，为正常蓄水位55.00 m。

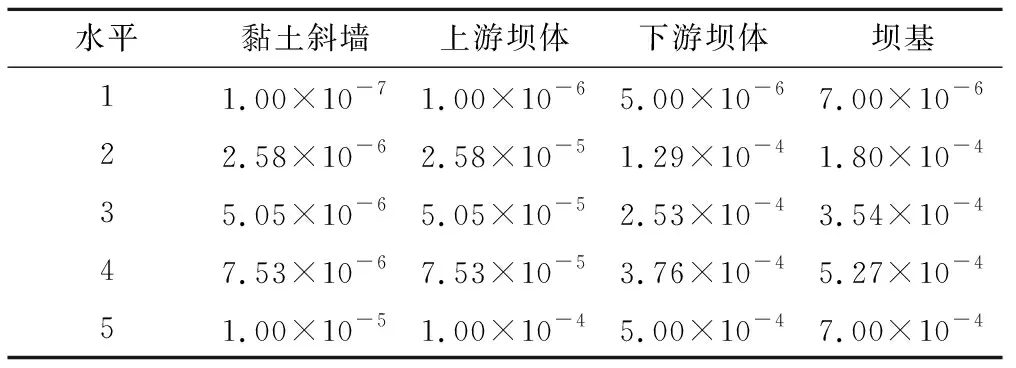
表2 基于正交设计渗透系数各水平取值 m/sTab.2 Value of each level of permeability coefficient based on orthogonal design

本文BP人工神经网络结构中隐含层层数取为1，隐含层神经元节点数取值通过常用经验公式进行试予以确定，经验公式如下：

(1)

式中：L为隐含层节点个数；m、n分别为输入层、输出层节点个数；a为常数，取1～10。

本文m=4、n=4，经过反复试算，当L=9时预测效果综合误差最小。GA遗传算法对BP人工神经网络结构中权值和阈值进行寻优时，种群个数取40，最大遗传代迭代次数取50，代沟取0.95，交叉概率取0.7，变异概率取0.01。

2.3 计算结果

利用渗压计P1～P4实际所测压力水头监测数据代入训练好的BP人工神经网络模型结构，模型输出数据即为大坝黏土斜墙、上游坝体、下游坝体、坝基等各介质分区的渗透系数反演结果，反演得到的各分区结果为K黏土斜墙=7.91×10-6m/s、K上游坝体=6.19×10-5m/s、K下游坝体=2.87×10-4m/s、K坝基=6.98×10-5m/s，通过观察上述反演结果可知基于GA-BP人工神经网络的多目标反演算法结果均处于相应的取值范围内。

为进一步检验该反演所得各渗透分区渗透系数大小的合理性，将反演所得各渗透分区渗透系数代入有限元模型中进行稳定渗流正分析，获取渗压计P1～P4测点的压力水头计算值，并与实测值进行对比，结果如表3所示。由表3对比结果可得，渗压计P1～P4测点压力水头计算值与实际测量值吻合较好，计算值与实测值之间相对误差在0.6%～3.6%之间，由此说明基于GA-BP人工神经网络的多目标反演算法得到的大坝各分区渗透系数合理、可行。

表3 渗压计P1～P4测点压力水头计算值与实测值Tab.3 The osmometer P1～P4 measured the point pressure and the measured value

2.4 GA-BP与BP人工神经网络计算结果对比

为比较GA-BP与BP人工神经网络计算效果的，本文单独采用不经GA遗传算法优化的传统BP人工神经网络建立渗透系数反演模型对渗压计P1～P4测点的压力水头进行计算，结果见表4。

表4 基于BP神经网络渗压计P1～P4测点压力水头Tab.4 Based on BP neural network osmometer P1～P4 measuring point pressure

对比GA-BP与BP人工神经网络计算结果可知：BP人工神经网络计算P1～P4测点压力水头误差范围2.0%～10.4%，该方法计算结果整体前者反演精度更低。同时利用MATLAB自带计时功能对上述两种模型训练时间进行对比，经过GA优化后的BP人工神经网络对样本进行训练时间为0.48 s，后者训练时间为1.14 s，显然经过GA优化后BP人工神经网络在训练样本数据集时收敛速度同样优于传统的BP神经网络。

3 结 论

(1)针对BP人工神经网络样本数据集训练收敛速度慢、目标值难以保证全局最优且结构不易确定等问题，引入GA遗传算法对其寻优后，在收敛速度及计算精度上都将有所提升。

(2)基于测点压力水头监测数据，采用GA-BP多目标反演算法所获得的各介质渗透系数，将其代入渗流正分析中得到的渗压计P1～P4测点压力水头计算值与实测值相对误差分别0.8%、3.6%、1.4%和0.6%，总体上与实测数据基本一致，表明GA-BP多目标反演算法合理可行，可望在水利工程其他参数反演领域进一步推广。