珠海市中珠联围降雨与潮位遭遇联合分布概率及内涝风险研究
张大伟,张 鹏,郭 珊,吴辉明
(1.广州珠科院工程勘察设计有限公司,广州 510610;2.珠江水利委员会珠江水利科学研究院,广州 510610)
珠海市位于珠江出海口西岸,濒临南海,大部分为冲击平原区,地势较低,受洪潮交汇作用、水文情势相当复杂,属于典型的平原感潮河网地区。珠海市受特有的地理因素影响,天文大潮、风暴潮与暴雨等灾害性天气频发,时常发生内涝,损失严重。当降雨量较大并遭遇外海高潮位时,涝水不能及时排出,引发洪涝灾害,造成重大经济损失,严重威胁着人民生命财产安全。中珠联围内涝与暴雨和潮水位密切相关,因此,研究中珠联围降雨与潮位遭遇联合分布,分析内涝发生的频率,为中珠联围内涝防治提供技术支撑。
目前,关于珠海市暴雨与潮位遭遇联合分布研究甚少,遭遇组合常采用统计分析和外包法处理[1]。由于暴雨与潮水位的空间相关性,区域暴雨与潮水位总有一定的联系,因此它们的联合分布函数不能将2者的边缘分布函数简单相乘而得到[2]。传统的雨潮遭遇统计分析方法无法考虑雨潮之间遭遇的内在联系,而Copula函数理论可以通过构造联合分布来描述降雨和潮位之间的内在联系,Copula理论的出现为构造多变量事件的相关关系和联合分布提供了一种新的理论计算方法[3]。该方法最早于1959年提出,20世纪末才被运用到金融领域,21世纪初才引入工程领域。近10 a多来,在多变量水文因素分析中,国内外[4-6]学者开始采用Copula函数来构建多变量的联合分布函数,研究多变量水文因素概率分布。林荣等[7]采用正态变换法分析了吴淞口设计潮位与不同频率区间降雨及相应黄浦江曲江降雨遭遇的概率,然而正态变换法在对原始数据进行转换处理之后,往往会导致一些数据失真,并不能保证处理后的数据呈正态分布[8]。刘曾美等[9]运用Copula函数研究了中山市坦洲镇涝区的暴雨和外江潮水位遭遇的联合分布。任锦亮等[10]采用AMH Copula函数研究了上海市台风降雨和潮位遭遇组合概率。
本文采用Copula函数建立区域暴雨和潮水位2变量之间的联合分布函数,用概率分布来描述2者遭遇的机率,并基于联合分布研究雨潮遭遇组合重现期的计算方法,通过实例探讨区域暴雨和潮水位遭遇的同现概率和内涝发生的概率及重现期。
1 Copula理论及降雨-潮水位联合分布模型
1.1 Copula理论简介
Sklar定理:设x、y为连续的随机变量,其边缘分布函数分别为Fx和Fy,F(x,y)为变量x和y的联合分布函数,如果Fx和Fy连续,则存在唯一的函数Cθ(u,v)使得:
F(x,y)=Cθ[Fx(x),Fy(y)],∀x,y
(1)
式中:Cθ(u,v)为Copula函数;θ为待定参数。
降雨h和相应的潮位z均为连续随机变量,F(h,z)为降雨和潮位联合分布函数,因此存在唯一的Copula函数使得F(h,z)=Cθ[Fh(h),Fz(z)]成立,Fh(h)、Fz(z)分别为降雨、潮位的连续边缘分布函数。
Copula函数是用来描述随机变量间相关性结构的函数,应首先对随机变量的相关性进行度量[11]。目前常用于度量水文变量间相关性的指标为皮尔逊线性相关系数和Kendall秩相关系数[3]。Kendall秩相关系数的计算公式为:
(2)
式中:sign(·)是符号函数,取值如下:
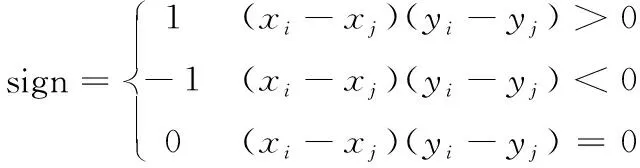
(3)
1.2 Copula函数选用
Copula函数中,采用阿基米德族Copula函数描述水文变量的研究越来越多,并已经初具理论和应用基础[4,12]。变量联合分布函数的性质和与之对应的Copula函数密切相关,因此,要根据变量h和z的相关性程度合理选择阿基米德族中的Copula函数。
降雨—潮水位联合分布函数实质上是将一个二元联合分布分为2个独立的部分来分别处理:变量间的相关性结构和变量的边缘分布,其中相关性结构用Copula函数来描述,边缘分布采用皮尔逊Ⅲ型曲线来描述。
内港站多年平均最高潮位为1.73 m,年最大24 h降雨遭遇最高潮位均值为0.91 m,相差较大,说明年最大24 h降雨基本与外江年最高潮位不遭遇;根据1960-2018年59 a降雨与潮位遭遇数据,仅有1 a相应潮位为年最高潮位,年最大24 h降雨量与相应最高潮位水位2变量的Kendall秩相关系数τ=0.004 1,说明这2变量相关性较弱,因此不适合用Gumbel Copula函数和Clayton Copula函数来描述它们之间的相关结构,可以选用AMH Copula函数或Frank Copula函数[3,13]来描述它们之间的相关结构。
如用AMH Copula函数描述降雨h和相应潮位z之间相关结构,则联合分布函数F(h,z)为:
(4)
τ与θ的关系如下:
(5)
如用Frank Copula函数描述降雨h和相应潮位z之间相关结构,则联合分布函数F(h,z)为:

(6)
τ与θ的关系如下:

(7)
2 降雨与潮位遭遇风险分析
降雨与潮位联合密度函数反映区间暴雨和潮位遭遇的机率,2者遭遇存在的风险一般用风险率和重现期来表示。风险率指一定条件下,非期望事件发生的频率,对于单变量来说,风险率为超值概率,因此对于降雨h和潮位z的风险率P分别表示如下:
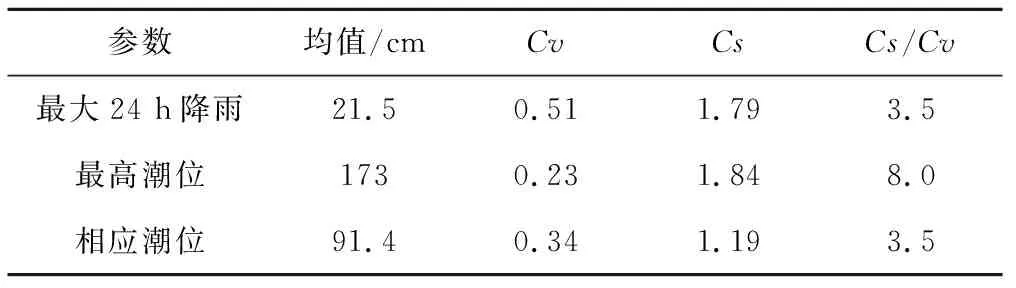
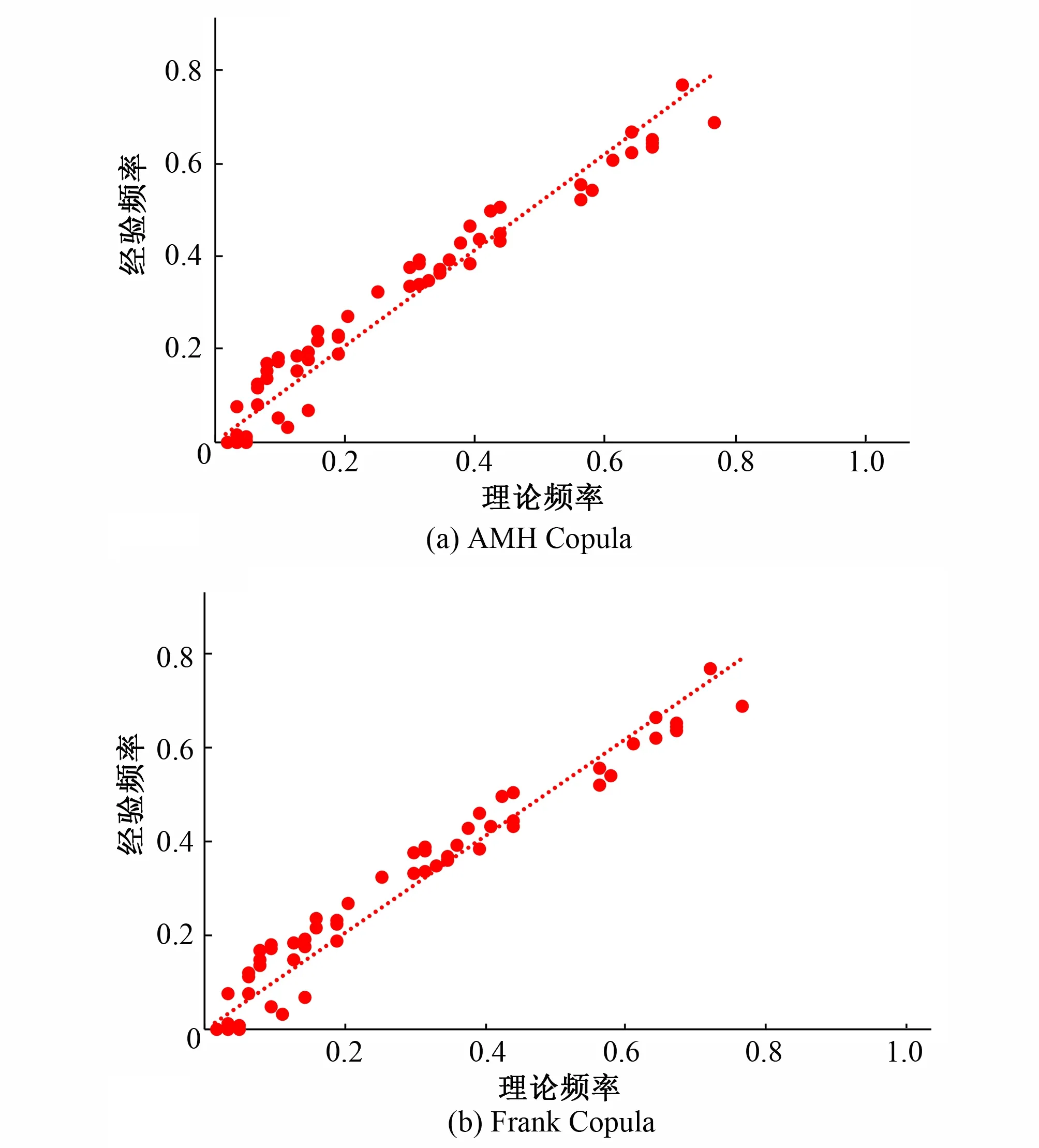
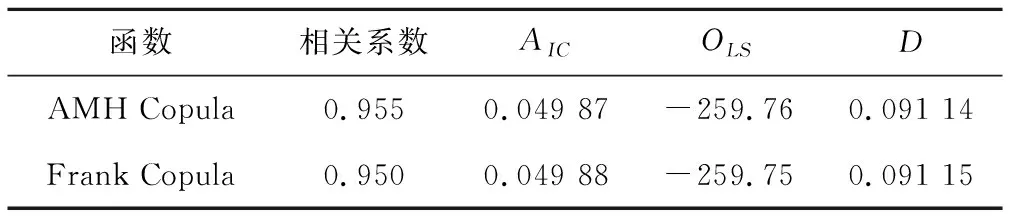
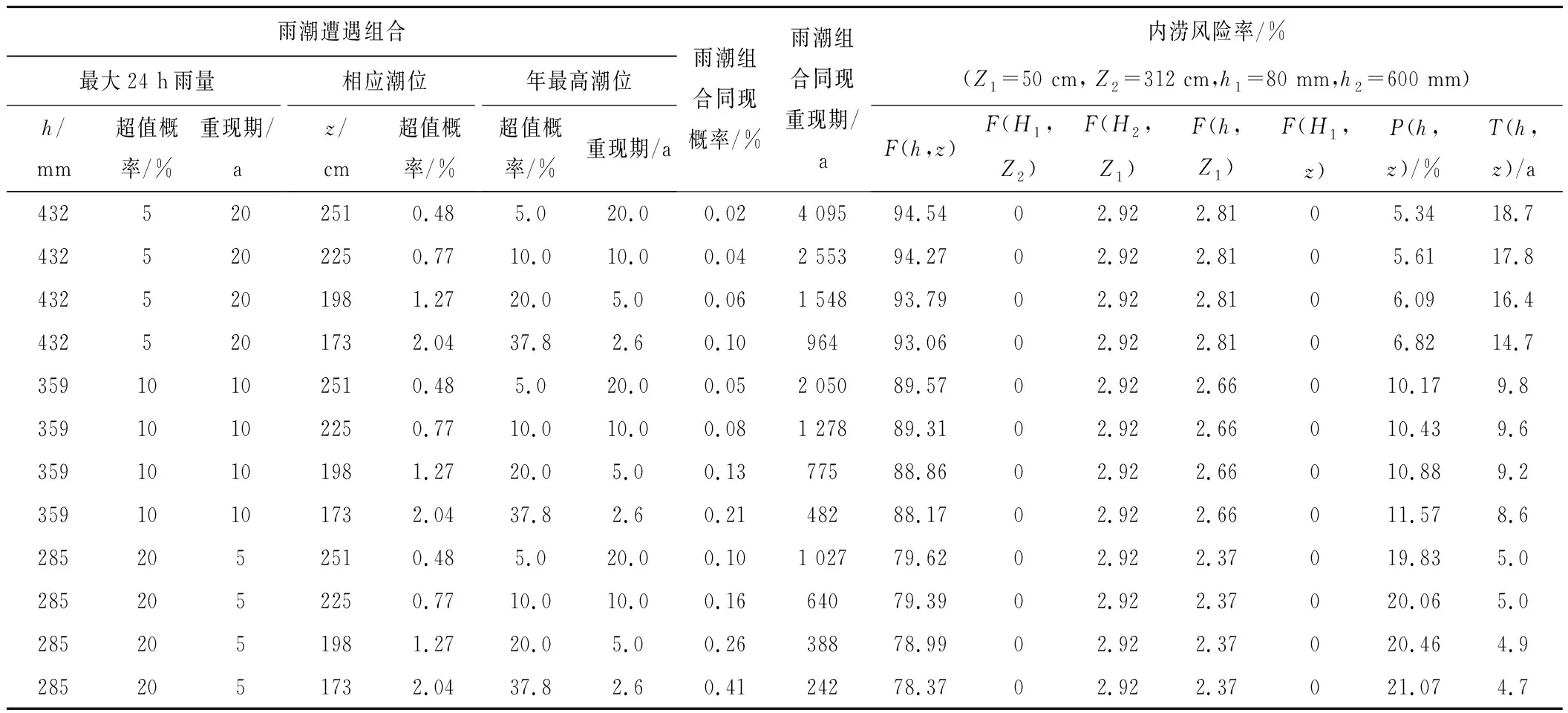
P(h)=P(h≥H)=1-F(h (8) P(z)=P(z≥Z)=1-F(z (9) 式中:H为设计暴雨;Z为排涝工况设计潮位。 超过某一特定值的重现期为风险率的倒数,因此对于降雨h和潮位z的重现期T分别表示如下: (10) (11) 对于中珠联围降雨和潮位遭遇关系有关的排涝问题,是指发生内涝风险可能造成对人们生命财产、社会公共交通等造成危害或构成不利影响。对于珠海市中珠联围发生内涝的风险来说,可采用降雨h与外海潮位z的函数表示。在中珠联围排涝设计暴雨和相应外海潮位条件下,以下3种情况不会发生内涝风险:①当降雨h≤H(设计暴雨)和潮水位z≤Z(排涝工况设计潮位)时,不会发生内涝;②当潮水位z>Z(排涝工况设计潮位)且不超过海堤设计潮位值Z2时,因中珠联围内河网密集高,调蓄空间大,只要降雨h≤H1(与河涌调蓄容积相关),即使中珠联围不向外排水的情况下,亦不会发生内涝;③当潮水位z≤Z1(多年平均低潮位)时,因中珠联围内河道排水和泄水闸排水能力强,只要降雨h≤H2(河涌过流及水闸泄流能力条件下相应降雨),亦不会发生内涝。因此发生内涝的风险区域见图1。 图1 内涝风险区示意图Fig.1 Drawing of waterlogging risk zone 于是,中珠联围内涝风险率采用下式表示: P(h,z)=1-F(H,Z)-F(H1,Z2)-F(H2,Z1)+ F(H,Z1)+F(H1,Z) (12) 如果采用水利标准重现期来表示内涝风险,则内涝重现期T(h,z)可采用下式表示: T(h,z)= (13) 往往涝区整治制定内涝标准时比较关心降雨和潮位均超过某一量级的概率,即P(h≥H,z≥Z),称为同现概率,其倒数为同现重现期,具体表达式如下: P(h≥H,z≥Z)=1-Fh(H)-Fz(Z)+F(H,Z) (14) (15) 珠海市中珠联围位于珠江口磨刀门水道东岸,邻近澳门。中珠联围主要通过前山河排渠湾仔水道,湾仔水道内设有内港潮位站,临近有神湾雨量站,因此,采用神湾雨量站1960-2018年的历年最大24 h量以及内港潮位站的相应潮位来分析确定最大24 h雨和其相应潮位的联合分布,计算步骤如下: (1)确定单变量降雨、相应潮位及年最高潮位的P-Ⅲ型曲线。 (2)利用式(2)、式(3)计算Kendall秩相关系数τ。 (3)利用式(16)、式(17)统计样本经验频率,判断其拟合效果。 (4)择优选取联合分布函数,计算降雨与潮位同现概率及内涝风险率。 神湾站年最大24 h降雨、内港站相应最高潮位和年最高潮位均服从P-Ⅲ型曲线分布,本文采用矩法对降雨、相应潮位和年最高潮位的参数进行估算,并结合适线法优化估算参数,得到年最大24 h降雨、相应潮位和年最高潮位的统计参数,见表1。 表1 P-Ⅲ型曲线参数估算成果Tab.1 Estimated results of P-Ⅲ curve parameters 根据神湾站和内港站实测资料,利用式(2)和式(3)可计算得到最大24 h降雨和相应潮位的Kendall秩相关系数τ=0.004 1。说明神湾站年最大24小时降雨与内港相应潮位相关关系很弱。利用相关性指标法[9],采用式(5)、式(7)分别计算得θ为0.018 4和0.036 9。 为选定最大24 h降雨与相应潮位拟合最高的Copula函数,需对Copula函数进行检验,本文采用K-S检验来评价2变量的理论联合概率分布函数与经验联合概率分布的拟合程度。 假设第i对联合观测值(hi,zi),按降序排列后对应为(j,k),则(hi,zi)的累积经验频率Femp(hi,zi)可由下式求得: Femp(hi,zi)=P(h≤hi,z≤zi)=P[h≤h(j),z≤z(k)]= (16) 式中:n为样本数量;j为hj的排序号;k为zj的排序号;nm,l为符号函数,取值如下: (17) K-S检验统计量D计算公式如下: (18) 除K-S检验外,还需根据评价指标选取最适合的Copula函数。本文选取理论联合分布概率与经验联合分布概率适线、离差平方和最小准则(ΟLS)以及AIC信息准则来评价,并选取ΟLS和AIC最小的Copula作为联合概率分布函数[9]。其计算公式如下: (19) AIC=nln (MSE)+2K (20) 式中:K为模型参数的个数,取59。 (21) 神湾站最大24 h降雨与内港相应潮位其经验联合分布值与理论联合分布值散点均落在45°对角线附近,见图2。其误差来源于经验联合分布由实测数据统计,统计过程中小于一定数值的计为1,否则计为0,而没有中间数值,导致经验频率与理论频率具有一定的误差。另外Copula函数仅能近似表达雨潮相关关系用,其误差主要来源于以上2个方面。虽然经验分布与理论分布存在误差,但AMH Copula函数拟合相关系数达0.955,Frank Copula函数拟合相关系数达0.950,拟合效果良好,雨潮联合分布可采用Copula函数来表示。离差平方和最小准则(ΟLS)、AIC信息准则指标和K-S检验统计结果见表2。 图2 降雨与潮位联合理论分布与经验分布散点图Fig.2 Scatter plots of theoretical and empirical distributions of rainfall and tide levels 表2 拟合检验统计量Tab.2 Fitting test statistical scale 由表2可知,2种Copula函数均能通过K-S检验,且与联合经验频率拟合很好,说明所采用的Copula理论联合分布函数是合理的,根据拟合度检验统计量结果,本文选用拟合效果更优的AMH Copula函数来描述神湾站最大24 h降雨与内港相应潮位的联合概率分布,其联合分布函数如下: (22) 根据神湾雨量站和内港潮位站的最大24 h暴雨、相应潮位的边缘分布,计算不同重现期下的降雨和潮位组合,对于给定的相应潮位,在年最高潮位频率曲线中对应一定的频率,从而计算得到相应潮位的年重现期。 由式(22)可求得降雨和潮位的联合分布概率,由式(12)、式(13)可求得中珠联围内涝的风险率及重现期,由式(14)、(15)求得设计雨潮遭遇组合同现概率及重现期。表3给出了不同频率降雨、潮位组合的概率及中珠联围内涝的风险率和重现期。 由表3可知,中珠联围发生20 a一遇暴雨与2 a年一遇、10 a一遇、5 a一遇、多年平均最高潮位遭遇同现概率分别为0.02%、0.04%、0.06%和0.10%;10 a一遇暴雨与20 a一遇、10 a一遇、5 a一遇、多年平均最高潮位遭遇同现概率分别为0.05%、0.08%、0.13%和0.21%,遭遇概率较低,说明中珠联围发生10 a一遇以上降雨时,遭遇多年平均最高潮位以上潮位的几率非常小;根据《珠海市流域综合规划修编》,中珠联围内涝防治标准采用20 a一遇最大24 h设计暴雨不成灾,外江遭遇5 a一遇最高潮位,由雨潮遭遇同现频率及重现期分析可知,20 a一遇暴雨遭遇5 a一遇高潮位组合的同现频率为0.06%,重现期为1 548 a,远高于内涝防治标准的20 a一遇。 然而,中珠联围实际内涝的情况并非暴雨、潮位同时超过设计值时才发生内涝,因此中珠联围发生内涝的概率要远大于雨潮组合同现概率。根据表3计算结果,当中珠联围发生20年一遇暴雨遭遇外海20 a一遇、10 a一遇、5 a一遇、多年平均最高潮位时,发生内涝的概率分别为5.34%、5.61%、6.09%和6.82%;当中珠联围发生10 a一遇暴雨遭遇外海20 a一遇、10 a一遇、5 a一遇、多年平均最高潮位时,发生内涝的概率分别为10.17%、10.43%、10.88%和11.57%。发生内涝的概率均高于暴雨频率,重现期低于暴雨设计重现期。 表3 遭遇组合概率和内涝风险计算成果Tab.3 Calculation results of encounter combination probability and waterlogging risk (1)采用P-Ⅲ型分布曲线拟合珠海市中珠联围最大24 h降雨、相应潮位和年最高潮位,采用矩法估算曲线参数,结合适线法优化估算参数,得到不同重现期的设计值,并运用Copula函数构建最大24 h降雨和相应潮位的联合分布模型,通过理论分布值与K-S检验,表明AMH Copula函数能较好地拟合其联合分布。 (2)考虑中珠联围内河涌及排水闸泵条件,构建内涝风险率计算模型及雨潮同现频率计算模型,最后给出不同雨潮组合的内涝风险率及同现频率。 (3)根据计算结果,中珠联围内涝风险率大于设计暴雨重现期,远大于雨潮同现概率;分析中珠联围内涝风险率为治涝工程的暴雨和潮水位的遭遇组合确定提供参考,明确发生内涝的风险率。中珠联围20 a一遇最大24 h设计暴雨遭遇外海5 a一遇高潮位设计工况条件下,内涝发生的概率为6.09%,重现期为16.04 a。 (4)根据内涝发生概率可知,中珠联围内涝发生的重现期低于暴雨设计重现期,中珠联围内涝整治工程实施过程中,应适当增加工程规模,使内涝发生重现期与设计暴雨重现期相适应。 (5)本文构建的降雨和相应潮位的二维联合分布,主要考虑暴雨和外江潮水位顶托可能形成内涝的组合风险,若考虑防潮风险可分析潮位与相应降雨的联合分布函数来考虑,但对于一个完整的防洪封闭圈而言,不能简单采用Copula函数分析防洪、防潮、防涝综合风险概率及重现期,需进一步研究。
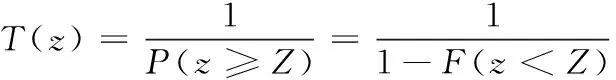

3 实例分析
3.1 单变量和联合分布参数的确定
3.2 拟合效果评价
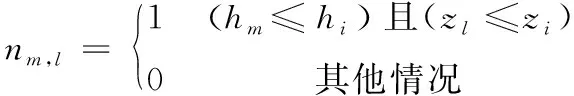
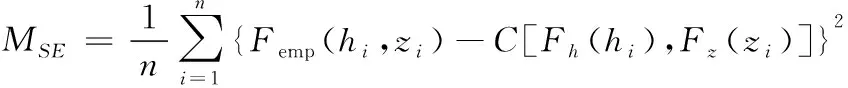
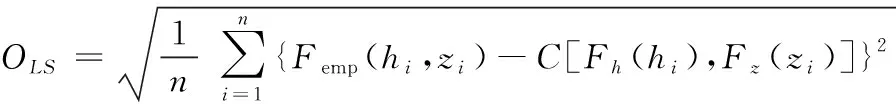
3.3 组合遭遇频率和内涝风险分析
4 结 论

