布置压电阵列元件薄壁结构的振动控制技术研究

李凯翔

（中国飞机强度研究所，西安 710065）

现代高性能军用飞机的设计正在向轻质、高速、高机动和隐身方向发展，这一发展思路也带来了严重的振动和噪声问题。由于飞机结构重量系数降低，飞机典型结构（如飞机壁板）很可能发生较为剧烈的振动。这些振动不但会使飞机驾驶员和乘客产生不适，导致的振动疲劳/声疲劳问题也直接威胁着飞机的飞行安全。目前，经常采用的抑制飞机壁板振动的工程方法是提高刚度（如增加筋条）和布置阻尼（粘贴阻尼材料），但这些被动的控制方法对低频振动控制效果不佳，而且过多地增加结构重量也与轻量化设计理念相悖。军机结构的低频振动控制一直是亟待解决的技术难题。

近年来，采用周期压电分流阻尼技术的结构振动控制方法成为了研究热点[1-5]。将连接分流电路的压电片周期性地粘贴到基体结构上，形成压电分流阵列，可以实现机械能、电能和热能之间的转换，已达到调控基体结构中弹性波传播的目的[6-10]。类比固体物理学中的晶体，可以将布置压电分流阵列的复合结构看作由单个晶胞在空间上周期性排布形成的一种晶格结构。其晶胞主要包括三个部分，即基体结构、压电片和分流电路。基体结构一般选择被控对象的基础构件，如被控结构中的梁或板等，基础构件为振动传播载体，收到振源的激励，弹性波会在被控结构中传播，从而造成结构的振动或噪声辐射。压电片属于换能单元，通过压电效应实现振动机械能和电能之间的转换。分流电路属于控制单元，对转换的电能进行控制，如阻尼耗散（电阻）或者动力吸振（谐振）等。因此，在分流电路及压电元件的共同作用下，能够实现对基体结构中弹性波传播特性的调控。

压电分流技术最早由Forward 于1979 年提出，Hagood N W 和Von Flotow A 从压电材料的机电耦合特性出发，分析了耦合于结构中的连接有电阻或电感的压电元件对结构动力学特性的影响，对压电分流系统的工作原理和电路参数的优化问题进行了全面的理论分析和实验验证，他们的研究工作为压电分流技术的发展奠定了基础，具有里程碑式的意义[11]。1998年，美国宾夕法尼亚州立大学的George A. Lesieutre根据压电分流电路的构成，将其分为四种基本型分流电路：电阻型分流电路（resistive shunt）、电感型分流电路（inductive shunt）、电容型分流电路（capacitive shunt）和开关/转换型分流电路（switched shunt），如图1 所示[12]。

各种分流电路的区别在于构成分流电路的元器件不同，各种分流电路具有不同的电学行为[13-16]。电阻型分流电路通过电阻散热消耗能量，起到减振效果；电感型分流电路中的电感和压电元件本身固有的电容组成LC 谐振电路，起到类似于被动式的机械吸振器（Passive Mechanical Vibration Absorber，PVA）的作用；电容型分流电路通过并联于压电元件本身固有的电容两端的多个电容来改变压电元件的有效刚度，来满足对结构参数（如刚度）的特定要求；开关/转换型分流电路控制结构刚度在高和低两个状态之间的相互转换或将结构的振动能量转化为其他有用的形式[17-18]。

近年来，随着声子晶体和声学超材料概念的提出，布置压电元件阵列的结构也作为一种声学超材料，得到越来越多的关注。Kader 等人最早针对周期压电元件梁，采用主动方法开展了结构振动抑制研究，但主动方法需要耗费较多的外界能量[19]。随后，Kader 等人采用R-L 被动电路对结构进行了控制，实现了对结构第一阶振动模态的控制[20]。Vidoli 等人发展了一种多分支分流电路，可以实现对结构多个模态振动的同时抑制[21]。Bao 等人采用开关型压电分流阻尼电路，对周期压电梁结构开展了振动控制研究，对比了电阻型、电感型和开关型的抑振效果，指出周期开关型压电分流技术拓宽了布拉格带隙，为低频振动控制提供了一种新途径，如图2 所示[22]。Zhang 等人在各向同性板的上下表面对称布置了周期压电元件阵列，在压电元件两极分别连接了电感型和负电容型分流电路，并发展了一种有效的媒介法，用于预测这种智能壁板的隔声系数，如图3 所示[23]。

1 压电元件数学模型

压电效应有两种：一是正压电效应，描述材料将机械应变转换为电荷的能力；二是逆压电效应，将施加的电势转化成机械应变能的能力。正压电效应使材料具有成为传感器的能力，而逆压电效应使材料具有成为作动器的能力。材料具有将电能转化为机械能或将机械能转化为电荷能的能力时，就认为其具有压电性能。

图2 布置周期压电阵列的梁结构（开关型分流电路）Fig.2 Beam structure with bonding periodic piezo-patches (switch type shunt circuit)

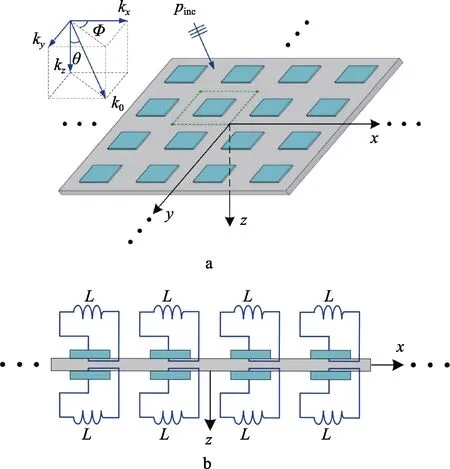
图3 布置周期压电阵列的板结构（电感型分流电路）Fig.3 Plate structure with bonding piezo-patches array(inductance type shunt circuit)

压电材料属于铁电材料，未极化的压电材料本身存在正负电荷重心不重叠，自发产生偶极子，但其自发极化是紊乱取向的，此时没有压电性。对这种陶瓷施加强直流电场进行极化处理，原来混乱取向的自发极化就沿电场方向择优取向。去除电场后，陶瓷仍保留着一定的总体剩余极化，于是使陶瓷有了压电性能。压电材料的力学和电学性能可以用两个线性化本构方程来建立模型，这些方程包含两个力学变量和两个电学变量。正压电效应和逆压电效应可以用式（1）和式（2）两个矩阵方程来建立模型（IEEE 压电标准，ANSI 标准176—1987）[24]。

式中：[D]为电位移矢量；[T]为应力矢量；[e]是介电常数矩阵；[cE]是常电场强度下的弹性系数矩阵；[S]是应变矢量；[ ]αS是常应变下的介电矩阵；[E]是电场矢量。

2 布置压电元件阵列飞机壁板结构的建模

2.1 压电材料在ANSYS 软件中的建模方法

ANSYS 中共用6 种单元可进行压电结构的建模，分别是SOLID5、PLANE13、SOLID98、PLANE223、SOLID226 和SOLID227，其中，较低编号的单元（如SOLID5）采用的形函数阶数较低，已经不太常用。以附加压电元件的薄壁结构为研究对象，薄壁结构采用 SHELL181 单元进行建模， 压电元件采用SOLID226 进行建模。

2.2 压电结构单胞元的建模与仿真

在压电结构单胞元的建模中，薄板的长宽高分别为1.2 m×1.5 m×0.005 m，压电元件的长宽高分别为0.12 m×0.15 m×0.001 m。薄板材料为铝板，弹性模量为70 GPa，密度为2 780 kg/m3，泊松比为0.33。压电元件采用PZT5 材料，其密度为7 850 kg/m3，压电元件的其他参数可在ANSYS 内通过填写APDL卡片进行定义，具体参数的定义方法和定义值如图4所示。

通过APDL 建模定义薄板和压电元件的几何尺寸，并进行了参数化几何建模。采用上述材料参数对结构进行了有限元网格划分，并分别对压电元件上表面和下表面节点强制等电位移，对薄板一段节点进行了全自由度位移约束，使薄板成为一个悬臂结构，如图5 所示。

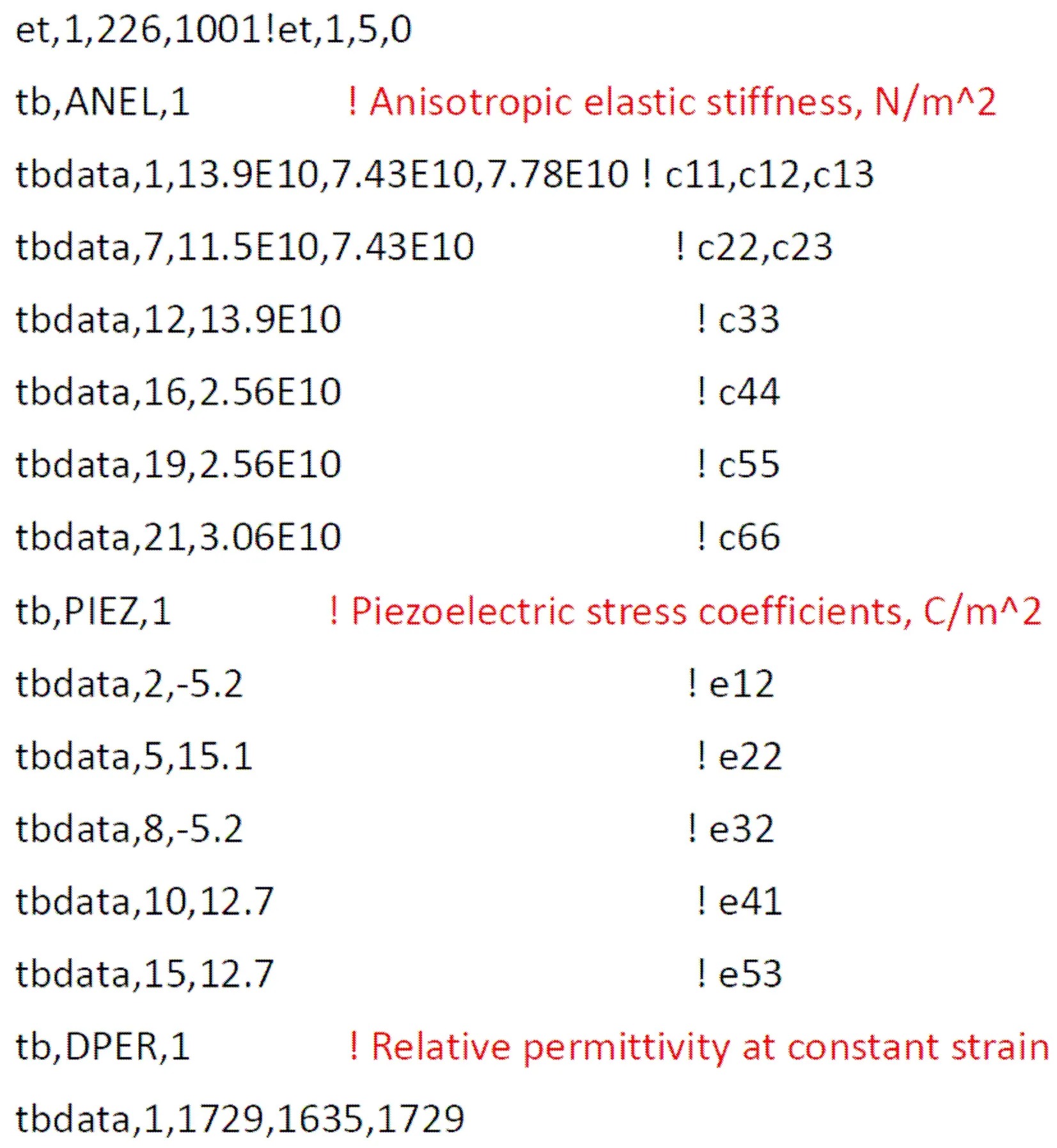
图4 ANSYS 中对压电元件材料参数的定义方法Fig.4 Parameter definition of piezoelectric material in ANSYS APDL

图5 压电单胞元结构Fig.5 A cell of structural element with a piezo-patch

对压电单胞元自由端施加周期力，进行谐响应分析（Harmonic），并输出压电单胞元端部中点的位移和压电元件上表面的电压。图6 给出了压电元件上表面电压与图5 右下角上表面节点位移的曲线。由于压电元件各区域应力分布与振动振型相关，所以两者出现峰值的时刻不一定相同。对图5 所示结构（单边固支）来说，第二阶模态（扭转振型）的节线为压电片的水平中轴线，因此在结构处于第二阶共振模态时刻，由压电效应诱发的上表面各单元电荷极性表现为：当节线上方单元产生正电荷时，节线下方的单元则会产生负电荷，反之亦然。因此，由于正负极性相消的作用，这阶模态产生的电荷量约为0。

图6 压电单胞元电压与端部位移的响应曲线Fig.6 Response curve of piezoelectric cell voltage and tip displacement

2.3 布置周期性压电结构的建模

对2.2 节中的压电单胞元沿x方向和y方向进行复制（x方向5 份，y方向3 份，共15 份），并耦合交接处的节点，形成周期性压电复合板结构，如图7所示。将压电元件上下表面节点全部进行等电势设置，由于压电元件在电学上可等效为一个电容器，因此这种等效方式等同于将所有压电片进行并联。采用CIRCU94 单元分别定义了电阻R和电感L元件，并设置了一个独立节点将电感和电阻串联起来，最后和等效电容的两极进行连接，形成一个LCR 谐振电路，如图8 所示。由图8 可以看出，由于电路中的电容是并联的方式，因此所有压电元件可等效为一个电容器C=15C0。最后，对薄板结构的四个边进行固支约束。

图7 布置压电元件阵列的薄壁结构Fig.7 Thin-wall structure with piezo-patch array

图8 LCR 等效电路Fig.8 LCR equivalent circuit

3 布置压电元件阵列飞机壁板结构的仿真

3.1 布置周期压电元件薄板的谐响应分析

一般来说，压电分流阻尼技术只在结构的固有频率处起到减振作用。因此，本研究首先进行结构的谐响应分析，掌握0～200 Hz 频率范围内的结构谐振频率和压电元件电压情况。在薄板结构结合中心点施加周期力，提取结构不同位置的位移响应和压电元件上表面的电压响应，计算结果如图9 所示。图9 给出了布置压电元件阵列的薄壁结构位移与压电元件电压响应曲线，从仿真结果可以看出，压电元件的电压输出峰值与结构位移峰值并不是一一对应的关系，这是由于结构多阶模态都属于对称模态，这样不同压电元件产生的电压有着相位相反的关系，从而造成输出电压较低的结果。若使每片压电元件都能实现最大的机电转换效率，则需要分别组成控制回路。

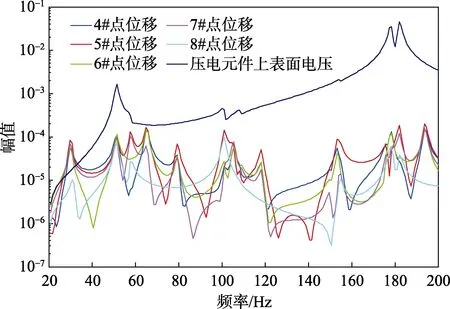
图9 布置压电元件阵列的薄壁结构位移与压电元件电压响应曲线Fig.9 Response curve of displacement of thin-wall structure with piezo-patch array and voltage of piezoelectric element

3.2 外接R-L 电路时的减振效果仿真

选取薄板结构第一阶固有频率（35 Hz）作为减振目标，在结构几何中心处施加周期力使得结构处在共振状态，同时，接通电路组成一个LCR 电路进行时域仿真。每个压电元件的电容C0可由公式（3）进行计算：

式中：ε3是压电元件3 方向的介电常数；S为压电元件的面积；k为静电常数8.9875×109；d为压电元件的高度。将所有压电元件进行并联后，等效电容C=15C0。

根据LCR 振荡电路特性，可得到LCR 振荡电路公式如下：

将第一阶固有频率f、等效电容C和电阻（这里设定为10 Ω）带入上述公式，可得到电感L为11.3 H。仿真时间设定为3 s，图10 给出了时域仿真的结果，可以看出结构振动得到了有效控制，也验证了本仿真方法的有效性。

4 总结

针对布置周期压电元件壁板结构的振动抑制进行了研究，采用ANSYS APDL 语言建立了耦合压电元件壁板结构的机电耦合模型，机电耦合模型可反映出结构振动响应与压电元件电压之间的关系。同时，通过电学有限元单元实现了压电元件的外接R-L 电路，最终建立了含有压电分流阻尼电路的典型壁板结构有限元分析模型，并开展了减振效果时域仿真，仿真结果验证了本方法的有效性。