复材结构刚度与隔声量的计算及参数优化∗
林 森 胡 莹 李晨曦 丛 昊
(中国商飞上海飞机设计研究院 上海 201210)
0 引言
当前航空航天科技的发展和其追求性能、结构效率、经济性优先的需求,继高性能合金材料之后,复合材料(以下简称“复材”)成为另一种高性能材料被广泛应用[1]。在民机领域,复材应用发展非常迅速,如B787 机身段采用全复材结构,复材用量达到50%,而空客A350XWB 飞机的复材用量约为52%[2−3]。复材尤其是层压板复材的应用,其优势是可以减重和提高疲劳耐久性,相比金属材料在结构上可减重20% 以上,而且由于层压板分层铺贴固化后,裂纹仅可能在层间扩展,疲劳性能大大得到提高,这是其他先进技术难以达到的效果[1]。复材的结构布局和铺层方式是影响复材结构刚度、强度和质量的两个主要因素,针对复材结构的布局和铺层方式优化,国内外研究人员开展了大量的研究工作,主要是通过算法进行铺层优化设计,获取目标函数以及影响参数从而获得最佳铺层[4−7]。但这类研究多数基于理论分析和实验室数据,且假定一些前提条件,与工程实际应用还存在一定差异。同时该类研究更多的关注刚度和强度,并未考虑对声学性能的影响。
结构的稳定性承载能力主要取决于结构刚度。工程中经常采用0◦、45◦和90◦铺层角度,控制45◦铺层的比例可提高层压板的屈曲承载能力。一般来说,复材结构设计采用均衡对称方式以消除复材层间耦合效应。本文基于复材经典层压板理论,在限制重量的条件下,调整铺层比例和方式来获取最佳刚度和强度,从而满足工程应用。另一方面,由于复材的可设计性较强,带来了强度和重量优势,但同时也造成了隔声性能的损失。与传统金属壁板结构相比,复材壁板在中高频上的隔声性能明显下降,必须在设计前期进行降噪设计。机身结构复材化之后,将是承担隔离大部分外部噪声的主要部件,且复材板壳的声学特性研究对结构的低噪声设计具有重要的意义[8]。研究发现,复材结构的铺层、角度、铺设方式等都对结构的隔声性能有着极大的影响[9−10]。鉴于复材的可设计性,在设计之初通过对铺层的参数进行分析,在满足结构刚度指标的前提下,开展隔声参数优化设计,最大程度地提高复材结构的隔声性能,节约重量成本。
基于上述原因,本文以某复材壁板为对象,首先在铺层数和铺层比例不变的条件下,分析不同铺层构型对结构刚度的影响。然后利用统计能量分析法(Statistic energy analysis,SEA),进一步对不同构型的复材结构进行隔声性能分析,确定铺层角度对结构隔声性能的影响,并与测试结果进行对比分析,验证分析模型的有效性和符合性。最后针对复材壁板进行声学处理,以铺设在复材壁板上的隔音棉厚度和密度为两个优化参数,分析不同厚度和密度的隔音棉的插入损失,并进行参数最优化分析,寻找最佳组合方式。
1 理论基础
1.1 复材结构经典层压板理论
1.1.1 单向铺层等效参数计算
复材指纤维与基体材料的混合物,形成的配置使两种组分中某些最佳特性加以结合。复材的构建单元为铺层或单层片,可对不同方向和材料的铺层进行组合,形成层压板,在飞机机身结构中常使用的复材结构组合为碳纤维和环氧树脂或酚醛树脂等[11]。铺层或单层片可以看成一个各向同性材料即树脂与碳纤维的组合,见图1。

图1 单层碳纤维环氧树脂复材结构组合示意图Fig.1 The two-part composite of a typical carbon fiber-epoxy composite
单层复材沿纤维方向的弹性模量Ex可以表示为

其中,Ef表示碳纤维的弹性模量;Em表示树脂材料的弹性模量;Vf=Af/A与Vm=Am/A分别表示碳纤维和树脂材料的容积率。
根据应力σ与应变ε的关系,复材结构沿垂直纤维方向的应变εy可以表示为

则单层复材沿垂直纤维方向的弹性模量Ey可以表示为
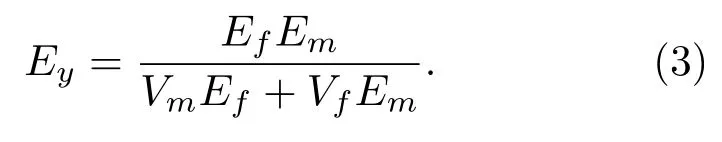
同样根据剪切变形一致可以推出平面内的剪切模量Gxy的计算公式:

其中,Gf表示碳纤维的剪切模量;Gm表示树脂材料的剪切模量。
1.1.2 复材结构层压板理论
将单向铺层按不同方向顺序进行铺叠,形成多层复材结构,即层压板。不同铺层角度的层压板,其各个方向的力学性能与角度有关系,其整体结构可以等效成平板结构,等效的平板结构在弯曲性能上与实际结构相同。研究表明[11],复材的等效耦合弯曲以及拉伸刚度可以通过每一层各向异性材料的弹性属性以及材料厚度及位置来进行计算。如图2所示,每一层铺层xOy坐标系与整体结构1O2 坐标系的刚度转换可表示为

其中,表示与整体结构1O2 坐标系呈θ角度的铺层刚度矩阵系数;Qxx、Qyy、Qxy、Gxy分别为单向铺层在xOy坐标系下的刚度矩阵系数和剪切模量;m=cosθ,n=sinθ。
对于薄壁复材结构(即层压板的厚度比结构的其他尺寸小得多),层压板承载可视为处于平面应力状态,根据应力应变关系,可得到复材结构层压板(包括薄膜-弯曲耦合)的广义本构关系:

因此,层压板的弹性刚度系数可由单层的材料刚度参数和相对位置表示为

其中,zk为沿z方向的第k层单向铺层中心面与底面的距离,见图3;(ij)k是第k层单向铺层的刚度;Aij、Dij、Bij分别为层压板的拉伸刚度、弯曲刚度、拉伸-弯曲耦合刚度矩阵系数。

图2 单层铺层坐标系转换示意图Fig.2 Positive rotation of principal material axes from x-y axes

图3 板结构纤维铺层示意图Fig.3 The laminates layup of the panel
1.2 复材平板结构声振分析
利用无限大薄板理论[12],具有对称性的复材平板结构弯曲波振动方程可表示为[9,13]
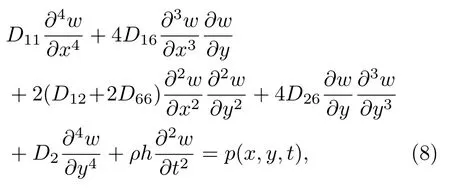
式(8)中,ρ为板的密度,h为板的厚度。对于各项同性板来说,D11=D22=Eh3/12(1−v2),D12=vD11,v为泊松比,D66=Gh3/12,且D16=D26= 0。对于正交结构,D11D22,D16=D26= 0。但大多数复材结构都是各项异性的,因此D16、D26不为0。
在进行复材壁板结构的隔声性能分析时,吻合效应是必须考虑的现象。当入射声波频率大于板的临界吻合频率时,发生吻合效应现象。当复材平板阻尼为0 时,其最小临界吻合频率可用式(9)计算[9]:

式(4)中,θi为入射声波与板的法向z轴的夹角;ϕi为入射声波投射到板的平面上,与x轴的夹角。
1.3 复材曲板结构隔声分析
SEA 方法是解决大型结构中高频噪声问题的常用方法之一,基于能量平均的原理,对结构细节可模糊处理,计算速度快,其精确度取决于子系统的划分、敏感参数的获取以及外部声源的输入[14]。工程中常用VA One 软件对结构进行建模,对于复材结构,VA One 软件也是基于复材平板结构声振分析模型计算结构的传声损失,且基于公式(9)的原理计算复材结构的吻合效应频率。
在声载荷下通过板的振动传递的声能量可以理解成是由3 部分影响的[15−16]:(1)声源的压力谱Gpp(ω);(2) 结构的模态阻抗Zmn=µmn与声阻抗Z0=ρ0c0的比率;(3) 模态辐射效率σmn(ω)。因此板在带宽∆ω内的辐射能量可表示为
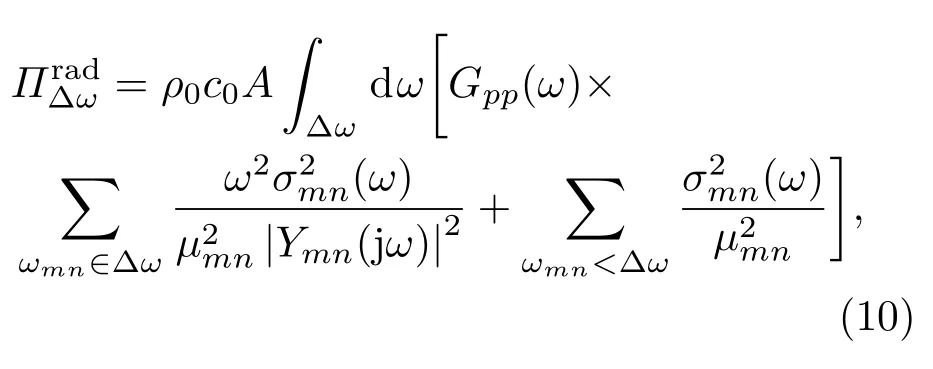
其中,表达式右边第一部分是在带宽∆ω内的共振模态响应辐射的声功率,第二部分是非共振质量控制辐射(质量定律)的功率。可以知道,一个具有高刚度质量比率的复合板,在共振频率下不会有很高的模态阻抗Zmn,除非模态阻尼非常高,这时模态阻抗可以写成Zmn(ωmn) = jηmnµmnωmn。如果模态阻尼很高,那么板上的振动响应会相应的减弱。然而,振动响应的降低并不是一定意味着具有更高的隔声量,这是因为振动的减弱通常伴随着辐射效率的增加,而整体的隔声量受到振动速度和辐射效率的综合影响。SEA方法中定义结构的有效隔声量为

其中,A为结构有效传递面积;c1为声波在声源室的传播速度;E1、E2分别为声源室和接收室空腔子系统能量;n1、n2分别为声源室和接收室空腔子系统的模态密度。
2 复材结构刚度分析
本节首先考虑结构布局和铺层形式对复材结构刚度的影响,以某机型复材壁板为分析对象,尺寸约为2100 mm×1600 mm,具体参数见文献[10]。在总铺层数和铺层比例不变的前提下,给出可能的其他几种构型,见表1,分析不同铺层构型对结构刚度的影响。

表1 不同铺层构型的复材结构Table 1 The composite skins with different configuration
图4 给出了单向铺层(0◦,±45◦)和不同铺层构型的复材整体结构弯曲刚度在极坐标下的分布。可以看出,(0◦,±45◦)的单向铺层弯曲刚度分布量级一致;不同铺设角度顺序对复材整体结构的弯曲刚度有影响。图5 给出了不同铺层构型的复材整体结构弯曲刚度矩阵系数D11、D12、D22、D16、D26、D66在极坐标下的分布。可以看出,不同铺层构型的复材整体结构弯曲刚度均呈现出对称且弱耦合性能,其中,构型1 和构型4 的弯曲刚度参数与原构型类似;构型2与构型5的弯曲刚度参数一致;构型3 在0◦方向弯曲刚度参数较小。由此可见,当以0◦为主方向设计时,构型1 和构型4 的弯曲刚度参数较大,在相同尺寸和边界条件下,屈曲稳定性承载能力较强,且优于原构型;构型2、构型3、构型5 弯曲刚度参数相对较小,其屈曲稳定性承载能力相对较弱。考虑壁板表层结构损伤容限设计,通常将±45◦放在表层,构型1 的铺层方式较好,尤其是以局部屈曲为临界载荷设计的壁板,仅需要调整铺层顺序不增加重量即可满足稳定性需要。
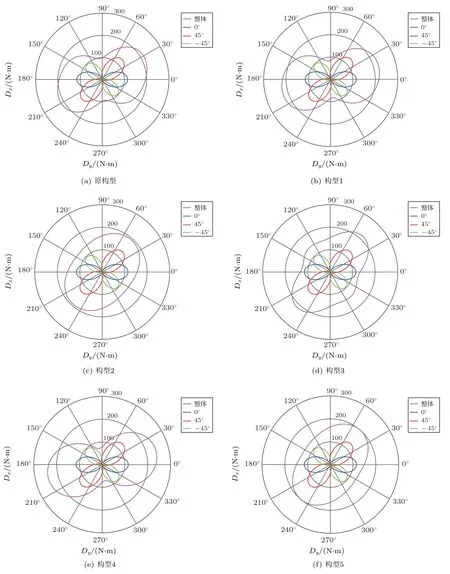
图4 单向铺层(0◦,±45◦)和不同铺层构型的复材整体结构弯曲刚度参数Fig.4 The bending stiffness parameters for a single plies of laminate (0◦,±45◦) and the full skin with different configuration

图5 不同铺层构型的复材整体结构弯曲刚度矩阵系数DijFig.5 The Dij bending stiffness for the full skin with different configuration
3 复材结构隔声性能分析
根据第3 节的分析,发现构型1、构型4 与原构型弯曲刚度特性一致,构型2、构型3、构型5 与原构型弯曲刚度特性差别较大。其他研究表明,与金属壁板结构相比,复材壁板在中高频上的隔声性能明显下降。鉴于此,非常有必要对复材结构的声学性能加以研究,以尽可能地获得最佳的隔声效果,并且在复材结构的设计中要综合考虑结构布局、铺层形式以及声学性能的影响,进行最优参数化设计。本节首先利用SEA 法对复材结构进行建模,对比不同的噪声处理方式下复材结构的隔声性能,并与测试结果进行对比,验证建立的SEA 模型。然后在验证的SEA 模型上,对表1 中的不同铺层构型的复材结构隔声性能进行分析,确定层压板的铺层角度、顺序对结构声学特性的影响,最终达到最优参数化设计的目的。
复材结构隔声测试在混响室-消声室进行,采用声强法测试,被测结构通过铝合金重型双层结构的框架安装到测试窗口上,侧边采用带加强框架的厚铝板,以及定制的异形高碳钢结构和框架连接,可以有效约束蒙皮的法向振动充分实现固支边界条件,见图6。结构与框架间利用M8-M12规格、A2-70或以上的不锈钢螺栓固定,螺栓间距为0.5 m。隔声测试时,以两个放置于混响室角落的大功率全频扬声器系统作为发声器,频率范围40 Hz∼6 kHz 的白噪声信号作为激励,利用声强扫描法采集测量面的法向声强级,并计算出壁板的隔声量。复材结构的阻尼损耗因子分别采用力锤法和稳态激振器法测试获得,随机在51 个激励点进行激励,板上布置42 个加速度计采集振动响应,计算平均均方振速,见图7。测试得到的复材结构固支边界条件下的阻尼损耗因子见图8。从图8 中可以看出,复材结构在200 Hz 以上频段的阻尼损耗因子在2%左右,且两种不同激励下测试结果吻合性较好。

图6 复材结构隔声测试安装图Fig.6 The installation of the composite curved skin on the TL test

图7 复材结构阻尼测试安装图Fig.7 The installation of the composite curved skin on the damping test

图8 复材结构阻尼损耗因子Fig.8 The damping loss factor of the composite curved skin
在VA One 软件中,利用Orthotropic Solid 对结构进行建模,并在结构两侧分别建立声空间子系统模拟发声室和接收室,利用扩散声场激励,如图9所示。阻尼损耗因子来自于图8的测试数据。在VA One 软件中计算SEA 模型的隔声量,并与3 种不同声学处理方式下(见表2)复材结构的隔声量1/3 倍频程测试结果进行对比,如图10(a)所示。可以看出,工况2 和工况3 仿真结果与测试结果吻合较好;工况1在2000 Hz 以上仿真结果与测试结果吻合较好,但在1000 Hz、1250 Hz、1600 Hz 三个频率上,工况1 的仿真结果与测试结果误差较大,分别达到8 dB、11 dB、10 dB,其余频率上基本在±5 dB 范围内,如图10(b)所示。这是因为工况1 是光壁板状态,环频率fr和吻合效应频率fc在仿真中的影响很明显,但在测试中受安装状态的影响,这两个频率不突显。

图9 复材曲板结构传声损失SEA 模型Fig.9 The SEA model of the composite curved skin
此外,对复材壁板采取声学处理之后,整体结构的隔声量明显提高。尤其是在壁板表面铺设127 mm、9.6 kg/m3的隔音棉之后,整体结构在500 Hz 以上频率隔声量提高显著15 dB 以上;在此基础上,增加内饰板安装之后,整体结构的隔声量在整个频段上又能提高5∼10 dB。由此可见,为提高复材壁板的隔声性能,有必要铺设一定厚度的隔音棉。

表2 不同声学处理方式的复材结构Table 2 The composite skins with different noise control treatment

图10 不同声学处理方式的复材结构隔声量仿真与测试结果对比(1/3 倍频程)Fig.10 TL comparison of the composite skins with different NCT between simulation and measurement data (one third octave)
利用SEA,分别对表1 中的构型1∼构型5 等不同铺层构型的复材结构进行隔声性能评估,并与原构型进行对比,在表2 不同工况下分析铺层顺序对结构隔声特性的影响,如图11 所示。可以看出,因铺层顺序对层压板弯曲刚度的影响,导致构型2的吻合效应频率fc比其他构型小,因此构型2 的隔声性能在吻合效应区域相对于其他构型较差;构型1 与构型4 隔声效果最好,但构型4 中表层非±45◦;而其余构型的隔声性能与原构型相比差别不大。因此,在进行复材结构设计时,应考虑铺层顺序对结构隔声性能的影响,综合刚度设计需求,构型1的铺层方式为最优。

图11 不同铺层构型的复材结构隔声量对比Fig.11 TL comparison of the curved panels with different configurations
4 复材结构参数优化设计
通过以上分析,发现铺层角度对结构的弯曲刚度和隔声性能有明显影响,且复材壁板的隔声性能在整个频段内都不高,在机身结构设计时,除了综合考虑铺层角度的影响之外,还需对复材壁板进行声学处理,铺设合适厚度和密度的隔音棉。受工艺和强度的影响,铺层角度可选择的铺设构型有限,为达到更好的声学效果,必须在声学处理上进行参数优化设计。本节以铺设在复材壁板上的隔音棉厚度和密度为两个优化参数,进行最优化分析,寻找最佳组合方式。
考虑目前航空用的隔音棉材料密度一般从5 kg/m3到24 kg/m3不等,在机身壁板与内饰板之间可以铺设隔音棉的空间从40 mm 到130 mm 不等,在此选择范围内进行SEA 参数优化。为更好地对比优化结果,以工况1的隔声量为参考基准,分析工况2中不同参数下的隔音棉插入损失,以及工况3下不同参数下的隔音棉与内饰板(内饰板参数不变)组合结构的插入损失,两种工况下的分析结果见图12、图13 所示。从图12 中可以看出,工况2 下的隔音棉密度对插入损失影响较小,因此从重量成本考虑可以选取较轻的隔音棉进行铺设;而隔音棉厚度对插入损失影响较大。从图13 中可以看出,工况3下的隔音棉密度对插入损失影响较小,与工况2下的结论一致;而隔音棉厚度对插入损失在1000 Hz以下频段影响较大,1000 Hz 以上改变隔音棉密度对插入损失基本无影响,因此为保证低频的隔声效果,考虑重量成本,可以选择合适的隔音棉的厚度,以达到最佳的效果。
为更好地说明隔音棉最优化的参数选取,以630 Hz(环频率)和2000 Hz(吻合效应频率)这两个频率为优化对象,分别绘制工况3 在不同密度和不同厚度下的隔声量,如图14 所示,发现工况中已经选取的隔音棉密度9.6 kg/m3和厚度127 mm 已经使工况3 的隔声量达到了收敛状态,因此本文中选取的隔音棉参数合理,可以作为优化设计的依据。
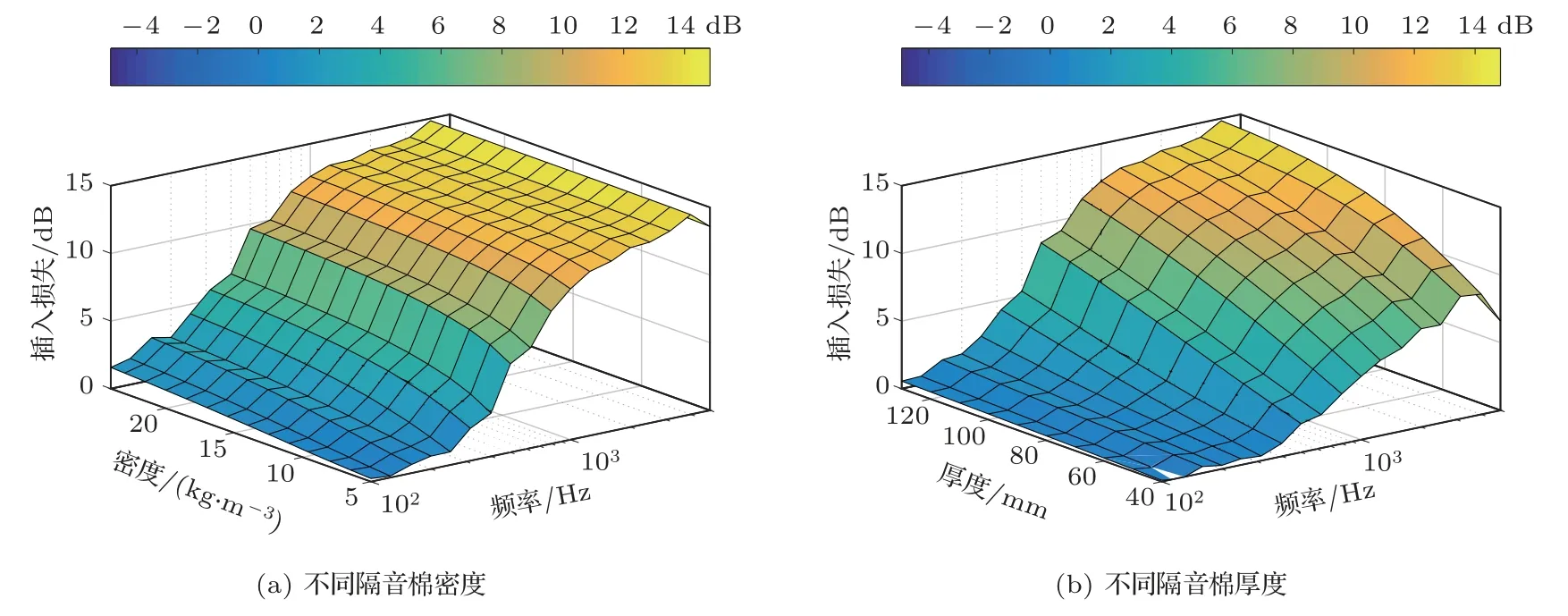
图12 隔音棉插入损失仿真结果(工况2)Fig.12 The simulation results of the insertion loss of insulation blanket (case 2)
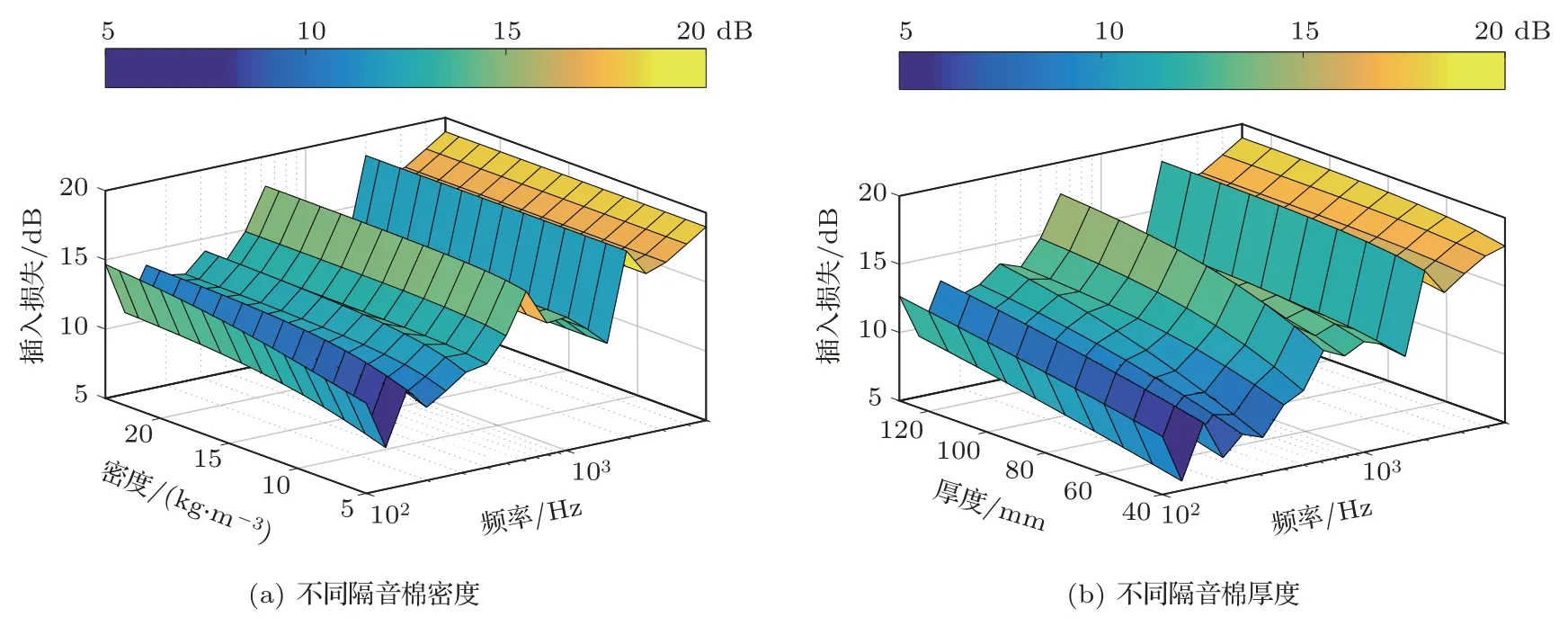
图13 隔音棉+内饰板插入损失仿真结果(工况3)Fig.13 The simulation results of the insertion loss of insulation blanket (case 3)

图14 工况3 的隔音棉参数优化Fig.14 The optimization of insulation blanket in the case 3
5 结论
综上所述,在总铺层数和铺层比例不变的前提下,分析不同铺层构型对结构件刚度的影响。通过对5 种不同铺层顺序的构型进行分析,对比复材整体结构弯曲刚度,以及刚度矩阵系数在极坐标下的分布,得出结论:不同铺设角度顺序对复材整体结构的弯曲刚度有影响,且呈现出对称且弱耦合性;构型1 和构型4 的弯曲刚度参数与原构型类似;构型2 与构型5 的弯曲刚度参数一致;构型3 在0◦方向弯曲刚度参数较小。在复材结构设计中,当以0◦为主方向设计时,且考虑壁板表层结构损伤容限设计,在相同尺寸和边界条件下,构型1 屈曲稳定性承载能力较强,铺层方式较好。
利用SEA 法,进一步对这5 种不同构型的复材结构进行隔声性能分析,得出结论:不同铺设角度顺序对复材整体结构的吻合效应频率有影响;构型2 的吻合效应频率比其他构型小,因此构型2 的隔声性能在吻合效应区域相对于其他构型较差;构型1 与构型4 隔声效果最好,但构型4 中表层非±45◦;而其余构型的隔声性能与原构型相比差别不大。因此,在进行复材结构零件设计时,应考虑铺层顺序对零件隔声特性的影响,综合刚度设计需求,构型1的铺层方式为最优。
最后,由于复材壁板的隔声性能在整个频段都不高,在机身结构设计时,需对复材壁板进行声学处理,铺设合适厚度和密度的隔音棉。通过分析铺设在复材壁板上的隔音棉厚度和密度两个参数,得出结论:隔音棉密度对插入损失影响较小,因此从重量成本考虑可以选取较轻的隔音棉进行铺设;而隔音棉厚度对插入损失影响较大,因此为保证隔声效果,考虑重量成本,可以选择合适的隔音棉的厚度,以达到最佳的效果。经过对630 Hz (环频率)和2000 Hz(吻合效应频率)这两个频率的优化分析,本文选取的隔音棉密度9.6 kg/m3和厚度127 mm 已经使壁板、隔音棉及内饰板的组合结构隔声量达到了收敛状态,是最优化的组合设计。

