两种方法巧解“水池排水时间”问题

张 伟

(重庆市万州高级中学 重庆 404120)

【例题】如图1所示，一底面积为S，高为H的圆柱形水池装满水(视作理想流体)，在水池底部侧面有一横截面积为S0(S0≪S)的小孔(小孔的线度远小于H)，在只考虑重力的情况下，求水全部流完所需要的时间.(已知重力加速度为g)

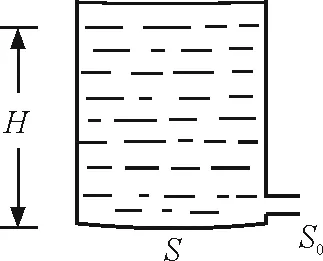
图1 例题题图

1 竞赛层面 用伯努利方程和微积分的方法

由于水从小孔流出导致液面下降，设液面下降的速度为v1,从小孔中流出水的速度为v2(如图2)，由于液体不可压缩，在一个极短的时间Δt内满足

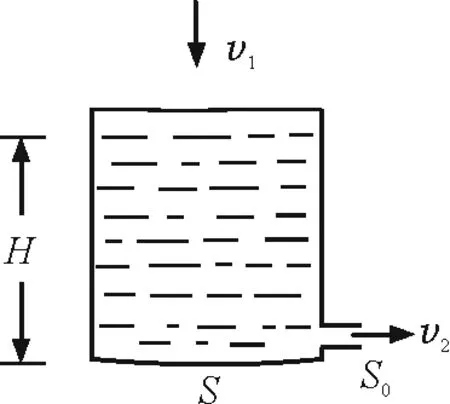
图2 例题微积分法求解分析

v1ΔtS=v2S0Δt

(1)

解得

(2)

选择小孔处为零势能面，某一时刻液面到小孔的高度为h，由伯努利方程得[1]

(3)

式(3)中，P0表示大气压，ρ表示水的密度.

由于S0≪S，式(2)中v1近似等于零，则可通过式(3)解得

(4)

设在dt时间内，液面高度变化(末态高度与初始高度的差值)为dh(dh<0)，由于液体不可压缩，则

-Sdh=S0v2dt

(5)

将式(4)代入式(5)，得

(6)

对式(6)两边同时积分，得

(7)

得

(8)

解得

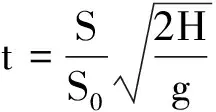
2 高考层面 运用能量守恒和平均值法巧解

由前面式(1)、式(2)和S0≪S，得v1近似等于零，可认为在极短的时间Δt内，液面下降的高度Δh≪h，液面处质量为Δm的一层很薄的水层(如图3)下降时具有的动能为零.

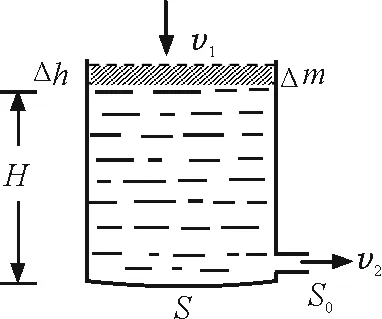
图3 例题能量守恒法求解分析

根据能量守恒定律，液面下降时薄水层减少的重力势能应该转化为从小孔流出去时水的动能，即

(9)

解得

(10)

式(10)表明，水从小孔流出的速度和物体从高h处做自由落体运动的末速度是一样的.

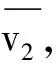
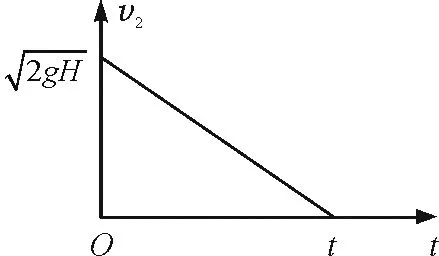
图4 v2-t图

(11)

由于液体不可压缩，可得

(12)

将式(11)代入式(12)，解得

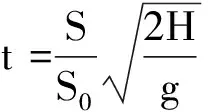
3 结束语

本文分别从伯努利方程和能量守恒、平均值法来巧解“水池排水时间”的问题[2].在物理教学中，多和学生进行这样的分析讨论，无论对于提升学生的理论水平、分析能力，还是对于提升学生物理学习的兴趣，都能起到较大的推动作用.