对毕奥-萨伐尔定律建立过程中的一种分析方法

杨胜云 苏立波

(兴义民族师范学院物理与工程技术学院 贵州 黔西南 562400)

1 引言

1820年奥斯特发现电流的磁效应[1]，开辟了电与磁之间的联系，促进了电磁学的开端.奥斯特本人对他的发现只做了定性的研究，定量规律则是由毕奥与萨伐尔师生两人建立的.他们为了得到电流磁效应的定量表达式，设计了两个精巧实验[2，3]，实验的最终目的是得到电流元对某点磁极的作用力，由于不存在孤立的电流元，使得实验无法直接测量，于是他们请来拉普拉斯做数学分析[4].对于毕奥-萨伐尔定律建立过程中的实验以及数学分析，教材中基本不做介绍，文献[5，6]给出了证明方法，但这种证明方法不太适合初学者了解.在文献[7]中给出类似于拉普拉斯的分析方法，该分析过程比较繁杂，为此本文将给出另一种分析方法，以较为简洁的过程得到此定律.

2 毕奥-萨伐尔定律建立的分析过程

毕奥与萨伐尔设计的第二个实验中，已经得到弯折载流导线对导线外P点的磁极作用力表达式，实验原理如图1所示.

图1 毕奥与萨伐尔的第二个实验示意图

按照图1的实验，毕奥得到弯折载流导线对P点的磁极作用力的表达式为

(1)

式(1)中I为电流，k为比例系数，由于整条弯折载流导线对P点的磁极作用力垂直纸面向里，所以理所当然地假定每个电流元Idl对P点的磁极作用力也垂直纸面向里，则载流导线对P点的作用力应为电流元对P点作用力在导线上的积分，即

(2)

式(2)中的L为弯折载流导线，由于弯折导线关于虚线对称，所以式(2)等号左边的积分可以分解为虚线上半部分积分的两倍，即

(3)

图1中的几何分析如图2所示.

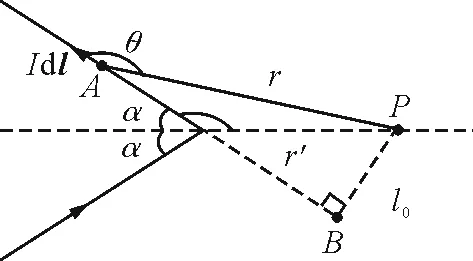
图2 弯折载流导线对P点磁极作用力分析图

图2中，电流元Idl的尾端所在位置设为A点，B点为电流元Idl的反向延长线上的一点，PB⊥AB,△ABP为直角三角形，设AB边长为l.由图2中r与θ确定了电流元Idl与P点的位置关系，则每个电流元对P点贡献的磁极作用力dF必然是r与θ的函数，令dF中r,θ的函数为H(r,θ)，由等式(2)的关系可得dF正比于电流I，据磁场和力的叠加原理，dF还与电流元长度dl成正比，则

dF=H(r,θ)Idl

(4)

将式(4)代入式(3)中得

(5)

式(5)中只含有未知函数H(r,θ)，r,θ都是变量，需要统一积分变量，由图2中的几何关系得

(6)

由式(6)得

dl=l0csc2θdθ

(7)

将式(6)和式(7)代入式(5)得

(8)

由于较远处的电流元对P点的影响非常小，假定导线两端无限长，所以θ的积分区间为(π-α)→π.由图2和式(6)可得θ取(π-α)时r′=r，把r代入式(8)得

(9)

式(9)等号两边中的l0，严格意义上它是α和r′的函数，这里为了方便运算，令l0为定值，这样规定并不影响结果.则式(9)的等号两边只是α的函数，等号两边同时对α求导得

(10)

式(10)中将等号左边的未知函数的两个变量分别用r,θ代换，即

(11)

将式(11)代入式(10)得

(12)

将式(12)的H(r,θ)函数代入式(4)得

(13)

再考虑矢量因素，则式(13)改为

(14)

3 总结

毕奥与萨伐尔设计了两个特殊实验，却能够在从中经过以上严格数学分析得到一般结论，可见毕奥与萨伐尔设计实验的巧妙性.但分析过程并非很容易就可以得到，单从数学的角度看，只是从积分的结果求解微分的过程，由于几何关系的繁杂，增加了分析过程的难度.为此本文给出严格的数学分析方法，并在分析过程中追求方法的简洁，最终以较为简洁的方法得到此定律，由此可见数学分析对物理定律建立过程中的重要意义.