基于STK 的航天器轨道动力学仿真教学方法研究

王卫杰，张雅声，任 元，姚 红，刘 通

（1.航天工程大学 宇航科学与技术系，北京 101416；2.航天工程大学 航天指挥学院，北京 101416）

航天器轨道动力学（orbital dynamics）是以高等数学、牛顿力学、控制理论为基础研究航天器轨道（或质心）运动理论和轨道应用的科学。航天器轨道即航天器质心的运动轨迹。自1957 年第一颗人造地球卫星发射成功以来，航天器轨道动力学逐步发展成为与工程实践密切相关的应用学科。

我校致力于培养航天指挥管理与工程技术人才，航天器轨道动力学是我校航天本科专业和航空宇航科学与技术学科研究生必修的专业课。学习该课程既要有扎实的数学力学等相关先修基础知识，也需要有跳出地球看宇宙的空间逻辑思维想象力。对于习惯以地球为宇宙时空中心的初学者，面对浩瀚的数学公式，多种时空参数的交替转化，如何调动学生的学习积极性，保证良好的课堂教学质量，是主讲教师必须思考的问题。

1 STK 软件及其应用

仿真实验实践教学有利于引导学生探究性学习，提高教学效果[1-2]，是当前教学模式改革方向之一，航天动力学仿真软件是航天动力学理论与工程实践联通的桥梁。目前最为成熟的航天任务仿真分析商业软件当属美国AGI 公司开发的STK。其原名为卫星工具包，具有复杂实体建模、优异仿真分析、强大交互式图文输出、可靠计算结果和极强扩展性等功能和特点[3]。在课堂教学中，STK 可将抽象的教学内容可视化，拓展学生的实践技能，加深对所学知识的应用理解。文献[4]针对航天装备教学中存在的教学手段单调和实践环节不足等问题，基于STK 给出了地球静止轨道（GEO）摄动仿真的实验教学案例。文献[5—6]分别将STK 引入天体力学和航天测控课堂教学，给出了基于STK 的复杂坐标演示和简单轨道模拟等仿真实例。文献[7—9]针对卫星导航系统教学仿真需求，引入STK 辅助课程教学，制作了基于STK 的北斗导航卫星星座地面覆盖性能应用案例。文献[10—11]采用STK制作了航天器的轨道预报和卫星星座仿真实例。文献[12]探讨了STK 在作战模拟与仿真课程教学中的应用。上述研究结合自身教学需求从不同侧面应用了STK 仿真功能，但在课程分析和学生实践参与度方面仍需加强。

基于上述分析，本文针对航天器轨道动力学课程理论性和应用性强的特点，研究基于STK 的课程仿真实验实践教学方法。结合学生学情，以问题为导向，明晰课程教学目标，梳理课程内容体系，提出基于仿真场景课件和仿真实验课程设计的教学改革思路。分析了基于STK 的课程教学仿真课件和实验设计教学模式，提炼出航天器轨道机动设计和地面覆盖能力分析两个课程设计题目。选取经典霍曼转移轨道，基于STK/Astrogator 模块给出了轨道机动设计的仿真实例。

2 航天器轨道动力学课程分析

2.1 教学目标

航天器轨道动力学课程以天体力学及基本控制理论知识体系为依据，围绕航天器轨道运动理论及其应用开展教学。课程通常开设于本科第7 学期，学生已完成相关基础理论课学习，进入专业技能学习阶段，希望通过学习将抽象的数学力学问题具体化、实践化。通过本课程学习，应让学生明晰以下问题：

（1）作为人造天体，航天器运行在什么样的时空环境？涉及哪些坐标系？

（2）什么是航天器轨道，轨道运行有哪些特点，如何进行描述？何为开普勒根数？

（3）航天器运动受哪些作用力影响？何为摄动力？

（4）航天器如何保持或抵达目标轨道？如何根据任务需要调整轨道？何为轨道机动？

（5）如何设计航天器轨道，使其更好地为人类服务，典型轨道有哪些？

这些问题构成了本课程的主要内容，也是本课程教学的重点、难点。

2.2 课程内容体系

航天器轨道动力学是在经典天体力学的基础上发展而来的，经典天体力学在研究自然界天体运动的过程中总结出轨道摄动理论。航天器具有自然天体的一般运动规律，区别在于轨道可以人为选择并加以控制，使命任务是为人类提供探测、导航、通信和科学实验等轨道应用功能，因此航天器轨道动力学课程内容包括轨道运动理论和轨道应用两大部分，如图1 所示。

图1 航天器轨道动力学课程内容体系

轨道运动理论研究的目的在于精确地求出航天器在任意时刻、给定坐标下的位置、速度。涉及的坐标系主要有地球惯性坐标系（地惯系）、地心固连坐标系（地固系）和轨道坐标系等。轨道运动以摄动理论为基础，将航天器轨道分为符合二体问题运动规律的开普勒轨道，即理想轨道，以及实际轨道与理想轨道的差，即轨道摄动。求解轨道摄动的方法有近似解析法（普遍摄动法）和数值积分法（特别摄动法）。

轨道应用研究以轨道运动理论为基础，应用类型可分为对地信息支援、在轨操控以及深空探测等三个方面。其中对地信息支援涉及航天器与地面的相对运动，是目前最主要的轨道应用类型。本课程轨道应用教学主要围绕对地信息支援展开，内容包括轨道机动、轨道设计、典型轨道等。轨道机动是在航天器运动过程中施加控制力以保持或改变原来的轨道；轨道设计是根据航天器担负的使命论证选择最有利的运行轨道；业已设计且实际应用的典型轨道主要有地球静止卫星轨道、回归轨道、太阳同步轨道、冻结轨道等。

2.3 教学改革思路

基于上述分析，航天器轨道动力学课程具有理论性和工程应用性强的特点。为了调动学生课堂学习积极性，发挥课下主观能动性，围绕课程教学目标和内容体系，借鉴国内相关课程的教学改革方法和实践经验，结合笔者近些年本课程教学体会，认为应增强轨道理论的形象化和轨道应用的实践化，并提出基于STK 的仿真场景课件和仿真课程实验的教学改革思路。

3 基于STK 的仿真教学模式

航天器轨道动力学教学中的STK 仿真教学包括两种教学模式：理论教学中基于STK 的仿真场景课件制作；实践教学中基于STK 的仿真实验课程设计。

3.1 仿真场景课件制作

轨道理论难以像基础教学那样去层层推导数学公式，且许多公式本身也无法用解析的方式给出推导过程，如开普勒轨道方程的求解。同时，对于航天器运行的空间时空关系，也很难用语言或手绘图形表述，因此将STK 仿真场景作为课件要素引入教学十分必要。

仿真场景课件利用STK/VO 模块2D/3D 可视化场景，可将复杂抽象的轨道动力学理论知识以平面/立体的图片/视频形式直观展现出来。以讲授航天器轨道和坐标系的相关内容为例，制作3D 仿真场景视频，如图2 所示。场景参考系设置为地惯系（红色坐标轴），播放场景后，地惯系和航天器轨道（黑色椭圆）保持不变，地固系（黑色坐标轴）随地球自转，航天器则在轨道上运行。通过仿真场景，对动静坐标系、航天器轨道稳定性和航天器位置时变性之间的关系一目了然。

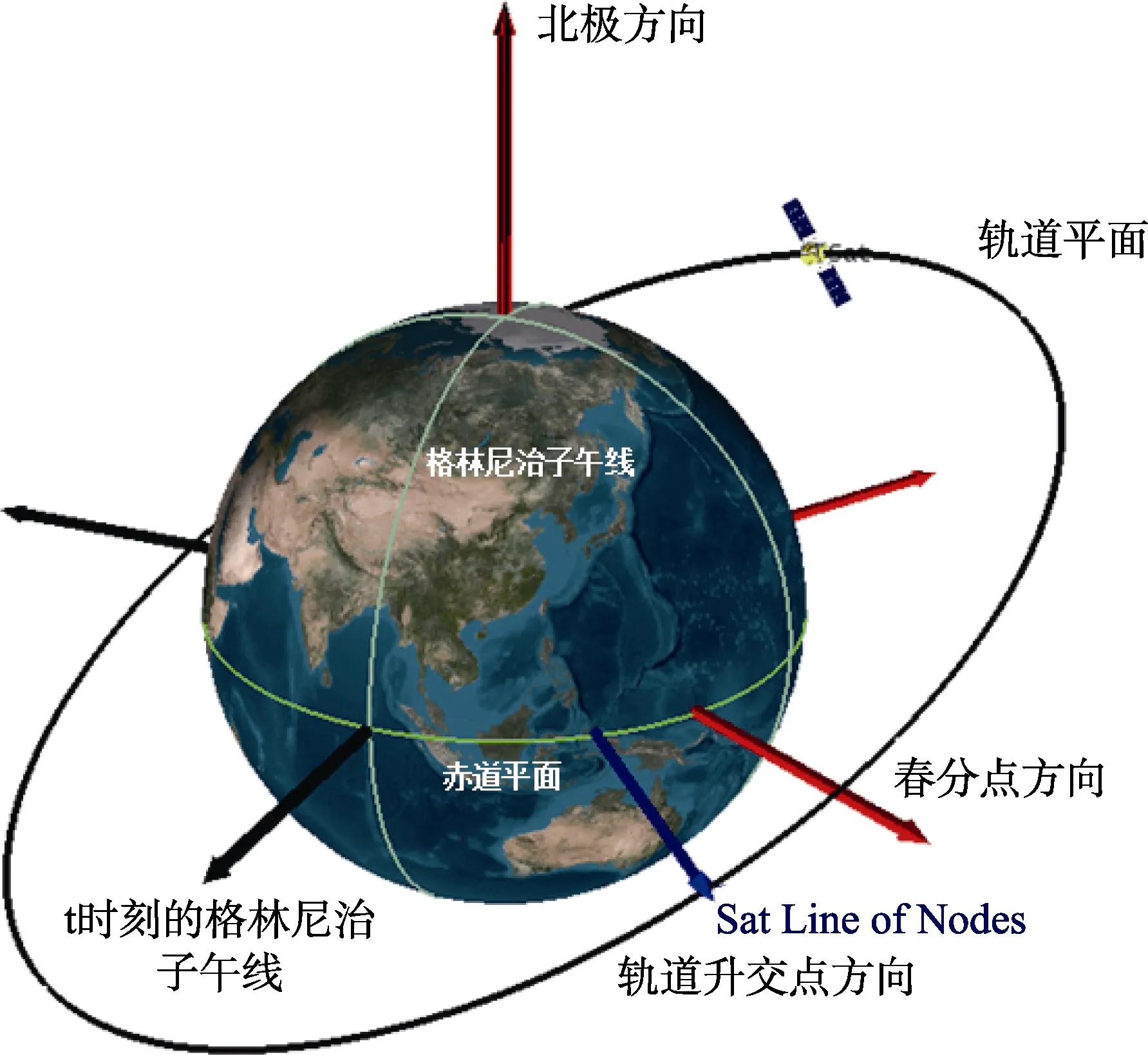
图2 坐标系及航天器的轨道运动

3.2 仿真实验课程设计

结合轨道理论知识，围绕轨道工程应用，设计了STK 仿真实验题目，让学生动手分析轨道摄动影响，面对具体任务设计轨道，通过轨道机动达成目标轨道，基于应用需求明晰航天器对地覆盖性能等，培养提高学生航天素质。并通过量化的图表报告，使学生学会运用相关航天理论和规律分析航天器轨道性能指标，为学生胜任航天指挥和工程应用岗位需求奠定基础，突出课程的实战化教学导向。

考虑本课程包括轨道运动理论和轨道应用两大模块，轨道运动理论是轨道应用的基础，因此轨道应用仿真实验设计也是对学员所学轨道运动理论的综合应用。在轨道应用部分，轨道机动和轨道设计紧密相连，轨道机动是实现所设计轨道的途径，轨道设计则围绕航天器与地面的相对运动关系，聚焦星下点轨迹和地面覆盖分析。

基于上述分析，在教学中提炼出两个仿真实验课程设计案例：①基于STK/Astrogator 模块的航天器轨道机动设计；②基于STK/Coverage 覆盖模块的航天器地面覆盖能力分析。

下面给出基于STK/Astrogator 的航天器轨道机动设计仿真实验应用实例。

4 课程设计应用实例

4.1 STK/Astrogator 模块

STK/Astrogator 是交互式轨道机动和轨道设计的专用分析模块，用于高精度轨道机动设计仿真分析，其页面如图3 所示。

图3 STK/Astrogator 模块页面

STK/Astrogator 通过用户定义的任务控制序列（mission control sequence，MCS）来计算航天器星历及执行程序飞行任务，从而实现航天器沿预定轨道运行。作为一种图形编程语言，MCS 以任务段（mission segments）的形式规定如何计算航天器轨道。任务段分为星历生成段和程序控制段两大类。

星历生成段顾名思义用于生成不同飞行任务的航天器星历，共分为7 种：①初始状态段（Initial State），用来定义MCS 航天器根数、质量、燃料等初始条件；②发射段（Launch），用于模拟从地球或其他天体发射航天器；③跟随段（Follow），用于模拟子航天器在给定位置伴随主航天器飞行；④机动段（Maneuver），用来设定发动机点火进行轨道机动，一种为“脉冲模型”（Impulsive）模式，另一种为“有限推力模型”（Finite）模式；⑤外推段（Propagate），用来将卫星的轨道按照选定的力模型进行轨道外推计算，采用的轨道预报器为HPOP；⑥保持段（Hold），用于模拟交会对接操作中航天器位置的保持；⑦更新段（Update），用于修改航天器属性和用户变量，反映任务期间发生的变化。

程序控制段用于控制MCS 任务的执行顺序，分为5 种：①序列段（Sequence），组织包含任意段构成系列段，可通过Scripting Tool 脚本工具使对象属性、对象组件和自定义参数进行交互；②反向序列段（Backward Sequence），与序列段类似，不同处是按照时间相反的方向进行，通常用来在已知条件下反推之前的状态；③目标序列段（Target Sequence），相比序列段增加了2 类搜索配置文件和7 类段配置文件，其中搜索文件“微分修正器（Differential Corrector）”利用微分校正算法，根据约束量自动调整自变量的值，直至满足需求；④返回段（Return），用来返回到其父段；⑤终止段（Stop），用来控制是否终止MCS运行。

在轨道机动设计仿真中，上述各段按照设定顺序排列，STK 每计算完一段后，保存各种状态量，并作为下一段的初始值，进行下一段计算，直至结束。

4.2 霍曼转移仿真实验

霍曼转移是轨道机动教学的经典内容之一。霍曼转移轨道（Hohmann transfer orbit）是两次冲量的最优转移，是针对同心共面、半径不同的两圆轨道之间的转移，可用于实现航天器交会对接[13]，其过程原理如图4 所示。在半径为1r 的圆轨道1C 上的任意点，施加速度冲量Δ1v，进入椭圆转移轨道E，该点即为轨道E的近地点，在E 的远地点施加速度冲量Δ2v，进入半径为2r 的圆轨道C2。

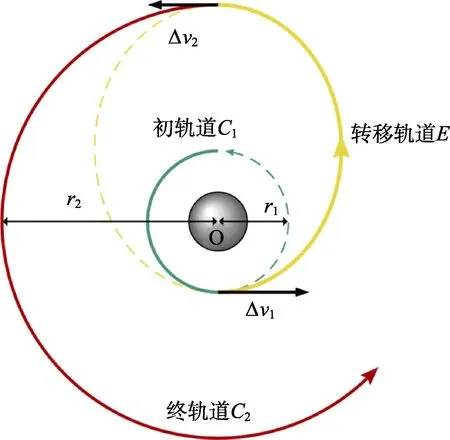
图4 霍曼转移示意图

仿真实验中，1r =6 878 km，2r = 42 164 km，即初轨道为高度500 km 的近地轨道，终轨道为地球静止轨道（GEO）。对1C、 C2、E 轨道分别运用活力公式，即：

式中，v 为航天器速度，μ 为地球引力常数，r 为航天器与地心的距离，a 为轨道半长轴。

可得 v1=7.61 km/s，v2=3.07 km/s，Δ v1= 2.37 km/s，= 1.44 km/s。

依据上述参数，结合图4 所示转移过程，基于STKK/Astrogator 定义霍曼轨道转移仿真MCS，如图5所示，共用到了5 个任务段。

图5 霍曼转移MCS

仿真流程如下：

步骤1：利用Initial State 段在地惯系笛卡尔坐标中设置初轨道参数。

步骤2：利用Propagate 段设置航天器在1C 轨道上的运行时间，其中轨道预报器选用HPOP，终止条件为远地点Apoapsis。

步骤 3：利用 Target_Sequence1 及其包含的Maneuver 和Propagate 段仿真实现航天器第一次冲量变轨。首先在Maneuver 中将机动类型设置为冲量型Impulsive，选中X 轴分量施加速度冲量，此变量将被作为搜索文件的控制参数（control parameters）。其次，在 Propagate 段中通过“Results…”选项添加变量Altitude Of Apoapsis，作为搜索文件中的等式约束量（equality constraints）。最后，在Target_Sequence1 中配置搜索文件Differential Corrector，将速度冲量修正值Correction 设置为2.37 km/s；将转移轨道远地点期望高度设置为35 286 km，如图6 所示。

步骤4：与步骤3 类似，利用Target_Sequence2实现航天器第二次冲量变轨，与第一次变轨不同之处是，速度冲量修正值为1.44 km/s，等式约束量为偏心率Eccentricity，因终轨道为地球静止轨道，故偏心率期望值设为0。

图6 Differential Corrector 搜索文件页面

基于上述仿真流程，点击运行MCS，最终实现霍曼转移仿真实验案例，如图7 所示。图中坐标为地惯系，绿色轨迹为初轨道，蓝色轨迹为转移轨道，黑色轨迹为终轨道。对于仿真过程的具体分析报告，可通过Astrogator 模块的Summary 查看。

图7 霍曼转移仿真实现图

5 结语

针对航天器轨道动力学课程理论性和应用性强的特点，研究了基于STK 的课程仿真实验教学方法。结合学生情况，以问题为导向，明晰课程教学目标，梳理课程内容体系，提出了基于仿真场景课件和仿真实验课程设计的教学改革思路，提炼出航天器轨道机动设计和地面覆盖能力分析两个课程设计题目。选取经典霍曼转移轨道，基于STK/Astrogator 模块给出了轨道机动设计的仿真实验实例。教学实践表明，该方法有利于学生构建空间逻辑思维、理解复杂理论问题、培育实践应用能力，有效提升了教学效果。