跨音速风洞翼型试验与数值仿真应用

马震宇，王正鹤，赵希玮，程兰兰

（1.郑州航空工业管理学院 航空工程学院，河南 郑州 450046；2.空军工程大学 航空工程研究生队，陕西 西安 710038；3.西北工业大学 动力与能源学院，陕西 西安 710072）

计算机技术在力学实验教学和培养学生实践能力中的作用日显重要[1-4]。翼型或叶型风洞物理试验是针对翼型在风洞试验段中所进行的二元化模型流场和气动力吹风测量，是分析和改进飞行器和叶轮机等升力面部件气动力性能的基础。航空先进国家都对翼型和叶型展开了大量的设计方法与风洞测试研究，积累了丰富的和系列化的数据库资源[5-7]。

借助计算机和数值计算方法的流动数值仿真技术能够与理论模型分析和风洞模型物理试验相互校验、补充和促进，而且通过流动数值仿真技术，不仅可以了解问题和现象的结果，还可以随时动态或连续重复地可视化流场特征，有助于认识和掌握复杂流动整体与局部的细致过程。王科雷等[8]以高空长航时无人机翼型为对象，对超临界翼型RAE2822 在飞行马赫数0.75 和雷诺数6×105～6×106条件下的低雷诺数跨音速气动特性进行了数值仿真计算与优化，采用SST k-ω湍流模型，可视化呈现了翼型表面时均紊流流线分布与激波和流动分离，较详细地分析了压强系数分布和升阻力变化特性。关键和郭正[9]以翼型E387（E）为对象，应用SST k-ω 湍流模型对雷诺数为3×105的不可压低雷诺数翼型绕流进行数值仿真计算，可视化呈现了翼型表面时均流线分布与分离泡和旋涡结构，并将升阻力系数随迎角变化的仿真结果与试验数据进行了比较分析。张强和杨永[10]数值模拟了绕翼型EPPLER387 的低雷诺数非定常流动，采用SST k-ω 湍流模型封闭雷诺时均N-S 方程组，可视化呈现了翼型表面计算流谱和分离泡结构，计算的时间平均升阻力系数和压力分布系数与实验数据符合良好。

不同线型和不同攻角状态的翼型和叶型具有不同的气动力特点，其流场流谱也不尽相同。流动数值仿真计算是数值风洞的核心[11-12]，但目前对风洞中试验模型流场进行数值仿真的研究[6,13-14]不仅数量少，而且缺乏深度和细节。本文以FL-1 风洞NACA0012翼型模型试验为研究对象，数值模拟亚跨音速试验的三维黏性流场，并与试验数据比较验证，可视化清晰呈现翼型周围网格分布、流线分布和局部激波结构等，有助于了解试验模型整体气动力和局部细节流动机理。

1 试验设备与模型试验

1.1 试验设备

FL-1 风洞[15]为半回流暂冲下吹式高速气流模拟地面设备，由低压（0.6 MPa）和中压（2.0 MPa）空气气源，与洞体及测控系统3 大部分组成。洞体部分主要由气流调压阀、稳定段、收敛段和喷管段、试验段（模型安装和测试区）、扩压段、引射段等组成。进行模型吹风试验时，测试数据采集与处理由洞体外监控系统自动完成。

风洞试验段横截面尺寸为600 mm×600 mm，长度为1.58 m。亚音速和跨音速试验来流马赫数调控范围为0.35～1.2（可连续调节），超音速试验来流马赫数最高可达4.0，控制精度为±0.003。试验压缩空气来流温控范围为263～305 K，总压控制在0.08～0.25 MPa 范围。在跨音速试验时，试验段左右壁为实直壁，上下壁为开闭比为15%的直孔壁板（孔径φ10 mm 均布），如图1 所示。模型攻角常规调节范围为±18°或0～36°，控制精度为±0.1°。

图1 FL-1 风洞试验段和翼型模型

1.2 试验模型和测压方法

试验对象为钢质二元机翼模型，翼剖面为NACA0012 对称翼型，其最大相对厚度位置距前缘相对距离为30%。模型弦长为100 mm（为试验段高度的1/6），展长为600 mm（展弦比为6），安装于风洞试验段左右侧壁之间，沿试验段前后和上下方向均处于居中位置，参见图1。沿展向距离模型前缘6%弦长位置，在模型表面上粘贴气流固定转捩薄条带（宽度2 mm）。在名义攻角3°时，模型迎风面积与试验段截面积之比即堵塞度，为0.87%。

模型中间剖面翼型保持二元绕流特性。从该剖面前缘向后缘按一定间隔开设23 个上表面静压测量孔（孔径φ 0.5 mm，且前6 个孔间隔距离分布相对密一些），以试验测量上表面绕流静压分布特性。各静压管从模型内部引出后穿过风洞侧壁与洞外应变式压力传感器相连，传感器测量精度为±0.3%。同时，为测定中间剖面不同表面点处沿法向流速分布特性，当地总压测量皮托管与移测架相连后一起装于试验段，参见图1，总压微型探头由外径φ 0.43 mm、内径φ 0.23 mm的毛细钢管制成。

在试验来流马赫数为0.8 时，基于模型弦长的特征雷诺数为1.64×106，可以认为模型流场属于低雷诺数范围[8,10]。

2 模型试验流场数值仿真

2.1 仿真状态和边界条件

应用CFD 方法对模型试验流场开展数值仿真，仿真条件与风洞模型实际试验状态一致，流场控制体边界按风洞试验段几何参数确定。模型试验流场具有以下力学模型特征：空间三维、可压缩空气介质、完全气体、定常、黏性流动、紊流、绝热壁面。试验段上、下开孔壁面按实壁简化处理。

流场边界条件类型设置中，进口截面采用压强远场条件（需设置来流马赫数和方向、相对操作压强而言的表静压、绝对静温、紊流度等参数值），出口截面为压强出口条件（需设置出流表静压、回流总温等参数值）。因来流相对模型侧滑角为零，故能够按半模型流场进行计算，在对称剖面上需要施加对称面等效边界条件。试验段左右实壁及模型表面均采用绝热固壁流动黏附无滑移边界条件。试验段上、下孔板壁面采用绝热固壁且壁面处气流切应力为零的边界条件，以近似模拟壁面开孔透气复杂效应。

2.2 流场结构化网格划分

采用应用广泛的ICEM CFD 软件[16]，对半模型流场流域进行六面体结构化网格划分。为了更准确地计算模型表面周围黏性流动大变化梯度参数，在模型表面周围沿当地法向生成15 层加密附面层网格（层间增长比为1.2），首层网格当地最大高度为0.001 mm，相应目标设定值Y+=4。在模型试验攻角3.05°时，流场流域网格划分结果为总单元数479.7 万、节点数469.4万，网格评价质量为正交性大于0.65、最小角度大于45°。网格品质优良，网格模型如图2 所示。

图2 流场结构化网格模型（试验攻角3.05°）

2.3 流动管控方程和仿真方法

在试验来流马赫数分别为0.5 和0.8、模型攻角3.05°、特征雷诺数1.64×106、模型前缘固定转捩条件下，按全湍流和完全气体模式，以雷诺时均化质量、动量和能量方程为流动管控方程（RANS），选择湍流封闭模型进行数值仿真。偏微分方程组离散方法为有限容积法[16]。

应用FLUENT 流动分析软件[16]，选择3D 和双精度模式，导入以上网格模型文件。选择基于密度和隐式算法，选择适应能力强的SST k-ω 为湍流补充模型，计算操作压强值设置为零。将所确定的边界类型条件具体化，根据进口预定马赫数和总压、总温选择值（可调）计算给出静压和静温，出口静压（背压）以试验有关值为参考上下可调，由此实时监视和调控进口平均马赫数以达到预定目标值。流率类型选用Roe 格式，方程对流迁移项离散采用二阶迎风格式，湍流动能和耗散率项为一阶迎风格式，亚松弛控制因子均设置为0.5。各方程项迭代计算收敛残差监控精度均设定为10-4，同时对模型升力和阻力系数进行迭代监控设定，对进口截面入流质量加权平均马赫数进行迭代监控设置。最后，设定流场特征参考值，初始化全流场，设置迭代步数，进行数值解算。

3 结果与分析

当各方程项迭代计算残差均达到和超过10-4时，观察模型升力和阻力系数也均趋于平稳，同时进口截面入流平均马赫数稳定于目标值，并且进口质量流率与出口质量流率保持平衡，表明数值计算迭代过程收敛到位。为了增强计算结果可视化效果，采用TECPLOT 软件[16]等进行数据后处理。

来流马赫数0.5 工况时，经过2 886 步迭代计算模型收敛，模型整体升力系数为0.363 9，阻力系数0.014 22。来流马赫数0.8 工况时，经过3 946 步迭代计算收敛，模型升力系数为0.175 9，阻力系数为0.047 04。模型表面流场Y+后处理值在0～4.76 之间分布，表明选用适应能力强的SST k-ω 为湍流补充模型是合适的[16]。

图3 为流场对称面处翼型绕流表面压强系数分布结果和比较。风洞试验来流马赫数为0.5 时，计算值与试验值全程吻合很好，流场为纯亚音速流动。来流马赫数增大至0.8 时，计算值与试验值变化趋势一致，吻合良好，流场为亚跨音速流动，在距翼型前缘35%弦长位置附近出现局部激波，从图4 的流场时均马赫数分布云图中能够清楚地看到计算捕获的激波。

图5 是对称面处翼型局部时均流场速度矢量分布云图。可见，激波出现使上表面主流速度由局部超音速迅速减慢，并诱导促使其后黏性附面层分离，这从图6 的翼型上表面壁面剪切应力分布曲线也能清楚看到。

图3 对称面处翼型表面绕流压强系数分布

图4 对称面处翼型流场时均马赫数分布（来流马赫数0.8）

图5 局部激波位置附近速度矢量分布（局部放大，来流马赫数0.8）

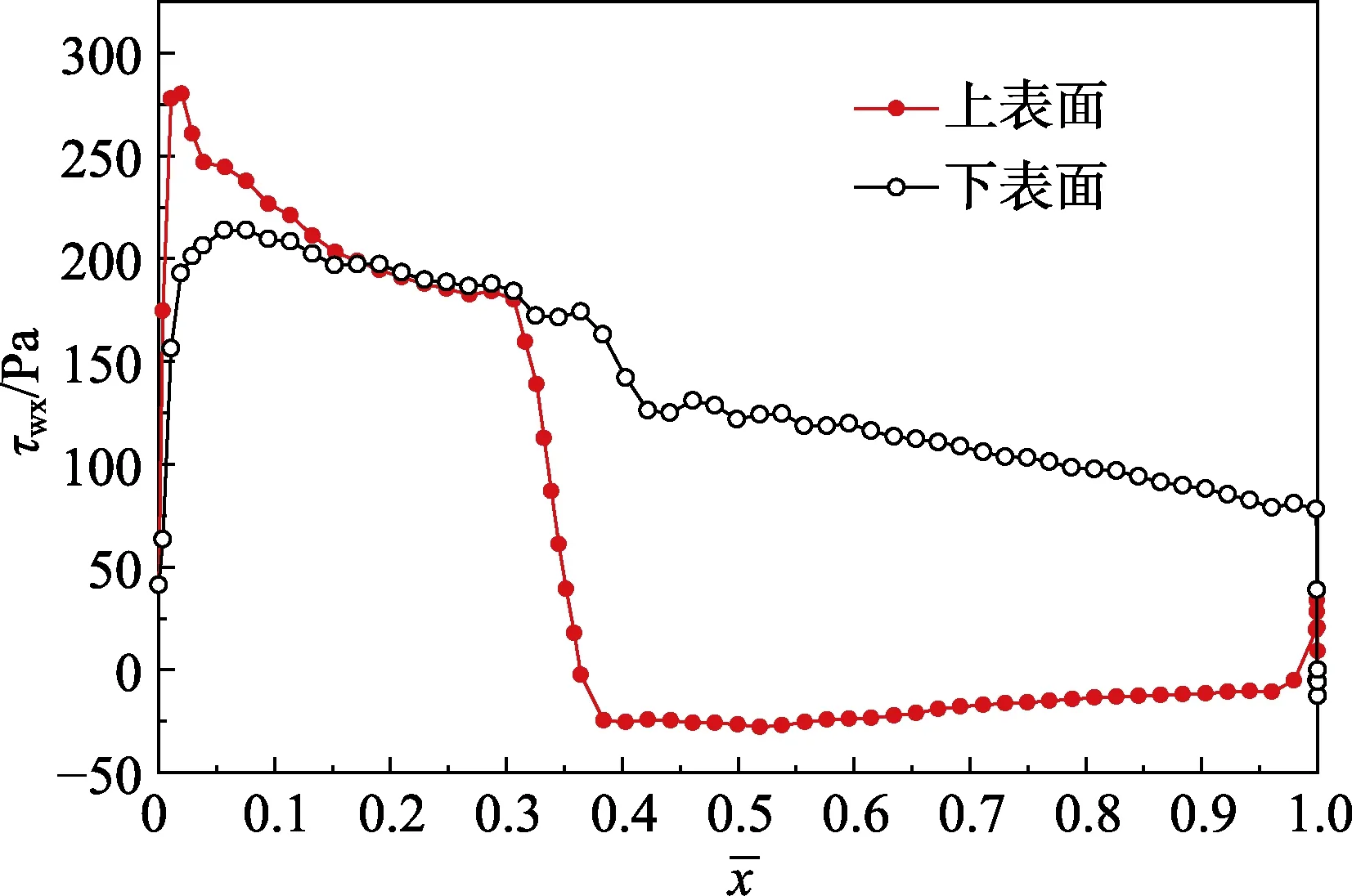
图6 对称面处翼型表面绕流切应力分布（来流马赫数0.8）

图7 是对称面处翼型时均流场密度等值线分布。可见，气流具有明显的可压缩性，翼型前缘气体密度最大，绕流通过局部激波压缩后当地密度迅速提高。

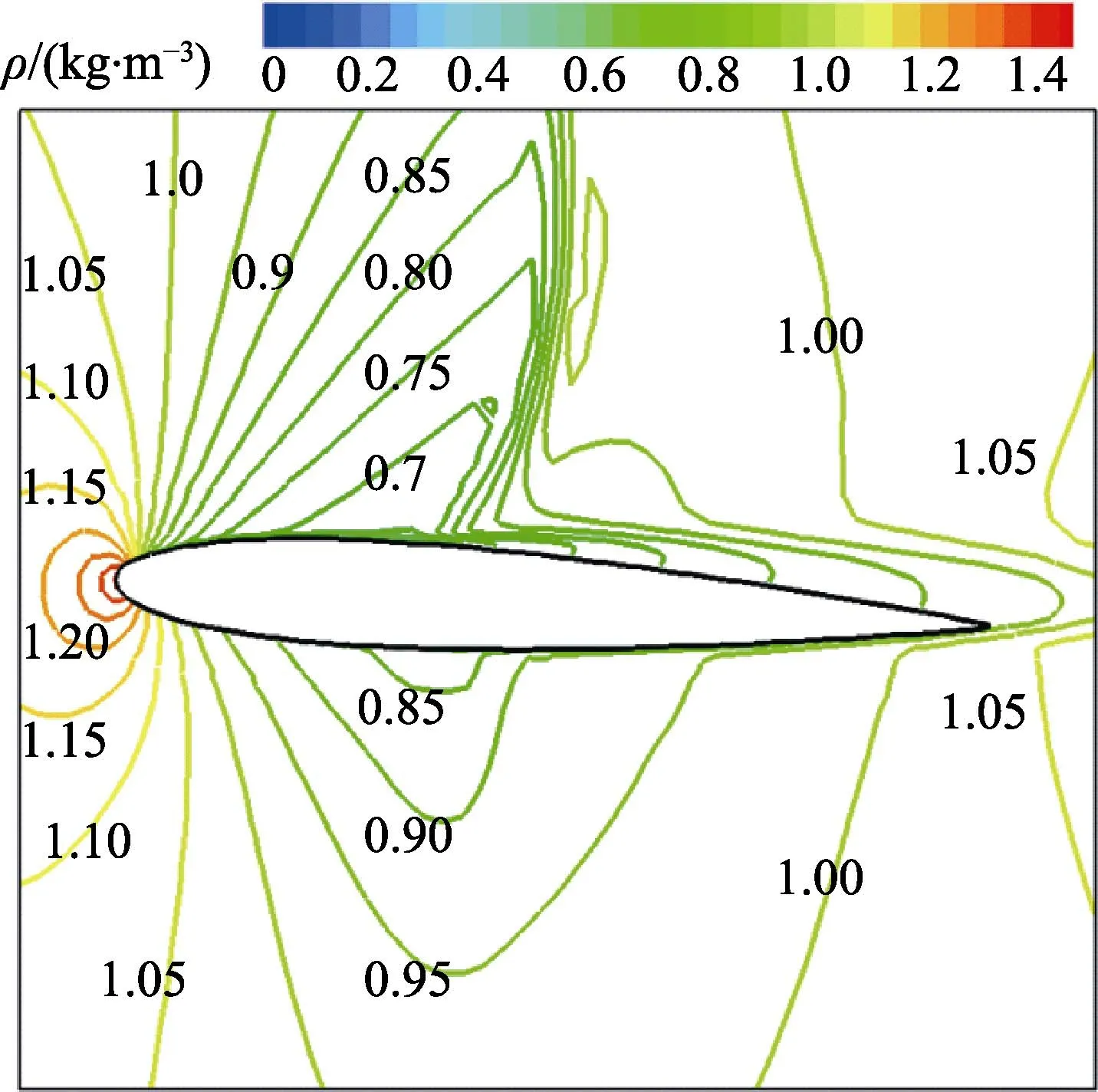
图7 对称面处翼型时均流场密度等值线分布（来流马赫数0.8）

4 结论

以FL-1 风洞NACA0012 翼型模型试验为研究对象，数值仿真亚跨音速试验的实际三维黏性流场，来流马赫数分别为0.5 和0.8，模型攻角为3.05°，获得以下主要结论：

（1）模型中部翼型表面绕流压强系数分布计算值与试验值符合良好，结构化网格和附面层网格构建质量高，湍流模型等选择合适，试验段上下透气孔板壁面所用模拟边界条件可行。

（2）来流马赫数对模型表面局部激波产生、位置和强度影响明显。基于风洞试验段来流总压和总温变化范围及出口气流静压试验参考值，在迭代计算过程对来流马赫数进行实时监视和调控，能够确保进口来流马赫数达到预定目标值。

（3）仿真结果清晰呈现了翼型表面附面层网格分布、可压缩流场流速和流线分布、局部激波及其诱导附面层分离等特性，有助于掌握模型整体气动力和局部细节流动机理。

（4）实际物理试验与计算机数值仿真之间相互配合，相得益彰，能够有效提升教学质量。