一种基于非支配排序遗传算法的社区发现算法
管文蔚,王艳兵
(徽商职业学院 电子信息系,安徽 合肥 230000)
在社区发现算法中,一般采用模块度来衡量社区划分结果的好坏程度[1]。模块度函数是由Newman和Girvan提出的一种用于评估社区划分的全局目标函数[2]。然而,由于受到模块度分辨率的限制,通常社区划分的结果是否最佳不能完全取决于模块化结果[3]。为解决此问题,文献[4]基于模块度密度的概念,克服了模块度分辨率极限问题。为了实现一次性得到不同分辨率下的社区发现结果,本文尝试优化模块度密度函数。扩展模块度密度是发现算法ratio association[5]与ratio cut[6]的凸组合,需要在不同参数设置下进行大量实验来克服分辨率限制问题。
对于扩展模块度密度,由于文献[4]中可调参数λ的加入,ratio association与ratio cut本身存在一定不足,各自分别趋向于发现大社区网络和小社区网络,这种特性很好地符合了多目标优化的定义。因此,这里将采用启发式算法中的一种基于非支配排序遗传算法尝试解决基于复杂网络中的社区发现问题,实现一次性得到多种不同分辨率的社区发现结果,以供决策者进行选择。因此,如何在减少计算量的情况下,尽可能多地得到不同分辨率下的社区发现结果是本文研究的重点。
1 多目标进化算法
优化问题通常可以按照目标函数的个数来分类:如单目标优化问题(Single-Objective Optimization Problem)和多目标优化问题(Multi-objective Optimization Problem)。不同于单目标优化问题中仅有一个评测目标,多目标优化问题中包含多个目标函数。本文应用多目标优化算法解决社区发现问题,多目标优化问题通常具有相互矛盾的目标函数,并且多目标优化问题通常情况下是一系列互不支配的解,而没有单一的全局最优解,称为帕累托(Pareto)解。这一点和单目标优化问题不同。
多目标优化问题可用公式(1)进行描述:
minimizeF(x)=(f1(x),…,fi(x),…,fk(x))
subjecttogi(x)≤0,i=1,2,…,p
hj(x)=0,j=p+1,p+2,…,m
(1)
其中,x=(x1,x2,…,xn)∈Ω是定义域在Ω上的n维决策变量,fi(x)是第i个目标函数。约束条件共有m个,其中不等式约束条件设为gi(x),共p个,等式约束条件设为hj(x),共m-p个。
当且仅当以下条件成立时,向量u= (u1,…,un),支配向量v= (v1,…,vn),upv:
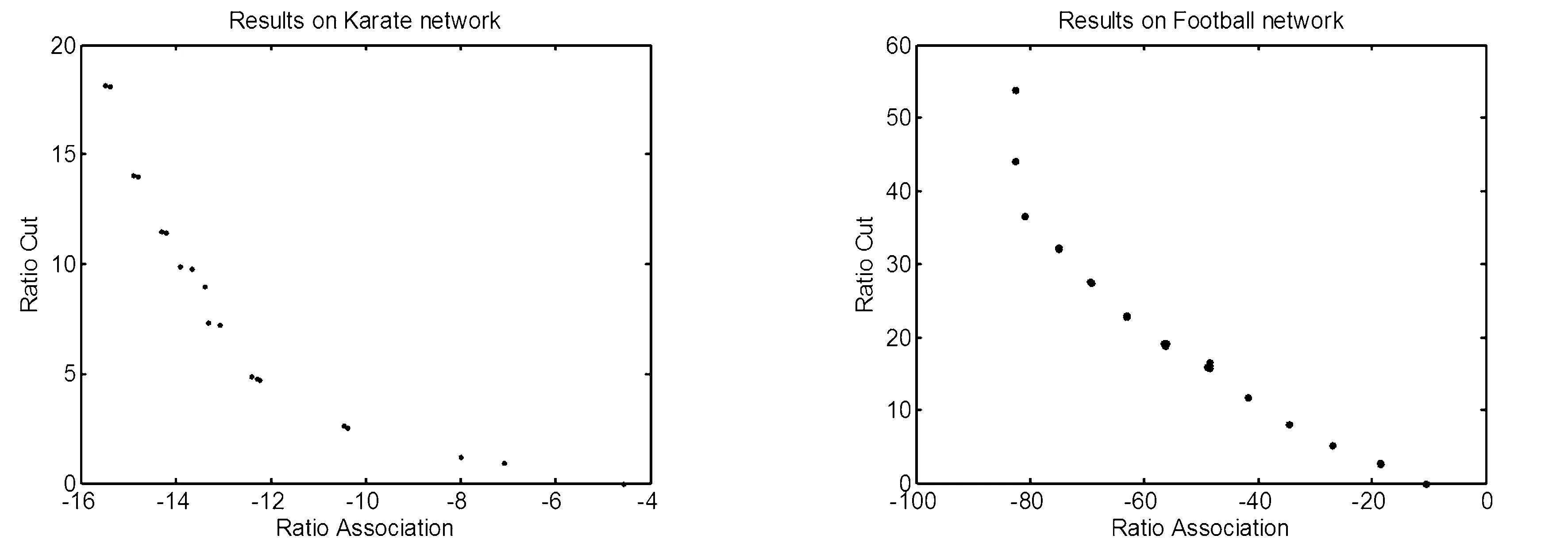
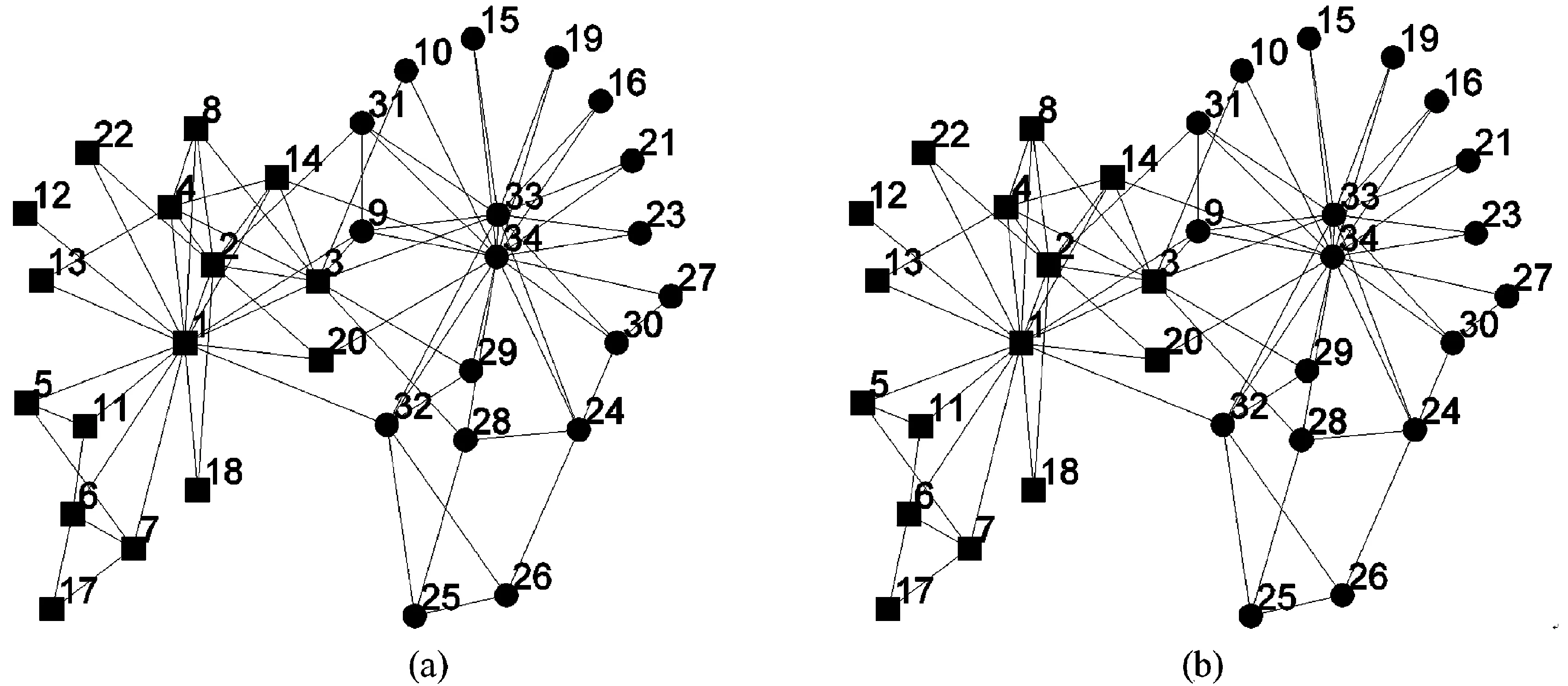
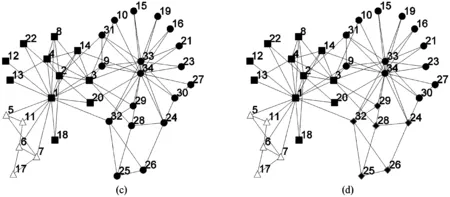
∀i∈{1,2,…,k}∶fi(u)≤fi(v)∧∃j∈{1,2,…,k}∶fj(u) (2) 对于给定的多目标优化问题F(x),Pareto最优解集P*定义为: P*={x∈Ω|∃x'∈Ω∶F(x')pF(x)} (3) 对于F(x)和Pareto最优解集P*[7],Pareto前沿(PF*)定义为: PF*={F(x)|x∈P*} (4) 在一个有|V|个节点和|E|条边的无向图G=(V,E),邻接矩阵为A。假定Vm和Vn为两个不相交的子集,模块度密度D定义为 (5) 之后,李珍萍等人扩展了模块度密度的定义,在原有基础上引入一个可调参数λ: (6) 式(6)中,当λ= 1时,其特例为ratio association;当λ= 0时,其特例为ratio cut;当λ=0.5时,等价于模块度密度D。优化ratio association的方法是将网络划分成若干小社区,而优化ratio cut的方法则是将网络划分成若干大社区[8]。对于扩展模块度密度,可通过调节参数λ的值,分析不同分辨率下的网络拓扑结构,克服分辨率限制问题。因此,我们可以简单地将这两个函数拆分开来,进行同时优化,就可以得到一组Pareto解,这样我们的两个目标函数可以设计为以下两个公式: (7) 由于训练样本本身没有图的结构,所以在初始化时首先建立一个最小生成树(MST),最小生成树能包含所有的节点且图中不存在回路。MST将相似度高的解连接在一起而相似度低的解则没有连接。当在图中移除两个节点之间的边时就会形成新的子图,一个含有K个社区划分的图需要移除K-1条边。在初始化过程中,每个个体首先移除一条边,当种群个体数超过边数时,接着随机移除第二条边,并以此类推。决定一条边是否移除时主要考虑节点之间边的权重,权重越大,移除的可能性就越大。这样能保证得到一组相对高质量的初始解。 在交叉这一步中,采用均匀交叉算子来产生新的个体,这种交叉方式对父代没有偏好且能够继承父代的结构特点但又与父代结构不同。首先,随机产生一个长度为N取值范围为{0,1}的标志mask来决定子代的基因型取决于哪个父代。当mask(i)为0时,子代的第i位基因型继承父代a,否则继承b。 当随机更改节点之间的连接时会导致算法效率不高,因为对于一个大小为N的数据集,随机更改节点之间的连接时的搜索空间为NN,所以我们有必要有目的性地更改这些连接。在本文中,这里采用近邻偏好变异方式来减小搜索空间。在近邻偏好变异机制中,个体的第i个基因位gi根据节点i与其他节点之间的连接的权重大小排序来进行变异,而且变异后只允许与L-近邻(L< (8) 在一个大小为N的数据集中,对于两个节点i和j,它们分别与各自的l1-近邻和l2-近邻相连,且l1>l2,特别是当与j相连的节点属于它的L-近邻之一时,那么节点i相对更容易变异。在近邻偏好的变异策略中,一个与其l-近邻相连的节点的变异概率定义为公式(8)。这样,节点i就能获得比节点j更高的变异率。 基于NSGA-Ⅱ的社区算法描述见表1。 表1 基于NSGA-Ⅱ的社区发现算法流程 本文所提算法需要设置的参数如表2所示: 表2 基于NSGA-Ⅱ的社区发现算法参数设置 这里将基于非支配排序遗传算法的社区发现方法用于社会学家Zachary的空手道俱乐部社会关系数据集(称为karate数据集)和USA大学生足球联赛俱乐部社交网络数据集(称为football数据集),接着利用标准互信息指标(简称NMI)进行测试,并展示了社区关系网络发现结果。 图1 真实社区结构1(Zachary空手道俱乐部成员网络) 空手道俱乐部网络是由社会学家Zachary用了两年时间在大学空手道俱乐部中观察34名俱乐部成员之间的社会关系网络[9-10]。最后,一个社区变成了两个社区,如图1所示。这主要是因为空手道教练辞职后有部分队员与教练一同离开,形成了新的社交关系网络。 USA大学生足球联赛俱乐部社交网络数据集是Newman和Girvan两人观察的2000年秋 季USA大学生足球联赛常规赛季 的比赛网络数据[11-12],根据赛区划分将球队分成115个节点,因此,网络中每个节点表示一个球队,两个节点之 间进行的比赛由 网络中的连接线表示。每个节点在常规赛季中平均要有11条连接线,包括7条赛区 内的连接和4条赛区间的连接。该社交网络数据集中共有115个球队和616场比赛,所有的球队被划分成12个赛区,也就是12个社区。 首先,我们将对基于NSGA-II的社区发现算法所得PF (Pareto Frontier)图进行分析,如图2。由图中可以看出,算法在两组测试网络上都能得到一组非支配解,每一个非支配解都对应了一个Dλ混合参数。值得说明的是,并不是所有的解都对应不同的混合参数,在PF图中互为近邻的解可能对应相同的混合参数。如此一来,一组PF解救对应了不同分辨率下的社区划分。由于在多目标算法中,优化ratio association的算法和优化ratio cut的算法被同时考虑。因此,所得结果为优化这组函数的折中解,决策者可以根据自身需要,选择不同分辨率下的社区划分结果。 (a)算法在karate网络所得PF (b)算法在football网络所得PF 为了进一步证明本算法的有效性,这里随机选取算法在karate网络上所得解并给出其对应的社区划分情况,如图3。图3(a)与(b)得到了与真实划分一致的解,(c)中所得划分得到了三个社区,其中将原有的一个大社区分为了两个,(d)所得划分与(c)类似,同样是将大的社区划分为两个小社区。如此一来,我们可以根据决策者的需要选取合适的划分,这也是采用多目标算法进行优化社区发现的最主要的优点。 图3 随机选取Karate网络PF中的解对应的社区划分情况 本文提出了一种基于非支配排序遗传算法的社区发现方法。在复杂网络中,一个社区内不同节点间的连接比较紧密,而不同社区之间节点间的连接相对来说更加稀疏。所以,可以采取两个不同文中所采用的目标函数的物理意义。基于这点考虑,就从多目标优化的角度来解决复杂网络社区发现问题。本算法主要优势如下:(1)采用多目标实现社区发现;(2)社区数目自适应;(3)决策者根据自身需要选取合适的社区数目,无需固定。并且实验证明了采用基于NSGA-II算法进行社区发现的有效性。2 基于NSGA-II的多目标社区发现
2.1 目标函数
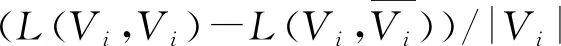
2.2 初始化
2.3 交叉
2.4 变异
2.5 算法描述

3 实验结果及分析
3.1 参数设置

3.2 现实网络举例

4 结语

