贸易信用交易下的保险投资策略研究

刘 露， 邓伟升， 董兴林， 李雅婷

（1.山东科技大学 经济管理学院，山东 青岛266590；2.云南大学 工商管理与旅游管理学院，云南 昆明650091；3.南开大学商学院，天津300071）

0 引言

融资难是长期困扰中小企业的难题，为保障供应链运作效率，为中小企业提供贸易信用融资成为各行业共识，2017年我国仅规模以上工业企业应收账款额就高达13.5万亿元。然而，融资风险成为困扰核心企业新的难题，据保险巨头Coface调查显示，2017年我国超过68%的企业存在商业信用逾期付款现象，这同时也是引发供应链资金流断裂，造成企业破产的关键因素。为了应对中小企业违约风险，核心企业开始自发购买贸易信用保险，以应对这类不确定性。本文期待解决以下关键问题：贸易信用保险下企业如何制定最优运营决策？企业应当在何时投资和购买商业保险？

近年来，学者针对贸易信用融资在供应链运营中的关键作用展开了诸多研究。其中，Gupta等［1］较早从运营层面对这类模式开展研究，分析信用期等贸易信用融资参数制定对企业最优化库存决策等的影响和变化。Luo等［2］则进一步将延期支付融资研究拓展至信息不对称情形，发现非对称信息下虽能提升买方收益，但无法实现链内协调。陈祥锋［3］论证延期支付融资形式在供应链协调中的作用，发现延期支付有利于激励零售商订货，并起到供应链部分协调作用。与之类似的还有Lee［4］和Chen等［5］的研究。此外，还有学者设计实现延期支付供应链协调新的契约机制，如王志宏等［6］设计实现零售商信息披露的商业信用激励契约机制。Zhang等［7］设计实现延期支付供应链协调的数量折扣合同。李荣等［8］分析供应链上下游企业均存在风险偏好情况下的延期支付类供应链协调问题。除此之外，冯海荣等［9］和Chen等［10］则分别对易腐品联合采购费用分配问题及库存和信用期联合决策问题进行研究。王文利等［11］将延期支付研究框架拓展到两周期环境，并与传统供应链进行比较，分析交易信用和零售商初始资金对订货决策影响。Cao等［12］对贸易信用交易背景下低碳供应链运营协调开展了研究。Kouvelis等［13］比较贸易信用融资和银行融资，论证了贸易信用融资的运营优势。虽然贸易信用融资和运营结合管理领域积累了诸多研究，但上述研究并未讨论贸易信用融资保险的运营策略。

保险作为一项有效的风险管理工具，同样成为学术研究的焦点。Li等［14］针对应收账款融资中的保险策略给予研究，发现投保有助于提升供应链运作效率。Jin等［15］进一步针对银行融资情境下的最优库存和保险联合决策问题展开了研究。于辉等［16］将营业中断保险应用于供应链风险管理，发现投保有助于实现供应商、零售商及保险公司三方共赢。杨雷等［17］探究退货运费险对供应链运营的影响，发现运费险存在“市场失灵”的情况。陈静等［18］制定应对农副产品产出不确定风险的商业保险运营策略。王文利等［19］发现交易信用保险有助于激励供应商为零售商提供融资，为供应链创造价值。

与本文类似的研究是文献［19］，但该研究未讨论零售商初始资金这一关键参数对企业融资保险运营投资策略制定的影响；此外，研究讨论的是一个相对简单的单层优化决策问题。本文期望基于Stackelberg博弈方法，通过建立双层规划优化博弈模型，一方面探究贸易信用融资下供应链运营和保险的联合最优决策；另一方面，借助CVaR等风险度量方法，探究生产商风险厌恶、零售商初始资金量等关键运营和融资参数对保险策略制定的影响。以期为贸易信用保险的合理实施提供行之有效且科学的运营策略指导。

1 模型构建

考虑由单生产商及单零售商组成的两级分销系统，零售商R从生产商M处以批发价w（生产商决策变量）采购q（零售商决策变量）单位商品，该产品单位生产成本为c。零售商以售价p销售商品，并以剩余价值s处理过剩商品。各类价格间满足p＞w＞c＞s，即生产商和零售商都可以通过销售新产品获利，但销售剩余产品无利可图。市场需求Z具有随机性，通过市场调查研究可获知其服从［0，+∞］间分布及密度函数分别为F（x）和f（x）的概率分布。令F（x）＝1-F（x），并假设该概率分布同时满足递增失效率和广义递增失效率［20］，即满足递增的性质。

执行交易时零售商所具备初始资金量为η。显然，当η≥wq时，零售商并不缺乏订货资金（资金充足）；而当η＜wq时，零售商资金缺乏，生产商可以为其提供贸易信用融资（订货时不足的货款通过期末销售收益偿还），零售商所需融资额度为wq-η。此时，资金约束的零售商可以选择参与融资或不参与，而处于供应链上游的生产商可以选择为其提供贸易信用融资或者不提供，一旦融资发生，生产商为零售商赊销wq-η的信用额度，而零售商需要用销售回款pmin｛Z，q｝+s（q-Z）+予以偿还欠款。这意味着当市场需求低于一定程度时，零售商销售回款较少，此时不足以覆盖贸易信贷额度，即pZ+s（q-Z）+＜wq-η。这时当需求临界点θ满足Z＜θ（q，w）时，零售商全部销售收益被予以偿还欠款，零售商被执行破产清算（假设零售商不存在多余资产，这符合现实背景）。这意味着零售商破产需求临界值为θ（q，w）。生产商在为零售商提供贸易信贷合同时，同样面临和承受着零售商因销售不力造成的违约风险，此时生产商可以选择为交易投资保险策略，假设其投保额度为wq-η，生产商须为该交易支付保费，经核算后保险费率为r（保险公司决策变量），生产商支付贸易保险成本总额为（wq-η）r。同时，保险公司I处于完全竞争市场，仅获取无风险保险费率。

与大多数供应链相关研究文献一致，本文采用Stackelberg博弈刻画生产商及零售商间的博弈关系，并分析其均衡博弈策略。生产商为博弈领导者，双方首先明确融资策略及投保策略（是否融资、是否投保），随后决策令自身收益最大化的批发价、订货量等最优决策。用上标T，K，N，A分别表示贸易信用且不投保、贸易信用投保、资金约束但不融资、资金充足四类情形；上标*和0表示供应链分散式及集中式决策情形下均衡策略（分散式决策是指各决策主体分别以自身利益最大化为目标进行决策；而集中式决策则指决策者以供应链整体利益最大化为目标进行决策）；i＝M，R表示供应链成员，j＝T，K，N，A表示各资金情形，Πji表示j情形下决策者i期望收益（效用）大小，令k＝p-s，t（w）＝w-s，分别表示因产品未能售出造成的零售商单位产品潜在利益损失和生产商单位产品潜在利益损失。需要特别说明的是，以上模型参数假设中，除保险费率r，批发价w，订货量q为决策变量外，其余均为外生参数，这符合经典“报童”模型及大多数相关文献［2～8］的基本假设。下面依次分析供应链在各资金情形下的最优运营决策，并对关键参数的影响予以分析。需要特别说明的是，为保障正文内容更加简洁和连贯，文中所有命题及推论证明过程均以附录形式呈现。

2 贸易信用融资

与大部分文献［3～8］类似，本文专注于分析贸易信用对企业运营层面的影响，而不再单独考虑贸易信用为供应链所创造的额外成本和价值。因此，依据模型构建部分假设及市场需求实现值，列出生产商及零售商收益表达式如下：

经计算可知生产商及零售商期望收益值分别为：

鉴于融资过程中，生产商需承担风险，考虑其风险态度的影响尤为关键。在选取风险度量准则时，总结发现，相比均值方差、VaR等方法，CVaR准则具有反映超额损失、适用非正态分布、等价于凸规划等优势［20］。本文选取CVaR准则来刻画生产商风险下的效用函数，以探究其风险态度对最优决策制定的影响。给出CVaR准则相关定义如下：

定义1令αM∈［0，1］表示决策者风险偏好因子，表示分位数，

表示满足置信水平为αM的分位数。此时贸易信用融资下生产商关于批发价wT的条件风险值（CVaR）可被重新定义为：

对表达式（5）进行进一步推导分析可得到该式等价形式。令（wT）＝-（w T，Z）］+，经推导后可知，决策者条件风险效用值被简化为：

显然有z2＞z1成立。首先分析求解最优分位数可知，有如下结论成立：

命题1存在最优分位数＝z2，使 得CVaR（）＝（wT，）。

由命题1证明可知，风险厌恶型生产商期望效用函数可被刻画为：

以上给出了贸易信用融资下的供应链成员期望效用表达式。基于此，下面进一步对成员博弈下的均衡决策情况予以分析。参见文献［21，22］，根据Stackelberg博弈的逆序求解算法思路，批发—订货型供应链中，生产商（主导者）和零售商（跟从者）主从博弈的均衡策略求解过程可被转换为如下双层规划优化模型［21，22］：

即：在给定其他外生参数的基础上，作为博弈领导者，生产商首先决策最优批发价wT*，但生产商在决策前需首先预估零售商关于其批发价决策的最优反应，以做出最优批发价决策的应对策略。因此，问题（8）模型求解算法第一步为，在假设wT为给定参数基础上，根据零售商决策目标（qT，w T），求解零售商最优订货量关于批发价最优反应函数qT*（wT）；第二步，将qT*（wT）代入生产商决策目标函数（wT，qT*（wT））中。此时，问题（8）转变为一个一元函数单层规划最大化求解问题，通过最优化求解即可获得生产商最优批发价wT*；随后，将w T*代回qT*（wT）以获得均衡状态下最优订货量qT*；最后，将wT*，qT*代入（wT，qT），（wT，qT）中，以获得均衡状态下生产商、零售商最优期望效用值。

下面，在给定wT的情况下，首先求解零售商最优订货量关于批发价的最优反应函数qT*（w T）可知，有如下命题2结论成立：

命题2给定wT，分散式贸易信用供应链零售商最优订货决策qT*（wT）满足

由命题2，经简单推导可知，有如下推论1结论成立：

推论1（1）给定wT，qT*（wT）随着η的增加而减少；（2）qT*（wT）随着w T的增加而减少。

命题2给出了零售商订货量关于批发价的最优反应函数qT*（wT），下面进一步求解生产商的最优批发价决策w T*，有如下命题3结论成立：

命题3当H（x）为凸增函数［23］，为关于w T的单峰函数，且最优批发价决策w T*满足

命题3给出了均衡状态下的最优批发价决策w T*，进一步将w T*代入（9）式qT*（wT）中即可获得均衡状态下的最优订货量决策qT*。进而可获得决策者最优期望收益和。

3 投保策略

意识到需承担零售商违约风险，生产商可选择为交易购置保险。生产商支付保险费率r K以为贸易信用额度wKqK-η投保，并与保险公司共同监控零售商销售。一旦零售商出现违约，保险公司将零售商违约部分赔付生产商（最高赔付额度w KqK-η），确保生产商不因违约而受损。

显然，在执行投保策略后，零售商的收益函数表达式不变，仍然与传统的贸易信用融资中表达式一致。而由于生产商投入保险，其无需承担零售商的违约风险，因此生产商在投保策略下的期望收益函数变为：

而作为保险公司，需要承担零售商违约风险，经核算，其期望收益表达式为：

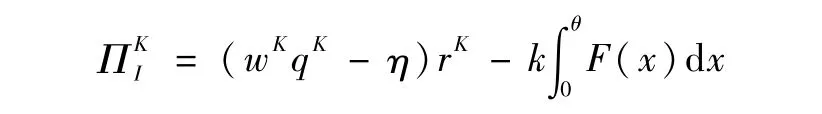
下面分析保险策略下均衡决策情况。这是一个三层规划问题，保险公司首先决策保险利率r K*。随后，生产商决策批发价wK*。最后，零售商决策订货量qK*。由于零售商的期望利润函数与形式上是一致的，显然，零售商订货最优决策形式qK*（w K）也与第2节中命题2是一致的，即qK*（w K）满足

下面分析生产商的最优批发价决策w K*（r K）。传统的求解思路是，将qK*（wK）代入中，并求解，qK*（wK），r K）。根据文献［21］，该问题等价于：给定wK*（qK）满足

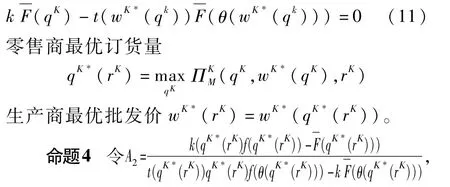
给定r K，当H（x）为凸函数时，保险策略下零售商最优订货量决策qK*（r K）满足

在已知qK*（r K）和wK*（r K）后，下面分析保险 公司的最优保险利率决策。由于保险公司处于竞争型资本市场中，其仅能获得市场的无风险保险收益率，因此，保险公司的最优保险利率决策应满足下述命题：

命题5贸易信用保险下，保险公司最优保险利率r K*满足

4 无融资情形

进一步探讨当零售商不进行融资时的供应链均衡运营决策情况。由于不存在贸易信用融资，零售商期望收益函数表达式与传统报童模型类似。风险中性零售商与生产商期望效用表达式可被分别表示为：

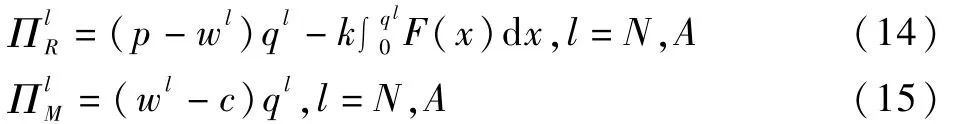
下面对两种资金情形（情形A和情形N）下供应链均衡决策进行分析。

A资金情形下，生产商及零售商均能够取到期望收益极值对应的最优决策。类似第3节分析可知，博弈均衡策略存在且唯一。同样运用逆序求解法依次求解一阶条件（qA）关于qA的方程式，以及（wA，qA*（w A））关于wA的一阶条件表达式，即可得到均衡最优状态下的供应链成员决策满足下式：

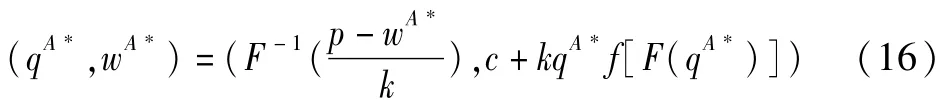
N资金情形下，零售商面临资金缺乏，但未借助贸易信用进行融资，此时零售商仅通过使用自有资金η完成订货，其订货量始终为：

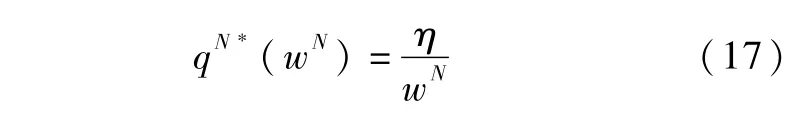
将零售商订货反应决策代入生产商期望效用函数表达式后可知

5 参数灵敏度分析

以上分析了各资金情形下供应链企业博弈的最优均衡运营决策。下面进一步分析融资中的关键参数，如零售商初始资金、生产商风险厌恶程度等对供应链融资及保险运营的影响。

首先分析零售商初始资金对均衡资金模式的影响。令La＝wa*qa*＝min｛wT*qT*，wK*qK*｝，Lb＝wb*qb*＝max｛wT*qT*，w K*qK*｝，Lc＝wA*qA*，分析各资金情形发生的具体条件，可知：

命题6（1）当η＜min｛La，Lb，Lc｝时，资金情形及发生条件可总结为：

（2）当η≥Lc时，零售商资金充足，情形A发生；

（3）当η＜Lc时，且当La≥Lc时，零售商在η∈［0，Lc］区间的资金情形如命题6（1）所示；当Lb≥Lc≥La时，零售商在η∈［0，La］区间的资金情形如命题6（1）所示，在η∈［La，Lc］区间，当≥和同时满足时，b情形发生，否则N情形发生；当Lb＜Lc时，零售商在η∈［0，La］区间的资金情形如命题6（1）所示，在η∈［La，Lb］区间，当和同时满足，b情形发生，否则N情形发生，在η∈［Lb，Lc］区间，N情形发生。

对命题6的解释如下：显然，当η≥Lc时，零售商资金充足，无需融资，此时情形A发生；当η＜Lc时，根据La，Lb，Lc的大小关系，又可分为三种情况：La≥Lc，Lb≥Lc≥La，Lb＜Lc。鉴于相似性，仅讨论Lb＜Lc时的情况，此时，当η∈［0，La］时，资金发生情形及条件如命题6（1）所示。对于生产商而言，其可以为零售商提供融资模式T和K，也可以选择不为零售商提供融资（迫使零售商选择N）。而对于零售商而言，其可以选择接受T或K，也可以主动选择N。这主要取决于双方在各情形下的收益，以及资金情形选择博弈均衡情况。当η＜min｛La，Lb，Lc｝时，零售商相比T，K，A三种资金情形均是资金约束的。即T，K融资情形均有可能发生。此时当≥max｛｝，≥时，生产商和零售商均选择T融资情形，此时的博弈均衡策略显然为T模式；当满足条件≥，≥时，生产商的最优策略是选择K情形，但对于零售商而言，其宁可选择N情形，生产商不得不选择折中策略—为零售商提供T模式，（1.2）（1.3）的分析是类似的；当η∈［La，Lb］时，零售商在a情形下不再资金约束，仅有b情形和N情形可能发生，只有当生产商和零售商均选择b情形时，b情形才会发生；当η∈［Lb，Lc］时，零售商自有资金相比T，K情形下所需订货资金均是资金充足的，即零售商虽然相比A情形资金约束，但却无法获得T，K融资，此时N情形发生。

以上分析了零售商资金量对融资模式均衡的影响。下面进一步针对相关关键参数，如零售商资金量，生产商风险厌恶程度等对供应链运营的影响作出分析。此前，给出集中式供应链的最优决策。情形K，情形A，情形N情况下，由于决策者均为风险中性，集中式供应链效益函数可直接定义为：

而T情形下，由于包含风险厌恶型生产商，参考文献［24］定义，将含有风险厌恶型决策者的集中式供应链决策目标定义为帕累托最优函数。令αR表示零售商风险偏好因子（本文中αR＝1），情形T下的集中式供应链决策目标可被定义为：

通过对参数η，rF，αM等的灵敏度分析可得到如下结论：

命题7（1） 随着αM的增加，增加；

以上分析表明：（1）融资及保险对于供应链具有正向激励作用。可以发现，当零售商资金量足够低时，K情形下的零售商订货量反而升高至集中式供应链水平，同时，供应链整体收益也提升至集中式水平。由推论1，固定wK，rK，零售商订货量随着其初始资金量的降低而增高。这是由于对于零售商而言，融资相当于生产商为其分担了部分风险。其资金量越低，破产风险越大，生产商为其分担的风险也越高，这反而激励着零售商增加订货。但当wK，rK不是固定值时，由于零售商将风险传递给保险公司，保险公司通过提升保费来覆盖风险，生产商不得不为保费的提升“买单”，这增加了生产商运作成本，此时作为博弈主导者，生产商会选择提升批发价来弥补这一成本损失，这间接增加了零售商订货成本。但随着零售商资金量的降低，意识到生产商必然会提升批发价，零售商只能通过提高订货量来尽可能多的获取上游企业风险分担带来的“收益”，以弥补批发价提升带来的损失。最终，批发价和订货量的提升使生产商和保险公司获益，而使得零售商受损。当η和rF降低至0时，生产商收益达到集中式供应链收益水平，但零售商收益降低至0。可见，融资及保险能够为供应链和生产商创造价值，但过分依赖融资对零售商是不利的。而作为供应链核心企业，生产商可以通过补贴的形式鼓励零售商放弃使用自有资金，而更多的参与到融资当中，以实现双方共赢。

（2）对于生产商而言，是否投保应取决于其自身的风险厌恶程度，以及保险市场的无风险利率水平。命题7表明，当η→0且αM＞0时，投资保险（情形K）能够使得供应链收益达到集中式收益状态，而不投保（情形T）则无法达到集中式收益水平。这是由于，贸易信用融资中，供应链的主要风险是零售商的破产违约风险，而这一风险通常是由零售商过量订货造成的。因此，风险厌恶的生产商通常会选择提高批发价来遏制零售商的过量订货行为。但这也引发生产商自身订货收益的降低，进而引发其期望效用水平的下降。而投保有助于实现风险转移，从而消除生产商风险厌恶造成的不利影响。可见，对于风险厌恶的生产商而言，投保不仅意味着风险的降低，同时意味着其收益的提升，有助于实现风险和收益的共赢。但值得注意的是，当保险市场的竞争程度并不高，保费市场的无风险利率水平较高时，高额的保险费率对生产商不利。可见，影响生产商是否投保的关键因素是其自身的风险厌恶水平，以及保费市场的竞争程度。当生产商风险厌恶水平较高、保险市场竞争程度较高时，投资贸易信用保险能够为生产商和供应链创造价值，否则，生产商应当放弃投保。

6 数值分析

为更加直观理解结论内容，并对相关结论予以补充延伸，下面借助数值分析工具进一步补充分析论证相关理论结果。参数随机获得并设置如下：p＝8，c＝3，s＝2，Z～N（50，20），αM＝0.8，η＝10，数值仿真结果见图1至图3。可以发现：

（1）随着零售商初始资金量的增加，均衡状态下的资金模式依次变为K、T、N、A四种模式。这是由于，当η∈［0，η1］时，有＞＞，即双方均选择K模式；当η∈［η1，η2］时，Π＞，均衡融资模式变为T模式；当η∈［η2，η3］，＞，生产商不会为资金约束的零售商提供融资，均衡资金模式为情形N；当η∈［η3，+∞］，零售商资金充足，无需融资，均衡资金模式为情形A。

（2）融资为供应链创造收益，并同时实现生产商和零售商共赢。由图1和图3可知，相比情形A和情形N，当零售商资金量较低（即融资开展深入程度较高时），情形T和K下生产商及供应链收益更高。同时，随着零售商资金量的下降，融资深入程度提高，生产商和供应链收益增长越快。可见，融资为生产商和供应链创造直接价值。对于资金约束零售商而言，由可知，融资同时对其有利。可见，融资的开展有助于实现供应链成员共赢。但值得注意的是，随着η的下降，零售商收益降低，即，过分依赖融资对零售商不利，资金约束的零售商在参与融资时会尽可能多的提供自有资金，这反而对生产商不利。对于生产商而言，其可以通过补贴的形式鼓励零售商放弃使用自有资金，而更多的参与融资。

图1 零售商初始资金对生产商效益影响

图2 零售商初始资金对零售商效益影响

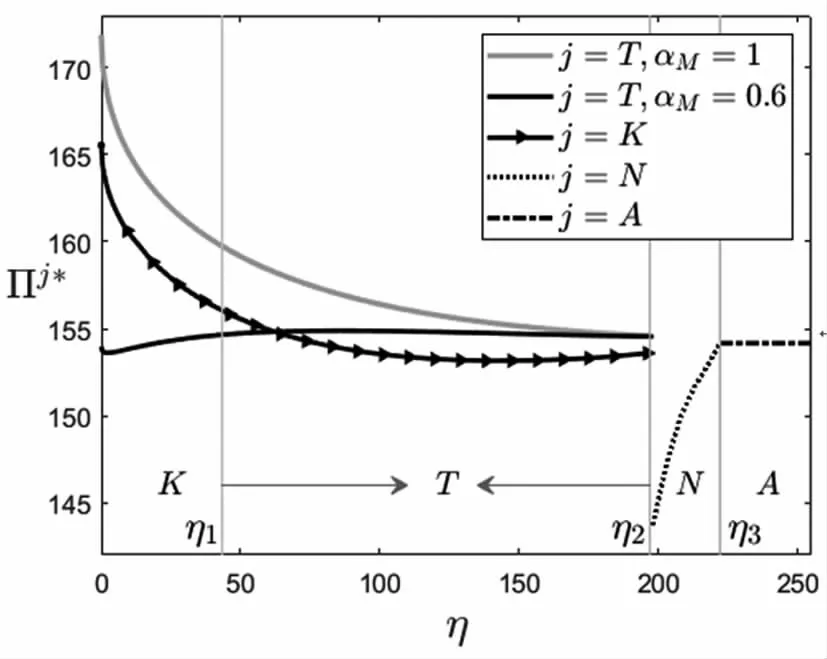
图3 零售商初始资金对供应链效益影响

（3）当αM＝1时，生产商的风险厌恶程度较低，生产商所制定的运营决策受风险厌恶影响程度较低。而投保意味着必须付出一定的保费成本。风险追求的生产商更倾向于享受高风险、高收益（）。随着生产商风险厌恶程度的提升（αM下降），生产商和零售商期望效用同时下降，这源于风险厌恶的生产商所制定的保守批发价决策。此时，由于无需承担风险，保险策略（模式K）展现出优越性。可以发现，当α＝0.6，且η∈［0，η1］时，，即投保既可以帮助生产商转移风险，同时有助于提升其收益。但随着η的上升，保险策略逐渐丧失优势，这是由于的上升意味着风险的下降，生产商风险厌恶带来的影响逐渐下降，这时生产商应放弃投保。

可见，生产商是否选择投保，应取决于其风险厌恶程度、零售商初始资金量、保险市场竞争程度等因素。当生产商风险厌恶程度较高、零售商初始资金量较低、保险市场竞争程度较高时，贸易信用保险能够为生产商及供应链创造价值；否则生产商应当放弃投保。上述结论同时符合命题6和7的预期。

（4）生产商的投保策略同时为零售商和供应链创造价值。由图2和图3不难发现，当αM＝0.6且η＜η1时，有，ΠK*＞ΠT*成立，这意味着，当生产商风险厌恶程度较高且零售商资金量较低时，生产商投保能够实现生产商、零售商以及供应链整体的共赢。并且，由图3可知，生产商风险厌恶程度越高、零售商资金量水平越低，保险为供应链创造的价值越显著（ΠK*-ΠT*随着αM，η的降低而增加）。

传统研究发现，当零售商资金量趋于0时，贸易信用机制能够实现供应链协调（使分散式供应链收益达到集中式供应链水平）［4，5］，而结合命题7及图3发现，生产商的风险厌恶造成贸易信用供应链失调（当η→0时，ΠT*远低于ΠT0）。而保险投资有助于实现供应链的再协调（当η→0且r F→0时，ΠK*→ΠK0＝ΠT0），这再次体现了贸易信用保险投资的价值。

7 结论

贸易信用是解决中小企业融资难题的主要途径，而贸易信用保险正成为解决融资风险的重要手段，本文对贸易信用融资保险的优化运营策略予以研究。用CVaR准则刻画生产商效用函数，并通过Stackelberg博弈模型刻画融资模型，分别建立并分析了贸易信用、贸易信用保险、资金约束无融资、资金充足四类资金模型，给出了最优运营决策，并分析了零售商资金量、生产商风险厌恶程度等关键参数的影响。主要发现：（1）零售商初始资金量是影响供应链运营决策、融资模式选择均衡的关键因素，应合理布局使用；（2）贸易信用融资的实施有助于实现生产商及零售商间的共赢，但随着融资开展的不断深入，生产商既得利益逐步增加，零售商期望利益则逐渐下降，生产商可通过补贴的形式化解矛盾；（3）生产商应合理投保，当其风险厌恶程度较高、零售商初始资金较低、保险市场竞争程度较高时，保险能实现生产商、零售商及供应链共赢，应选择购买保险；否则应当放弃参保；（4）贸易信用保险能够为供应链创造价值。当生产商风险厌恶程度较高，传统贸易信用机制无法实现供应链协调，而保险投资有助于实现贸易信用供应链再协调。

本研究对于贸易信用融资保险的实施提供了行之有效且科学的运营决策和实施方案，对于供应链开展运营和财务结合管理具有积极的推动意义。但文章是建立在零售商完全守信，信息完全对称，供应链结构相对简单的假设下进行的，未来可拓展相关研究。也可以针对其他类型的融资风险，讨论融资保险的价值。