基于三角模糊化的Mamdani模糊系统输出算法

陈 雪, 王贵君

(天津师范大学 数学科学学院, 天津 300387)

模糊系统的本质就是输入和输出之间的映射关系, 具有可同时处理数据信息与语言信息的特点, 其中语言信息处理通过一组IF…THEN规则完成, 而数据信息是对系统参数进行合理调节的外部条件. 模糊系统与其他系统的主要区别在于一般系统通常通过微分方程或代数方程描述, 具有确定的数学模型, 而模糊系统主要基于语言规则描述, 并通过模糊推理实现. 目前, 以Mamdani和Takagi-Sugeno (T-S)为代表的两类模糊系统研究已取得了很多研究成果. 例如： Wang等[1]采用正则最小二乘法和基函数研究了Mamdani模糊系统的逼近性, 并应用Stone-Weierstrass定理证明了该模糊系统对连续函数的逼近性; 刘普寅等[2-3]基于分片线性函数研究了广义Mamdani模糊系统对一类可积函数类的泛逼近性; 文献[4-5]讨论了两类特定Mamdani模糊系统的通用(泛)逼近性; 唐少先等[6]借助前件模糊集给出了单输入、 单输出SISO-Mamdani模糊系统的解析表示和隶属函数优化方法； 孙富春等[7]给出了SISO-Mamdani模糊系统构成函数逼近器的必要条件. 上述研究结果为拓广模糊系统的建模和逼近性奠定了理论基础. 文献[8]通过引入拟减算子定义了K-积分模, 并以此积分模为度量研究了Mamdani模糊系统对一类可积函数的逼近性; 文献[9]基于网格剖分和矩阵模概念构造了非齐次线性T-S模糊系统, 并在最大模意义下证明了该模糊系统对连续函数类构成逼近器[10-11]; 高建思等[12]通过引入高斯模糊化求解出前件为三角模糊数时后件输出模糊集的隶属函数, 并给出了三角模糊化和高斯模糊化的两种Mamdani模糊系统的表示. 这些结果主要是对不同类型的Mamdani模糊系统给出具体的解析式, 并未对计算输出值问题进行研究.

周洁等[11]以Bernstein多项式为规则后件建立了多输入、 单输出模糊系统, 并首次通过随机剖分数所确定的Bernstein多项式给出一类模糊系统的输出算法. 但在实际问题中随机剖分数常依赖于模糊系统的逼近精度确定, 因此该输出算法具有一定局限性. 本文根据文献[12]给出的三角模糊化Mamdani模糊系统, 采用剖分论域和三角模糊化方法设计该模糊系统的输出算法, 并通过统计学的t-假设检验方法验证算法的有效性. 本文提出的输出算法与现有算法(如BP算法、 梯度算法、 遗传算法、 粒子群优化算法)不同, 现有算法通常是基于迭代公式和程序化设计和求解参数, 并采用仿真实验检验算法的有效性. 而本文输出算法是通过随机选取剖分数和寻找有作用的模糊规则设计算法, 其仅对基于三角模糊化的Mamdani模糊系统实施数值计算, 无需采用迭代公式求解模糊系统的调节参数.

1 预备知识

模糊系统输入(前件模糊集)在研究模糊系统的逼近性和稳定性方面具有重要作用, 而规范地输入变量可使模糊系统内部极大减少运算量. 特别当前件模糊集取值为三角形模糊数时, 所对应的Mamdani模糊系统应用广泛.

定义1[13]1) 设{A1,A2,…,AN}是论域U上定义的一族模糊集, 若∀x∈U, ∃i0∈{1,2,…,N}, 使得Ai0(x)>0, 则称模糊集族{A1,A2,…,AN}在U上是完备的, 即完备性要求论域U必须被所给模糊集的支撑集完全覆盖, 无空隙;

2) 设{A1,A2,…,AN}是论域U上定义的一族模糊集, 若∀x∈Ker(Ai)(i=1,2,…,N, 其中Ker(Ai)={x∈U|Ai(x)=1})均满足Aj(x)=0(j≠i), 则称{A1,A2,…,AN}在U上是一致的, 即一致性要求相邻模糊集之间必须相交, 但不能过界.

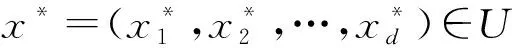
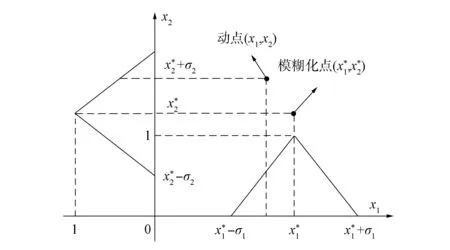
图1 n=2时三角模糊化示意图Fig.1 Schematic diagram of triangular fuzzifier when n=2

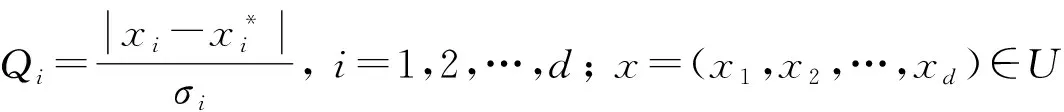
实际上, 模糊化就是将清晰输入变量转化为模糊数的运算过程, 即模糊化就是将实值点x*∈U⊂d转化为U上一个模糊集A′的过程, 或对一个清晰输入x=(x1,x2,…,xd)∈U进行模糊化变换Δ:U→F(U). 显然, 三角模糊化在峰值点x*处不仅满足A′(x*)=1, 且在x*点附近的隶属度取值可按A′(x)解析表达式计算, 但必须满足

Mamdani模糊系统的IF-THEN模糊规则如下:

其中:x=(x1,x2,…,xd)∈U⊂d为输入变量;Rm表示第m个模糊规则,m=1,2,…,M,M为规则总数;d为空间维数;为第m条规则在xi轴上的前件(输入)模糊集;Bm为第m条规则的后件输出模糊集;y是Bm的自变量且y∈V⊂;U和V分别为输入论域和输出论域.

实际上, 模糊推理机是将模糊规则库中若干规则合成为U到V上模糊集的一个映射. 通常模糊推理机有多种选择, 其中最常用的乘积推理机主要基于如下三条规则:

1) 利用模糊并组合的独立推理;

2) 基于Mamdani表示的乘积QML(x,y)=FP1(x)·FP2(y);

3) 所有t-范数算子选取代数积, 所有s-范数算子选取算子∨.

根据三条规则和文献[13], 论域U上的乘积推理机公式为

其中：x=(x1,x2,…,xd)∈U⊂d;A′(x)为经三角模糊化后的隶属函数;Bm为第m条规则对应的后件输出模糊集,m=1,2,…,M;B′为输出论域V上的整体输出模糊集.

解模糊化是指由V⊂上输出模糊集B′向清晰点y*∈V转化的过程, 而中心平均解模糊化是目前研究模糊系统中最常用的一种解模糊化方法.

定义3设A为上的模糊集, 若隶属函数A(x)在上达到最大值所有对应点的均值有限, 则称该均值为模糊集A的中心; 若该均值为+∞(或-∞), 则所有达到最大隶属度值中最小(或最大)点称为模糊集A的中心. 此外, 若隶属函数A(x)在上有最大值h, 则h称为模糊集A的高度.

基于此, 可按模糊化、 推理机和解模糊化步骤构造合适的模糊系统, 并处理一些信息不完整或未知函数表达式的逼近问题.

2 Mamdani模糊系统的输出算法

通常模糊系统可近似表示某些信息不完整的未知函数, 而该未知函数在论域内所有点或局部点的取值(数据对)可被获知, 但其解析式未知. 一般在给定数据对条件下可按模糊化、 推理机和解模糊化步骤构造模糊系统, 且其在紧集上可按任意精度逼近某个未知函数[11-15]. 此外, 由于通过线性变换y=(x-a)/(b-a)可将闭区间[a,b]变换为[0,1], 故只需在单位紧集[0,1]d上讨论模糊系统即可. 因此, 本文将根据文献[12]构造的Mamdani模糊系统设计输出算法.

设d维输入空间中每个xi轴上剖分数分别为Ni, 其中i=1,2,…,d, 并假设f在紧集U⊂d上连续, 且∀x∈U都有确定取值f(x)(相当于给定一个数据对(x;f(x))), 但函数f的解析式未知. 根据文献[12], 若选取前件模糊集为一致完备标准的三角形模糊数, 则按三角模糊化、 乘积推理机和中心平均解模糊化构造的Mamdani模糊系统输出表达式为

(1)

Mamdani模糊系统的输出表达式(1)包含很多参数和复杂运算, 如何选择这些参数至关重要. 为简单, 本文仅在前件模糊集取值为一致标准完备的三角形模糊数时, 给出Mamdani模糊系统的一个输出算法, 步骤如下:

1) 剖分论域. 在d维输入空间中每个坐标轴xi(i=1,2,…,d)的闭区间[0,1]上进行Ni等距剖分, 分点为j/Ni(j=1,2,…,Ni), 相应剖分数为N1,N2,…,Nd, 剖分后每个轴上小区间长度均为1/Ni; 再依次过每个分点做垂线, 即可获得论域空间[0,1]d的一个等距剖分.

图2 n=2时[0,1]×[0,1]上6×5等距剖分示意图Fig.2 Schematic diagram of 6×5 equidistant subdivision on [0,1]×[0,1] when n=2

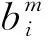
3) 确定有作用的规则数. 根据输入变量(x1,x2,…,xd), 通过做垂线确定每个分量xi在所属小区间有作用的三角形模糊数及其交点个数, 令ci(xi)表示分量xi对应的交点个数,i=1,2,…,d, 则实际有作用的模糊规则总数

M=c1(x1)×c2(x2)×…×cd(xd).

图3 Mamdani模糊系统的输出算法流程Fig.3 Flow chart of output algorithm of Mamdani fuzzy system

3 实例分析

下面在二维空间中通过选取实例和样本点给出上述算法的计算过程, 为方便, 把所给数据对的条件放宽为已知函数f(x)的解析式.

例1设二元函数

若前件模糊集的隶属函数选取三角形模糊数, 试通过上述算法分析Mamdani模糊系统在样本点处的输出值.

其中A0(x1)和A6(x1)分别是x1轴上以端点0和1为峰值点的半三角形隶属函数. 此时, 若将隶属函数A1(x1)在[0,1]上逐次向右平移1/6个单位长度直至右端点, 即可得其余4个模糊集A2,A3,A4,A5的隶属函数, 即令

Ak1(x1)=A1(x1-k1/6),k1=1,2,3,4.

不难获得一致完备标准的前件模糊集族{Ak1}, 参见图2.

同理, 在x2轴[0,1]上也可获得一致完备标准的前件模糊集族{Bk2}, 其隶属函数为

若令

Bk2(x2)=B1(x2-k2/5),k2=1,2,3,

则将B1(x2)向上依次平移1/5个单位长度, 也可在x2轴[0,1]上得到一致完备标准的前件模糊集族{Bk2}， 参见图2.

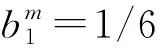
另一方面, 根据题设所给f解析式不难计算f(0.45,0.65)≈0.068 647 53, 显然, 二者误差较小.

下面通过小样本检验Mamdani模糊系统F(x1,x2)和实际函数f(x1,x2)的输出值和误差. 在[0,1]×[0,1]上随机选取30个样本点, 并通过MATLAB软件按F(x1,x2)和f(x1,x2)的解析式分别计算样本点的取值及其误差, 结果列于表1.

表1 F(x1,x2)和f(x1,x2)在30个样本点的输出值及误差

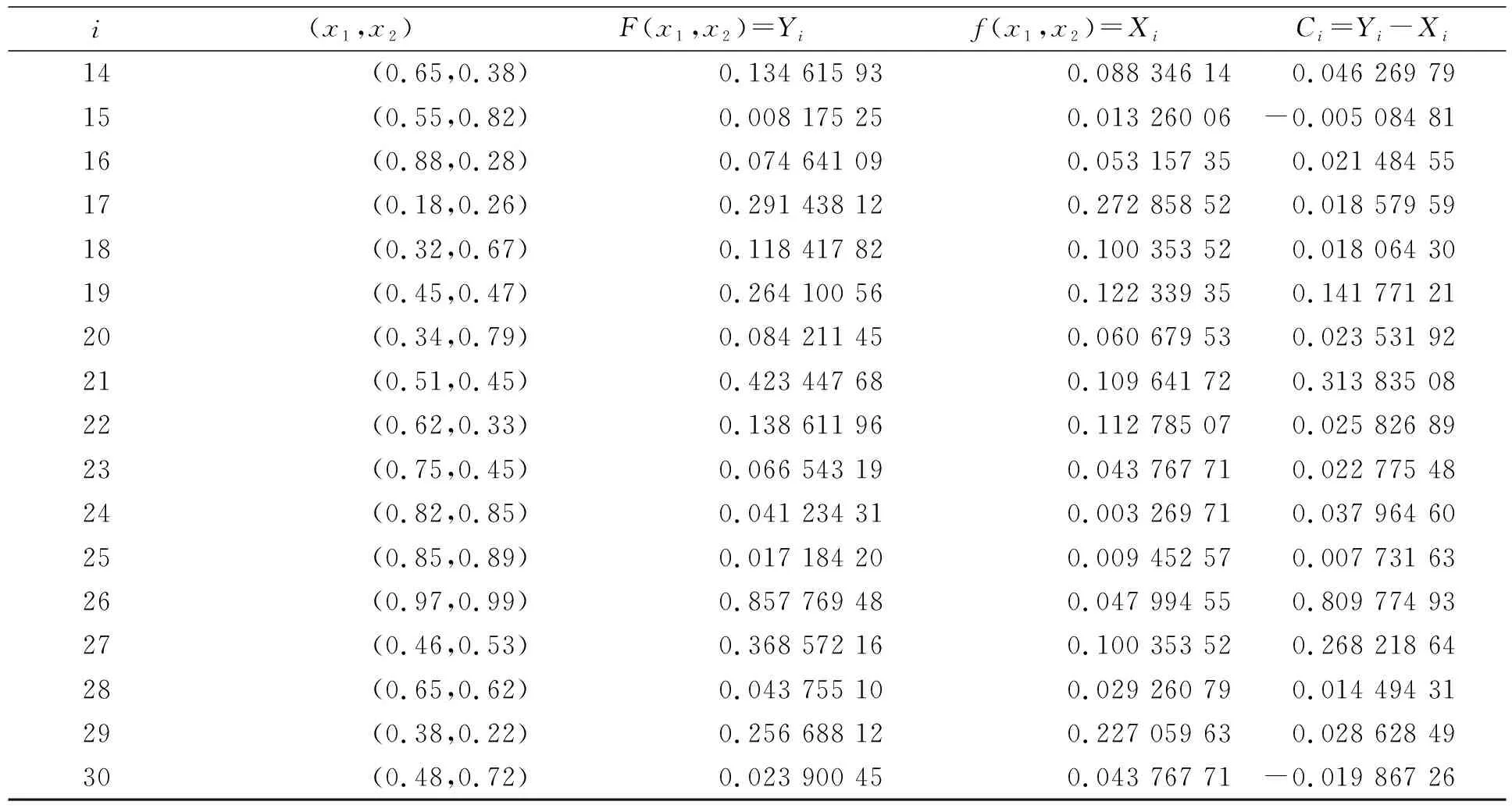
续表1

由表1可见, 函数F(x1,x2)和f(x1,x2)在顶点坐标处的取值均相同, 其误差值Ci均为零, 即它们在顶点处逼近效果最佳, 而在其他边界点或内点上逼近效果稍差. 下面利用统计学中的t-假设检验方法说明基于三角模糊化的Mamdani模糊系统具有逼近性.

对表1中误差数据Ci进行假设检验, 并在显著性水平α=0.05下检验假设{H0,H1}, 其中:

H0:μD≤0;H1:μD>0.

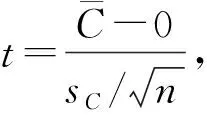
tα(n-1)=t0.05(29)=1.699 1.

故有

此时, 由于观察值位于拒绝域内, 故在显著性水平α=0.05下拒绝H0. 根据统计学t-假设检验方法说明该算法有效, 即基于三角模糊化的Mamdani模糊系统具有逼近性.

综上所述, 本文在文献[12]中Mamdani模糊系统解析式的前提下, 通过适当剖分论域和三角模糊化方法设计了Mamdani模糊系统输出算法, 并通过统计学原理验证了该算法的有效性.