基于有限元的杆端关节轴承结构优化

摘要： 针对某型号杆端关节轴承在疲劳试验时发生断裂的问题，对其原结构进行有限元仿真分析，得到的最大应力位置与实际断裂位置吻合，圆柱段仿真结果误差与应力理论计算结果仅为0.5%，验证仿真结果的可靠性。对杆端体各结构参数依次进行单变量有限元仿真分析，获取各参数对杆端体最大应力和质量的影响，据此确定优化顺序并对关节轴承进行优化。优化后的杆端关节轴承质量增加9.8%，最大等效应力降低14.9%，计算疲劳寿命从500万次提高到4 600万次，大于目标疲劳寿命值3 000万次，优化后的样件均顺利通过疲劳试验。

关键词： 关节轴承; 优化; S-N曲线; 疲劳寿命; 有限元

中图分类号： TH133.3;TB115.1   文献标志码： B

Abstract： As to the failure problem of a type of rod end spherical bearing in fatigue test， the finite element simulation analysis on the original structure is carried out. The position of the maximum stress by simulation coincides with the actual fracture position， and the error between the simulation result and the theoretical calculation result is only 0.5%， which can verify the reliability of the simulation results. The finite element simulation analysis on single variable is carried out for each structural parameter of rod end body in turn， and then the influence of parameters on the maximum stress and mass of rod end body is obtained. Based on these， the optimization sequence is determined and the spherical bearing is optimized. The mass of optimized rod end spherical bearing increases by 9.8%， and the maximum equivalent stress reduces by 14.9%， the calculated fatigue life increases from 5 million times to 46 million times， which is greater than the target fatigue life （30 million times）. All of the optimized samples pass the fatigue test successfully.

Key words： spherical bearing; optimization; S-N curve; fatigue life; finite element

0 引 言

杆端关节轴承是一种安装于杆端的球面滑动轴承，其转动和摆动不受约束，主要承受拉、压载荷，被广泛应用于航空航天、工程机械和铁路机车等领域的操纵和动力传递系统中。[1-3]杆端关节轴承一般包括桿端体和关节轴承2个部件，其中杆端体的主要失效模式为疲劳断裂，关节轴承的主要失效模式为磨损。[4-6]对杆端关节轴承施加载荷谱载荷，虽然杆端体最大应力小于材料抗拉强度，但是在多次应力波动变化后，杆端体局部产生疲劳裂纹从而断裂破坏。关节轴承磨损主要是由于轴承内圈相对外圈或衬垫转动或摆动，导致游隙增大甚至内、外圈分离等问题，使得接触面表面质量变差从而不满足质量要求。某型号直升机将杆端关节轴承安装于主旋翼控制系统中，受拉、压载荷频率较高，存在疲劳断裂风险，且失效后果极其严重，因此对该杆端关节轴承进行结构优化，提高其疲劳寿命。

1 杆端关节轴承结构

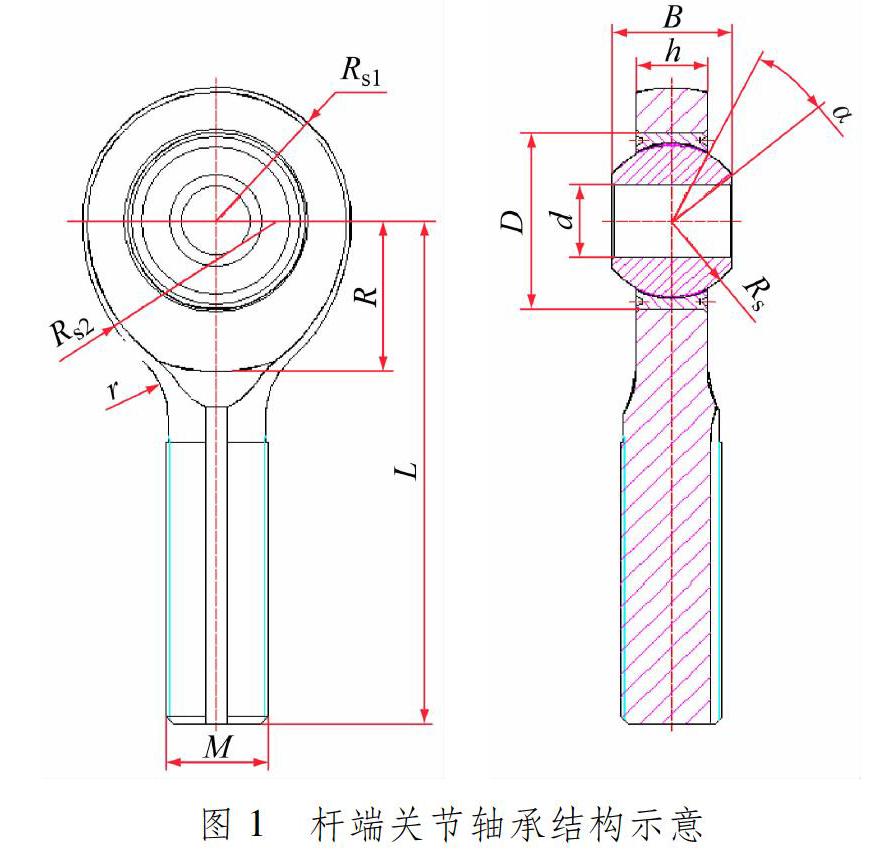
该型号杆端关节轴承结构见图1，包括杆端体、关节轴承外圈、自润滑衬垫、关节轴承内圈等。

根据结构特征，杆端体结构分为套圈段、螺纹段和过渡段3个部分。套圈段上半部分为Rs1球面，下半部分为以Rs2为母线的旋转体，Rs2大于Rs1且不同心。套圈下半部分外形近似椭圆形，因此该类杆端体也称为椭圆形杆端体[7]。M为螺纹接口直径，L为拉杆整体长度，内圈内径d和宽度B为销轴安装尺寸，α为内圈摆动角度，这些尺寸均为固定尺寸，结构优化设计中应保持不变。因为轴承内圈摆动角度α、内圈宽度B和内径d取固定值，受轴承最小厚度和内圈端面最小厚度的约束，内圈球径Rs和外圈外径D的可变范围极小，所以也取固定值。因此，影响杆端体应力分布的结构参数主要有过渡圆角半径r、杆端体套圈上半部分球径Rs1、杆端体套圈下半部分母线Rs2和杆端体套圈厚度h。修改这些参数进行杆端体结构优化，使杆端关节轴承在质量增加较小的前提下，获得最大的应力减小。关节轴承外圈与杆端体铆压装配对杆端体应力有一定影响[7]，但本文在同等装配条件下优化杆端关节轴承，因此可以忽略装配对杆端体应力的影响。

2 有限元仿真和验证

2.1 仿真模型

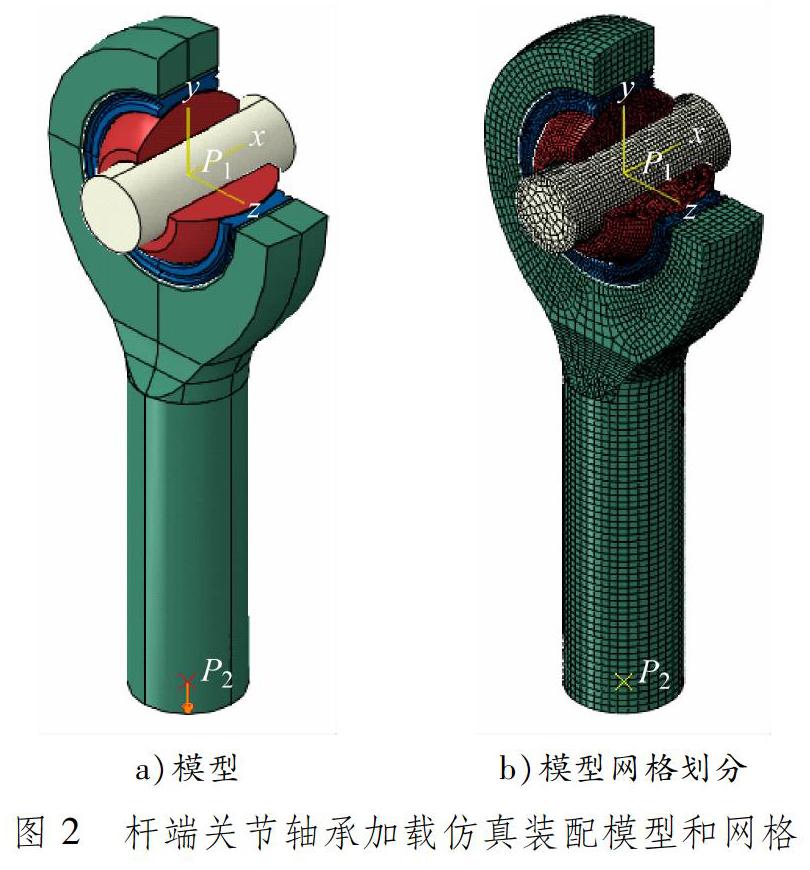
在Abaqus中建立杆端关节轴承与芯轴装配模型，见图2。芯轴两端与参考点P1耦合，并在耦合点施加6个自由度固定约束。杆端体下端面与参考点P2耦合，并施加30 kN拉载荷。零部件之间接触区域建立面-面接触对，法向接触属性为硬接触，切向接触摩擦采用罚函数法计算。钢对钢的摩擦因数为0.15，钢对自润滑衬垫的摩擦因数为0.06。材料参数设置为线弹性材料，弹性模量为206 GPa，泊松比为0.28。模型网格仅在杆端体圆柱底部的小区域用四面体单元，其他均为六面体单元，单元总数为82 626个，并确保接触对之间的主面单元略大于从面单元[8]。

2.2 初始关节轴承结构仿真

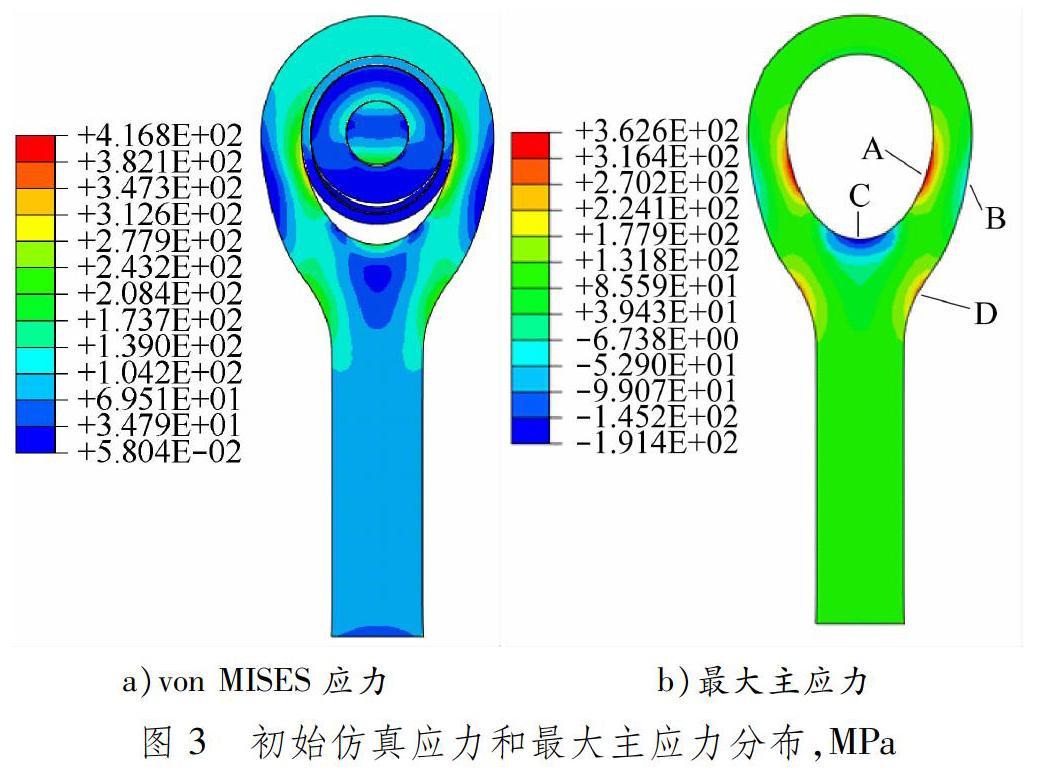
根据上述仿真模型，杆端关节轴承初始结构在拉载荷作用下的von MISES应力和最大主应力（变形量放大100倍）分布见图3。杆端体套圈下半部分沿载荷方向被拉长，杆端体套圈内孔与轴承外圈分离产生缝隙。由于杆端体套圈由圆形被拉伸成椭圆形，杆端体套圈内孔两侧（A区域）曲率半径增大，有被拉直的趋势，并且此处承受拉载荷，所以该处应力最大且为拉应力，大小为354.8 MPa。由最大主应力分布可知，该处最大主应力为357.5 MPa。相反，杆端体套圈外表面两侧（B区域）随着材料变形受挤压，但是与此处的拉载荷相互抵消，因此应力较小。杆端体套圈内圆柱面底部（C区域）曲率半径变小，材料受挤压，因此为压应力。过渡倒角（D区域）在载荷作用下曲率半径变大，并且此处承受拉载荷，因此材料拉伸变形，应力较大。

由上述初始结构仿真结果分析可知，在拉载荷作用下，杆端关节轴承变形主要发生于杆端体，轴承应力明显低于杆端体应力。杆端体最大应力位于套圈内孔两侧（A区域）且为拉应力，该处为杆端关节轴承疲劳寿命薄弱点，文献[1]中杆端关节轴承断裂分析也可验证该结果。因此，杆端关节轴承疲劳寿命结构优化的主要任务是改善套圈内孔两侧位置（A区域）抵抗变形的能力。

2.3 仿真结果验证

在拉载荷下，圆柱段受到均匀拉力，其理论应力σ=F/S=95.50 MPa（1）  由图3可知，该圆柱段应力仿真结果为95.98 MPa，仿真结果与理论计算结果误差仅为0.5%，验证仿真结果的准确性。杆端体套圈内孔两侧应力最大，但由于该位置在受拉载荷的同时还受弯矩载荷，该处横截面上应力分布不均匀，很难通过理论计算获得，因此应用有限元仿真方法进行优化。

3 有限元结构优化

不同结构参数对杆端关节轴承的应力和质量的影响不同。为分析杆端体各结构参数对杆端体最大应力和质量的影响，分别对过渡圆角r、上半圈外径Rs1、下半圈母线Rs2、平直段长度L和套圈厚度h进行单变量多水平仿真分析。每次仿真分析时，除当前分析变量取值变化外，其他结构参数均取初始结构参数值，仿真结果见图4。

由图4可知，不同结构参数对轴承质量和最大应力的影响不同，且同一变量的不同取值对结果影响也不同。单变量优化可以避免多变量耦合的影响，在实际产品优化过程中还可以减少工艺变更和变量验证等工作。但是，单变量优化无法达成目标或质量代价较大时，就需要依次优选“效率高”的变量进行优化，以最小的质量代价获得目标应力水平。

在本算例中，根据单变量优化结果曲线可确定优化顺序和优化取值依次为r=20 mm、Rs2=42 mm、L=5 mm、Rs1=27.5 mm、h=15 mm。按照上述优化次序进行优化，得到的轴承质量和最大应力结果见表1。

以单位质量可以引起的应力值减小作为优化效率，将单变量优化效率和顺序优化效率进行对比分析（见图5），两者变化趋势一致，优化效率依次降低。因此，根据单变量优化结果进行顺序优化，可确保关键结构参数优先被优化。

4 疲劳试验和分析

对初始状态杆端关节轴承进行单向拉伸疲劳试验，最大载荷为30 kN、最小载荷为3 kN，载荷偏差控制在2%以内，按正弦波加载，载荷频率为4.3 Hz。疲劳试验结果见图6，4个杆端关节轴承试验件在试验过程中均发生疲劳断裂，断裂位置均位于杆端体套圈侧面位置，与图3仿真分析结果杆端体套圈两侧最大主应力最大相吻合。4个杆端关节轴承试验件的平均疲勞寿命为500万次，与产品疲劳寿命目标3 000万次的差距很大。在不改变材料、工艺和装配方式的条件下，为达到目标寿命要求，必须对杆端体结构进行优化。

根据文献[9]中0Cr17Ni4Cu4Nb材料在4种工况下的高周疲劳数据，可以得到该材料的S-N曲线。由于加工过程材料组织变化、杆端体结构形状和表面粗糙度等均可对产品疲劳寿命产生影响，因此实际产品的S-N曲线往往位于材料S-N曲线的下方。根据文献[10]可知，材料S-N曲线与构件S-N曲线在对数坐标系下是平行的。因此，根据图6试验结果，通过平移材料S-N曲线，可获得实际杆端关节轴承产品的S-N曲线，见图7。由此可知，若要使疲劳寿命达到3 000万次以上，则应力应减小到326 MPa。根据前文顺序优化结果，当优化进行到第4步即可满足要求。当优化到第5步时，应力为308 MPa，疲劳寿命为4 600万次，此时质量增加9.8%、应力降低14.9%。

该型号产品经上述方法优化后，4个样件均顺利通过疲劳试验，验证优化的有效性。

5 结 论

在杆端关节轴承实际使用过程中，杆端体套圈疲劳断裂是其主要失效模式之一，据此对杆端关节轴承结构进行仿真优化分析，结论如下：

（1）利用Abaqus建立杆端关节轴承加载仿真模型，由最大应力位置和圆柱段应力，可验证仿真结果的可靠性。

（2）针对杆端体关键结构尺寸参数，分别进行单变量仿真分析，以单位质量对应力的影响值作为结构优化效率评价指标，认为杆端体中间过渡圆角r、杆端体套圈上半部分球径Rs1和杆端体套圈下半部分母线Rs2的优化效率较高，结构优化时应优先改善这3个参数。

（3）根据各参数优化效率对各优化参数进行排序，并按该顺序进行优化仿真，以避免参数之间的相互影响。按该顺序优化时，各参数的优化效率与单变量优化时的效率变化趋势一致。优化后杆端关节轴承的最大应力为308 MPa，比原结构降低14.9%，结构质量仅增加9.8%。

（4）基于杆端关节轴承疲劳试验建立结构件产品S-N曲线，基于该曲线预测，实现3 000万次疲劳寿命的应力为326 MPa，而优化结果应力为308 MPa时的疲劳寿命已经为4 600万次，满足寿命要求。通过优化，4个该型号产品样件均顺利通过疲劳试验。

参考文献：

[1] 苏高峰， 薄玉成， 孔静静， 等. 杆端向心关节轴承动应力下疲劳寿命分析研究[J]. 机械设计， 2013， 30（3）： 89-92. DIO： 10.13841/j.cnki.jxsj.2013.03.027.

[2] 李旭平， 蓝国水. 新型高速杆端关节轴承的寿命设计与试验研究[J]. 丽水学院学报， 2011， 33（5）： 49-51. DIO： 10.3969/j.issn.1008-6749.2011.05.013.

[3] 齐爱霞. 杆端关节轴承三维参数化计算机辅助设计与研究[D]. 青岛： 山东科技大学， 2006.

[4] 袁兆静， 刘红宇， 邵玉佳， 等. 杆端关节轴承杆端体的疲劳断裂机制[J]. 机械工程材料， 2018， 42（12）： 13-17. DOI： 10.11973/jxgccl201812003.

[5] 曾坤， 张韶佳， 陈昕， 等. 杆端关节轴承失效分析[J]. 失效分析与预防， 2018， 13（5）： 318-323. DOI： 10.3969/j.issn.1673-6214.2018.05.010.

[6] 艾剑波， 黄文俊， 李满福， 等. 直11型机尾桨变距拉杆故障分析与处理[J]. 直升机技术， 2009（3）： 68-71. DOI： 10.3969/j.issn.1673-1220.2009.03.014.

[7] 邱明， 吕桂森， 占松华， 等. 自润滑杆端关节轴承的摩擦性能研究[J]. 兵工学报， 2013， 34（6）： 754-758. DOI： 10.3969/j.issn.1000-1093.2013.06.015.

[8] 王启瑞. 基于Abaqus的GE17自润滑关节轴承结构分析与改进[J]. 计算机辅助工程， 2017， 26（4）： 51-56. DOI： 10.13340/j.cae.2017.04.009.

[9] 霍金东， 由小川. 基于能量法的17-4PH钢材疲劳特性研究[C]// 北京力学会第21届学术年会暨北京振动工程学会第22届学术年会论文集. 北京： 北京力学会， 2015： 374-379.

[10] 解放. 典型构件疲劳性能S-N曲线的获取及应用[J]. 机械设计， 2015， 32（4）： 71-73. DOI： 10.13841/j.cnki.jxsj.2015.04.015.

（編辑 武晓英）