外周动脉斑块钙化程度对血管内介入治疗的影响

郑清丽，吕 营，李志强，陈凌峰，安美文

（太原理工大学a.生物医学工程学院，b.机械与运载工程学院 应用力学研究所，c.材料强度与结构冲击山西省重点实验室，太原030024）

与冠状动脉斑块不同，外周动脉的斑块通常更为纤维化，并且可能含有大量的易于在血管中扩散的钙。外周动脉斑块破裂主要是由于斑块承受高应力作用，如脉动压、生理拉伸产生的结构应力及血流动力学作用下的壁面剪切力而导致斑块内几何形态和材料出现变化继而发生破裂［1］。对于外在荷载，如介入治疗过程中血管成形术及支架置入术对斑块的高应力作用同样是其破裂的重要因素：极易在治疗部位引发组织损伤导致斑块破裂引发栓塞，诱导炎症性免疫应答反应而增加血栓形成的风险，并且可能伴随着异常的平滑肌细胞增殖，使管腔内新生内膜和平滑肌层增厚，最终导致动脉再狭窄的发生［2］，因此斑块破裂是一个不可忽略的因素。钙化程度决定着斑块的力学性能，作为外周动脉主要分支的下肢动脉（特别是股动脉，FPA），斑块的钙化最为严重，尤其是同时患有糖尿病或慢性肾病的患者，由外周动脉疾病导致的死亡率是心血管疾病的2倍，截肢风险高达心血管的4倍［3］。但FPA钙化的病因尚不清楚，同时临床上对于具有不同钙化程度斑块的FPA介入治疗后生理机理、组织损伤风险及压力诱导的病理重塑机制缺乏相应的研究［4-5］。因此斑块钙化程度对介入治疗的影响也已成为外周动脉病变防治和治疗关注的重点。

目前虽然FPA支架置入后狭窄血管的通畅性得到改善，但临床数据显示FPA支架的通畅率仍然比大多数其他部位的动脉更差。这是由于FPA在肢体运动期间会经历大范围的机械变形，经常处在包括扭转、弯曲及压缩等在内的独特的高动态力学环境中。同时在外周动脉结构应力研究中，斑块与动脉管壁相连，现有技术无法测量动脉管壁上的残余应力，而残余应力对血管结构应力的分布有着重要的影响。目前只有少数研究考虑了残余应力的影响，若不考虑残余应力则斑块计算得到的易破裂部位峰值应力偏高［6］，因此考虑残余应力对于动脉研究有重要的意义。

针对以上问题，本文在模型建立的基础上，首先对动脉的残余应力进行了计算，然后在含有残余应力的健康动脉模型的基础上建立外周病变动脉（含钙化程度不同的斑块）模型，进一步分析支架球囊预扩张后病变动脉在肢体直立和运动下的受力状态，探索斑块的钙化程度对治疗结果的影响。

1 计算模型与方法

1.1 几何模型

1.1.1 动脉壁几何模型

健康动脉壁由3层组成，分别为内膜、中膜和外膜［7］，其厚度分别为0.15，0.25，0.10mm［8］，长度和腔内直径分别为50mm和5mm［9］，如图1（a）所示。对于有残余应变的管壁，选择张开角为90°［10］（图1（b）），模型的建立依据动脉壁张开前后管壁截面中性层长度不变。动脉粥样硬化病变血管由血管壁和附在血管壁上的斑块两部分组成，管腔的内径相当于健康血管的30%，即狭窄率为70%，可以充分地评估临床相关的动脉病变。代表动脉粥样硬化斑块长度为15mm，斑块中间位置处最大厚度为1.5mm，作为单一的几何实体，置入动脉内膜内，使健康和病变部分之间平滑过渡，从而形成与健康动脉相对应的动脉粥样硬化病变血管（图1（c））.

1.1.2 支架模型的构建

本文选择自膨式Wallstent支架，是由20根直径为0.1mm的Co-Cr合金丝（即Elgiloy）编织而成的管网状结构，其交叉点间的夹角为140°［2］.根据支架的选用规则，本文选取编号为H965SCH647070的支架，长度为21mm，直径为8mm，如图1（d）所示。

1.1.3 周围肌肉、压握装置及球囊模型的构建

在下肢运动过程中，股动脉完全包裹在紧致的肌肉中，其所处的高动态力学环境是由于肌肉的局部伸展收缩运动造成的。肌肉作为动脉的外部环境，对动脉起到约束作用［11］，为了保障计算的准确性，对周围肌肉的建模是必要的。本文中肌肉的长度跟血管相同为50mm，横截面为10mm×10mm，中间直径6mm的圆孔为动脉所处区域如图1（e）所示。本文选择非顺应性球囊，临床操作中球囊的长度不能超过斑块的长度，选取球囊长度为15mm，直径为0.8mm；压握装置要确保支架直径能够压握到1.2mm，取其长度为65mm，直径为8.2mm，两者均为圆柱形刚性管。

1.2 血管壁、斑块及支架材料属性

1.2.1 动脉壁材料属性

健康血管采用GASSER et al［12］提出各向异性超弹性本构模型（HGO模型），基于应变不变量的应变能密度函数，将血管作为一种纤维增强复合材料，包括每层内的纤维取向和纤维分散程度，具体参数见表1［13-14］.

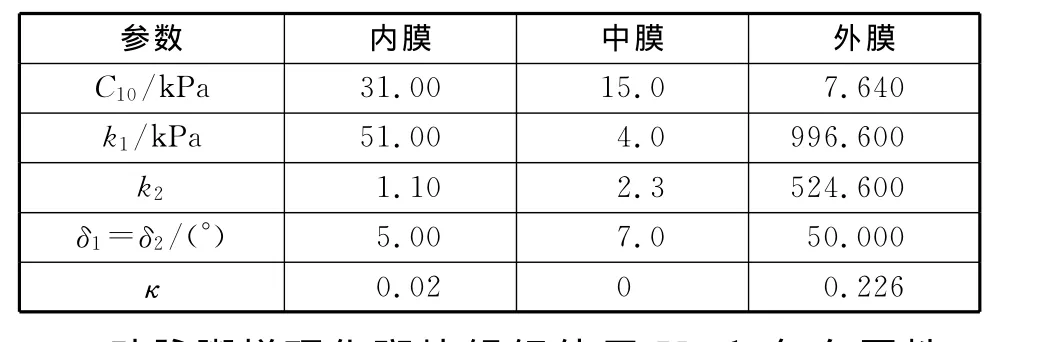
表1 血管材料属性Table 1 Material parameters of the artery

动脉粥样硬化斑块组织使用Yeoh各向同性3阶减缩多项式超弹性应变能函数，通过对20个动脉粥样硬化患者的股动脉斑块进行平面拉伸实验得出［15］，具体见表2.实验测定所有样本的钙锂比在1～3之间，对3种钙化程度不同斑块进行生物学特性分类是基于它们的钙锂比。这种分组方法旨在反映生物含量（Ca∶Li）和力学响应（刚度和极限强度）的分层，归因于其失效特性和失效发生路径趋势明显，详见图2［15-16］.

表2 斑块的材料属性及斑块组织在平面拉伸下的力学性能Table 2 Material parameters of calcified plaques and the mechanical behavior of the plaque tissue under planar tension tests

对于斑块失效性的研究采用塑性模型模拟组织损伤［17-18］，即斑块发生塑性变形时，一旦达到塑性极限，斑块发生损伤破坏，此时施加在其上的压力将不会增加，载荷转移到健康层；而在卸载时，斑块产生的塑性变形将不变，健康层中的应力取决于动脉粥样硬化组织中塑性变形的程度［19］。斑块塑性阈值对应斑块的破坏应力水平（见图2）.

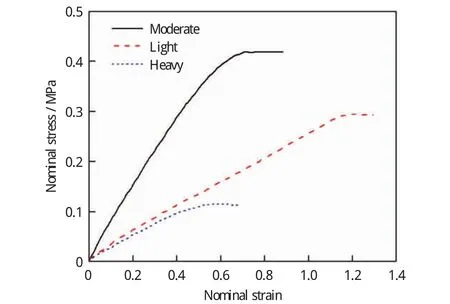
图2 斑块的平均应力-应变图Fig.2 Average stress-strain behaviors of the calcified plaques

1.2.2 支架、周围肌肉、压握装置及球囊的材料属性

对于编织自膨式 Wallstent支架，本研究中采用各向同性线弹性本构模型。其中材料密度为8 300kg／m3，弹性模量为194GPa，泊松比0.226，屈服强度为2 280MPa［20］.肌肉材料选用能够代表非线性弹性大变形的Mooney-Rivlin超弹性本构模型［21］。此前的研究表明，非线性超弹性模型最适合模拟肌肉和软组织，其中材料参数［22］为C10＝0.001 65 MPa、C01＝0.003 35MPa，D1＝0.49.压握装置及球囊则采用线弹性本构模型，弹性模量为210GPa，泊松比为0.3.

1.3 模型网格划分

本文研究的重点是斑块及动脉壁在扩张状态下的受力状况，为了得到较为精确的计算结果，需对斑块和动脉壁进行网格细化。上述模型各自对应不同的单元类型，同时对网格的收敛性进行了验证，具体模型网格的划分详见表3.

表3 模型网格划分Table 3 Model grid division

1.4 血管残余应力的设置

对于有残余应变的管壁，参照前人的实验研究结果选择动脉壁张开角为90°［23，10］。具体设置为在张开角两端面的外膜中点各建立一参考点（图3），将参考点通过coupling约束与切开的截面完全耦合，通过在参考点上施加径向、周向及绕动脉轴向方向的旋转位移，将处于零应力状态的血管闭合，从而获得血管残余应力，至此血管处于无荷载状态（Non-loaded state）.内膜、中膜和外膜间采用“Tie”绑定约束，同时当两参考点闭合时，剪开壁面两侧相对应的内膜、中膜和外膜分别设置面面接触（Surface-to-surface contact）。因血管的闭合是一个动态的过程，本文采用ABAQUS／Explicit求解器来计算模拟血管残余应力。

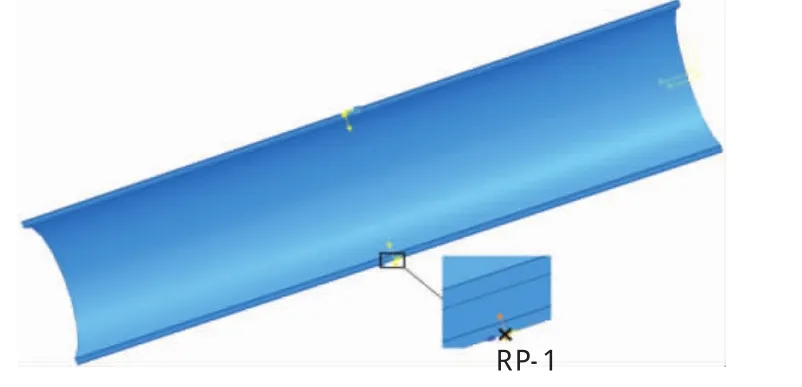
图3 参考点设置Fig.3 Reference points setup

1.5 数值计算及边界条件

支架球囊预扩张是指先用球囊扩张狭窄动脉后释放支架，肢体直立状态下支架球囊预扩张加载步骤为：

1）对放置于狭窄动脉内壁的球囊施加沿径向方向向外的位移，直到球囊的直径达到健康动脉的直径为止；

2）撤出球囊，对球囊施加与步骤1）相反的径向位移，此时斑块出现回弹；

3）对压握装置施加沿径向方向向内的位移，支架位于压握装置内，直到将支架压握到直径为1.2 mm为止；

4）撤出压握装置，对压握装置施加与步骤3）相反方向的径向位移，此时支架释放于狭窄动脉中，与动脉壁相互作用；

5）对斑块和健康动脉内壁施加法向方向的均布荷载（13.3kPa）用以模拟生理血压的作用。

肢体运动状态下支架球囊预扩张加载步骤是在直立状态设置的基础上，对动脉两端分别施加绕x轴方向的旋转角位移（40°）来模拟弯曲载荷，绕z轴方向的旋转角位移（12°）来模拟扭转荷载，如图4所示。动脉中斑块内表面和扩张装置之间设置为面面接触，采用硬接触确保了接触表面没有穿透，摩擦系数为0.25［24］.

图4 运动状态下动脉的有限元设置Fig.4 Finite element model of artery under in motion

2 结果分析与讨论

2.1 动脉残余应力分布

含有残余应力的动脉壁，其周向残余应力分布如图5（a）所示，周向应力与壁厚的关系如图5（b）所示，其中动脉的壁厚默认方向为内膜到外膜的厚度。

由图5中可以看出，张开角闭合后，动脉处于无荷载状态，此时内膜上为周向残余压应力，外膜上为周向残余拉应力，中膜靠近内膜区域为周向压应力，而与外膜连接处为拉应力，与HOLZAPFEL et al研究结论相符合［25-26］。中膜周向应力发展比较平缓，而内外膜应力梯度相对较大，外膜尤其突出。

2.2 支架受力分析

含有残余应力和钙化斑块的动脉，经球囊预扩张后置入支架，在下肢直立和运动状态时支架所受的应力如图6所示。在动脉中间最狭窄处支架的Mises应力最大，逐渐过渡到达端部时最小。直立状态下，置入到轻度、中度和重度钙化斑块中的支架最大 Mises应力分别为1 378，1 377，1 324MPa；运动状态时支架最大Mises应力分别为1 436，1 445，1 390MPa.支架所受应力相差很小，运动状态下应力略大于直立状态，这是因为在运动状态，动脉和支架同时受到弯扭作用，此时最大Mises应力位于动脉狭窄处支架下端受弯位置，均小于支架材料屈服 应力2 280MPa.

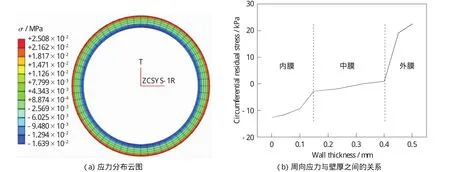
图5 动脉周向残余应力的分布Fig.5 Distribution of circumferential residual stress in arteries

图6 支架置入动脉后在直立和运动状态下应力云图Fig.6 Stress contours of stent after implantation in the upright and motion states of the artery

2.3 斑块应力分析

含有残余应力的病变动脉，在球囊预扩张后置入支架，斑块受到球囊和支架的双重扩张，产生一定的变形，本文中使用最大主应力（maximum principal stress）来计算斑块的应力水平。对于3种钙化程度不同的斑块，在肢体直立和运动状态下应力云图如图7（a）和图7（b）所示。

直立状态下，由于斑块中间狭窄部位比两侧厚，支架置入时中间部位形变量最大。三者中中度钙化的斑块所受的主应力峰值最大。轻度和中度钙化的斑块所受到的最大主应力中压应力峰值均出现在狭窄动脉两侧斑块与支架的接触处，最大主应力中拉应力峰值则出现在动脉最狭窄处斑块与支架接触的网孔之间。高拉应力与高压应力之间的高应力梯度会触发内皮细胞和平滑肌细胞作用机理发生变化，进而诱导信号传导通路发生变化。目前对能诱发斑块发生破裂的应力梯度没有统一定论，因此有必要对其进行深入的研究。中度钙化斑块中最大主应力（67kPa）高于轻度钙化斑块（53kPa），且其分布的范围相对较广。重度钙化的斑块应力分布正好相反，最大主应力中拉应力（28kPa）位于两侧狭窄处，斑块与支架接触的网孔之间，斑块与支架接触处均属于压应力区。

运动状态下时，动脉在弯扭作用下，3种钙化斑块的最大主应力均位于斑块两侧端部底部受拉区域。为了研究肢体运动时斑块最狭窄处的受力变化，如图7（b）所示选取斑块的中间区段进行比较。结果显示，中度钙化板块中主应力峰值仍最大。与直立状态相比，因斑块受到弯扭作用，运动状态下斑块的最大主应力开始向底部拉弯区域转移且数值增大，此时3种钙化斑块底部区域由直立状态时的最大压应力开始向运动状态时的拉应力转变。

综合比较直立和运动状态下斑块的最大主应力分布可以得出，位于底部区域处的斑块在肢体运动过程中，所受的最大主应力在压应力（直立）与拉应力（运动）间不断地转换，在循环载荷下，斑块一直处于疲劳状态［27］。当达到斑块的疲劳极限时，任何作用在它上的力都可能使其结构失效，导致在远低于临界应力的情况下毫无征兆地发生破裂［28］。

2.4 斑块塑性等效应变分析

塑性等效应变（PEEQ）描述的是整个变形过程中塑性应变的累积，一旦达到塑性极限，斑块发生损伤破坏，当塑性等效应变达到斑块的塑性阈值时，施加在斑块中应力将不会增加，载荷将转移到相连的动脉中。

3组钙化程度不同的斑块在支架球囊预扩张后，其塑性等效应变（PEEQ）分布如图8所示。从图中可以看出，最大等效塑性应变均发生在斑块的中间最狭窄处，重度钙化的斑块在直立和运动状态下均具有最高的塑性应变值（1.232），归因于重度钙化的斑块塑性变形过程中所需的低应力和应变阈值，同时也表明支架置入含重度钙化斑块的动脉中狭窄率最小，轻度钙化斑块塑性应变值（0.959）最低，中度钙化斑块的塑性应变值（1.055）介于两组之间，3组钙化斑块在运动状态下的塑性等效应变值均小于其直立状态下。

2.5 血管的受力分析

关于支架置入后动脉管壁受力研究，不少学者发现最易发生损伤破坏的是外膜，其失效应力约为1 300kPa，中膜的应力仅达到组织极限拉伸应力15%［8］，因此选取外膜进行受力分析。

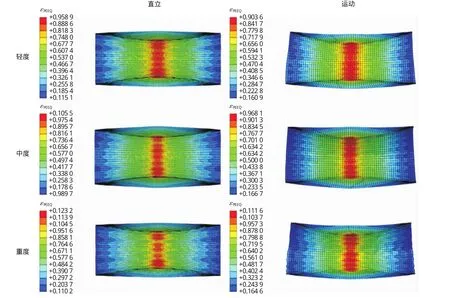
图8 斑块塑性等效应变分布图Fig.8 PEEQ distribution of the calcified plaques

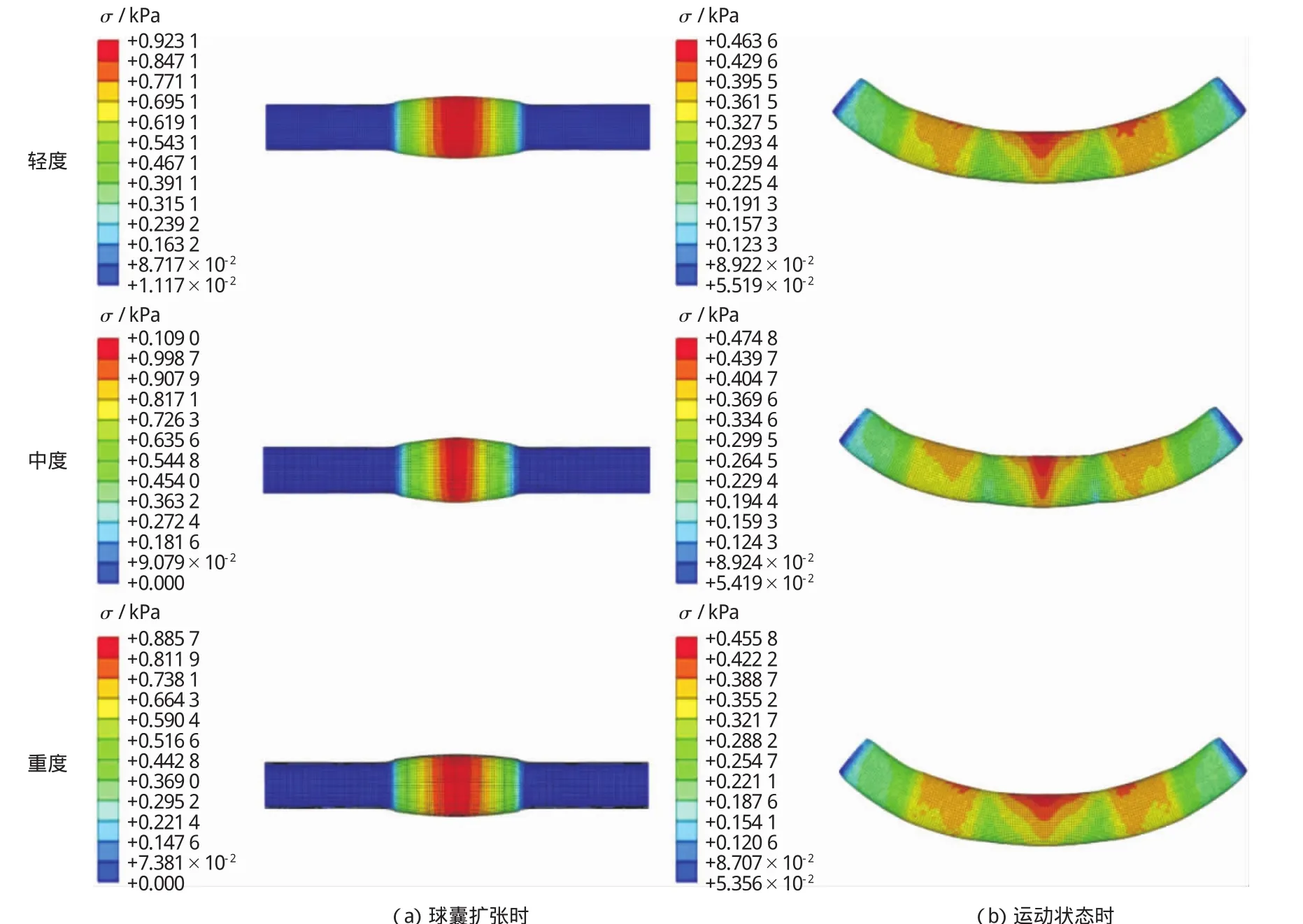
图9 外膜的应力分布Fig.9 Distribution of stress of adventitia

图9 为3种钙化程度不同斑块的外膜在球囊扩张时最大周向应力分布图（左）和支架置入后运动状态下最大正应力分布图（右）。因球囊长度不能大于斑块的长度，球囊预扩张时，周向应力集中分布于动脉的中间位置处，轻度、中度和重度钙化斑块所在外膜周向应力分别高达其失效应力的71%，83.8%，68.1%，相比较而言中度钙化斑块外膜更易发生破坏。因此在选用球囊直径时不宜过大，球囊直径与动脉直径比例应控制在1.4以下为宜［8］。同样在运动状态下，三者外膜最大主应力均发生在斑块狭窄中间及两侧支架与健康内膜接触处，运动状态时因动脉两端部受到弯扭作用，作用力由两端向中间部位传导，支架与健康动脉接触的应力开始变大，此区域极有可能最先出现损伤，发展为动脉粥样硬化。中度钙化的斑块所在的动脉在直立和运动状态时均具有最大正应力且分布在斑块中间区域，之所以会出现此现象，是因为中度钙化的斑块强度较高，球囊扩张下在径向方向上移动相同的位移时，斑块受到的应力较大，相应地传递到健康动脉上的应力也增大。

2.6 讨论

血管介入治疗支架的失效是临床中亟需解决的一个关键问题。从医疗器械设计的角度来看，需要知晓不同部位动脉的力学环境以及球囊扩张和支架置入过程中与动脉粥样硬化组织间的相互作用，在对动脉力学环境及动脉粥样硬化病变血管材料精确掌握的基础上，才能够更好的利用有限元研发出更专业和合理化的介入支架，有针对性的在临床中选取不同的治疗策略。然而，股动脉斑块组织相较于其他部位的斑块，钙化相对比较严重，含钙量直接影响到其生物特性及整体力学性能［29-30］。因此在植入支架时能够对钙化程度不同的斑块组成成分及力学性能有所了解，能够对支架植入与斑块的相互作用和潜在斑块破裂的位置等有所判断和评估，可为临床治疗策略提供指导。

本文中采用塑性准则作为斑块的失效准则，斑块的破裂一般是在高水平应力作用下斑块的组成材料及几何形态等均发生变化，且处于长期的疲劳作用下发生的。目前运用有限元研究斑块破裂的关键参数之一是最大主应力的大小和位置，此为判断患者特定动脉粥样硬化斑块破裂风险的直观因素，同时也突显了此类研究对诱发破裂应力阈值选择的依赖性。关于破裂阈值的选择目前使用最多的是300kPa［31］，斑块到达该阈值时发生破裂可引发致命性心肌梗死。有研究者认为这个阈值是斑块从稳定性到不稳定的过渡［32］，处于钙化不同时期的斑块应力及稳定性所对应的阈值有所不同，发现破裂斑块的平均最大应力为（545±160）kPa，稳定斑块的平均最大应力为（193±65）kPa［31］.MALDONADO et al［33］则对斑块进行了力学分析，认为如果没有微钙化，薄的未破裂纤维帽中的最大周向应力仅为107kPa，远远低于建议的300kPa最小破裂阈值。不同动脉系统的形态和力学特性之间差别很大，因此对于阈值的判定需根据斑块特定位置选取阈值，而不是一个阈值适用所有位置。动脉残余应力对斑块的形成和发展同样有着重要的影响，如动脉壁残余应力可对纤维帽施加正向挤压应力，而管腔内脉动的血压则对纤维帽施加反向挤压应力，基于这种理论认为斑块的破裂是由于血压外荷载和自身残余应力失衡的结果［34］。因此本文在进行有限元计算时将含有残余应力的动脉作为初始条件，对3组不同斑块的动脉受力进行综合研究。

本文中未考虑直径不同的球囊对狭窄动脉的扩张。已有研究发现正常大小的球囊更有利于保护动脉壁免受慢性损伤，使用大直径球囊扩张时，动脉所受的最大周向应力与管腔直径的增加是非线性的。当球囊过大时，扩张时动脉最大周向应力迅速增加，然而释放球囊后管腔直径的增加却不显著［8］。另本文中支架采用自膨胀支架，具有良好的贴壁性能，故未考虑贴壁性能的影响。

3 结论

通过在设置计算得残余应力动脉的基础上，将支架置入到含有轻度、中度和重度钙化斑块的动脉中，研究斑块和管壁的受力状态，用以评估斑块钙化的严重程度对病变动脉的影响，主要结论有以下几个方面：

1）含有残余应力动脉内膜上存在周向压应力，外膜上为拉应力，且内外膜应力梯度较大。

2）支架置入到含有残余应力和斑块钙化程度不同的动脉时，其所受到的应力相差很小，均未达到支架材料屈服应力。

3）3种钙化斑块中，中度钙化斑块的主应力峰值最高；位于底部区域处的斑块在肢体运动过程中处于疲劳状态，当达到疲劳极限时，斑块极有可能结构失效发生破裂。3组斑块的最大塑性等效应变均发生在斑块的中间最狭窄处，严重钙化的斑块在直立和运动状态下均具有最高的塑性应变，狭窄率最低。外膜为动脉扩张中最易破裂的部位，尤其以中度钙化的斑块所在动脉最为危险，其中最易发生动脉粥样硬化增生的部位位于动脉最狭窄处及支架与 健康动脉相接触的位置。