基于流-固耦合理论的水体下盾构隧道施工渗流规律
郤保平,陈路海,董赟盛
(1.太原理工大学a.矿业工程学院,b.原位改性采矿教育部重点实验室,太原030024;2.济南城建集团有限公司,济南250000)
随着水下隧道工程建设技术日趋完善,水下盾构隧道已经成为跨越水域的重要交通工程之一。在隧道工程施工过程中,由于存在着稳定的补给水源,渗流场和应力场相互作用、相互联系,使得隧道围岩孔隙压力发生变化,隧道围岩极易发生失稳,造成严重的工程事故。
近年来,国内外许多学者对隧道施工过程中流-固耦合问题进行了研究。YI et al[1]通过数值模拟研究分析了盾构隧道开挖后孔隙水压力和地层沉降的分布规律;GALLI et al[2]对二维模型和三维模型计算结果进行了对比,认为三维模型更加符合工程实际;纪佑军等[3]采用数值模拟,认为注浆可以有效控制隧道围岩变形和地下水涌入;原华等[4]通过对上海越江隧道东线中段的数值模拟分析,得出管片在渗流作用下的受力更加趋于“平均”,地下水有利于隧道衬砌管片的受力;吉小明等[5]通过分析渗流作用下隧道开挖过程发现,隧道周边最大剪应力和位移都有所增大;马龙祥等[6]假设当软土盾构隧道达到稳定渗流状态时,作用于衬砌外壁的总水头为一个未知常量,计算出稳定渗流时隧道的闭合解析解;易小明等[7]通过对比分析流-固耦合作用下海底隧道开挖数值模拟的结果与现场监测数据,认为两者具有一致性;贾瑞华等[8]通过数值模拟分析得出了隧道开挖面处的渗流场、位移场以及孔隙水压力的分布规律。然而,国内外对高水头压力作用时盾构隧道施工扰动下地表的沉降量、围岩渗透性、管片内力分布等方面的研究并不多。近几年来,穿越江、河的盾构隧道工程越来越多。因此,研究高水头压力作用下盾构隧道的地表沉降、孔隙水压力分布、施工扰动下围岩的渗透性以及隧道衬砌管片的受力特征,对于盾构隧道施工及运营期间的安全稳定具有重要意义。
本文选取太原地铁2号线双塔西街—大南门站下穿迎泽湖区段为工程背景,采用有限差分软件FLAC3D内嵌的FISH语言二次开发建立三维数值模型,得出不同水头压力作用下的盾构隧道在流-固耦合效应下的渗流场、位移场以及管片衬砌的孔隙水压力的分布规律,以期为水下隧道施工工程风险控制提供理论依据和技术支持。
1 流-固耦合数学模型
在建立岩土体流-固耦合数学模型时,规定岩土体为等效连续介质,同时流体在岩土体中的运移满足达西定律以及Biot固结方程。流-固耦合数学模型涉及的方程有以下几种[9-12]。
1.1 运动方程
流体的渗流运动可用达西定律来描述。均质、各向同性的固体以及常密度的流体的渗流量q用达西定律可表示为:

式中:k为介质的渗透系数,m2/(Pa·s);p为孔隙水压力,Pa;ρw为流体密度,kg/m3;xj为三个方向上的距离梯度;gj为重力加速度的分量,m/s2.
1.2 流体质点平衡方程
小变形情况下,流体质点平衡方程为:

式中:qi,i为渗流体单位消散矢量,m/s;qv为被测体积的流体源强度,s-1;ζ为单位体积孔隙介质的流体体积变化量。
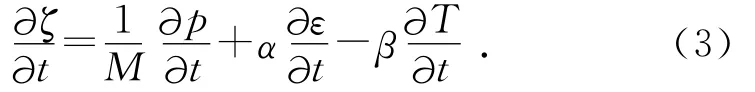
式中:M 是Biot模量,N/m2;p 为孔隙水压力,Pa;α为Biot系数;ε为体积应变;T为温度,K;β为考虑流体和颗粒的热膨胀系数,K-1.
动量平衡方程的形式为:

式中:ρ为密度,kg/m3;gi(i=1,2,3)为重力加速度的分量,m/s2.其中,ρ=(1-n)ρs+nρw,ρs和ρw分别为固体和液体的密度,n为多孔介质的孔隙率。基体的干密度ρd=(1-n)ρs,ρ=ρd+nρw.
1.3 本构方程
体积应变的发生会导致孔隙水压力的改变,而孔隙水压力的改变又会再次引起体积应变的发生,二者相互作用,相互影响。故孔隙介质本构方程的增量形式表现为:

式中:Δσij为应力增量;Δp为孔隙水压力增量;δij为Kronecher因子;Hij为给定函数;Δξij为总应变增量。
1.4 相容方程
总应变与速度梯度之间的关系可表示为

式中:ξij为总应变;v为介质中某点的速度,m/s.
1.5 边界条件
FLAC3D有限差分软件提供4种边界条件:透水边界;不透水边界(程序中默认为不透水边界);定孔隙水压力;给定边界外法线方向的流速分量。其表达方式为:

式中:qn为边界外法线方向的流速分量;h为漏失系数,m3/(N·s);p为边界处的孔隙水压力;pe为渗流出口处的孔隙水压力。
FLAC3D有限差分软件包含上述构建模型所需的所有公式。因此,只需设定软件自带的 Mohr-Coulomb屈服准则及合理的计算模式,输入计算所需要的土体和流体相关参数,就可进行水下盾构隧道流-固耦合数值模拟分析。
2 工程应用
2.1 工程概况
太原地铁2号线双塔西街—大南门站下穿迎泽湖,属于典型的富水区域,该区段采用土压平衡盾构法施工,设计隧道埋深为18m,内、外径分别为5.5 m和6.2m.迎泽湖水深约5m,宽度30~50m,穿越地层岩性主要为粉细砂土、中砂土层。起止里程:左线为ZCK22+695.000~ZCK22+851.000,长约148m;右线为 YCK22+695.000~YCK22+851.000,长约162m.左、右线隧道相距14.2m.
2.2 物理模型建立
土体为无限体,考虑到边界效应的影响,隧道施工后土体应力重分布的范围为隧洞洞径的3~5倍。所以,数值模拟隧道模型的计算范围为:垂直方向上部为隧道上覆岩土层厚度,即拱顶至湖底表面的长度;下部沿隧道中心向下取4D(D为隧道的内径),水平方向向外各取5D[13-14],轴向方向取该区段湖底隧道的实际长度,即156m(长)×77m(宽)×46m(高)。模型共划分为244 332个节点、237 640个单元,采用软件内置摩尔库伦弹塑性模型构建各土层以及注浆层单元,衬砌管片则采用shell单元,如图1所示。
盾构隧道开挖流程如图2所示。首先,去除开挖面该时步所需开挖地层单元,添加管片单元来模拟开挖面支护,生成新一层开挖面支护应力。其次,停止FLAC3D中的流体渗流计算部分,只计算模型在力学作用下土体不排水变形量,通过迭代计算使模型达到不排水状态下的平衡,然后加入流体渗流场,采用流-固耦合模式计算该环土体在开挖时间内的排水变形量。该时步耦合计算完成后,进入下一环开挖过程计算。如此循环进行,直至隧道开挖完成。

图1 三维数值模型Fig.1 Three dimensional numerical model

图2 盾构隧道开挖循环流程Fig.2 The loop process of shield excavation
2.3 参数赋值
根据地质勘察报告,对物理模型中各计算参数赋值如下。
1)衬砌管片:弹性模量3.7×104MPa,泊松比0.17,密度25kN/m3.
2)注浆体:弹性模量4MPa,泊松比0.31,密度24kN/m3,黏聚力15kPa,内摩擦角25°.
各层土体的物理力学参数如表1所示。
2.4 数值试验方案
盾构隧道开挖过程中,上部水体产生的水头压力对隧道开发有显著影响。数值试验中有序改变水头压力,重点分析湖水深度为5,10,20,30m的4个工况下盾构隧道开挖过程中围岩的变形与渗透规律,以及管片内力分布的变化规律。
工况1:考虑流-固耦合作用并采用有效应力法,湖水深度为5m.
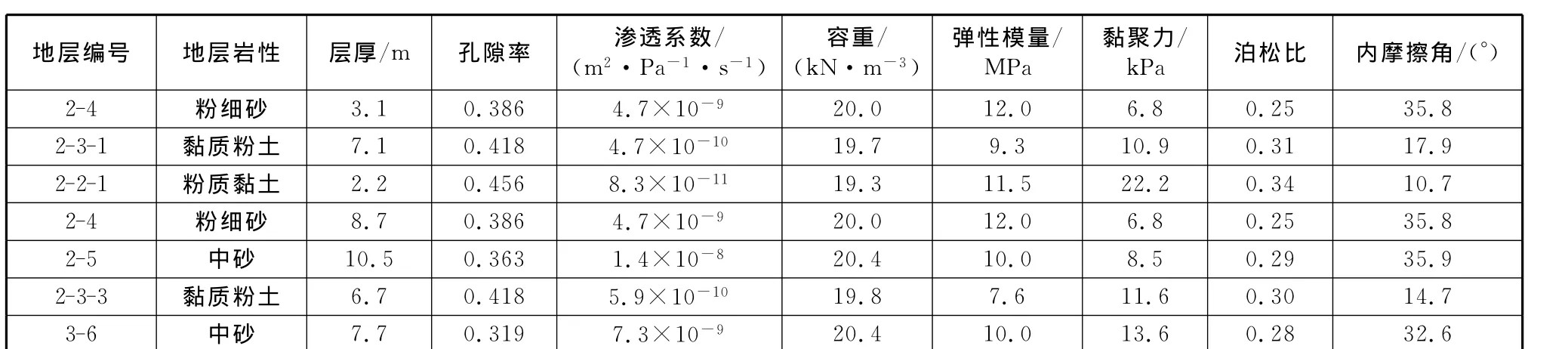
表1 模型计算参数Table 1 Model calculation parameters
工况2:湖水深度为10m,物理模型上表面施加1×105Pa的应力边界和1×105Pa的孔隙压。
工况3:湖水深度为20m,物理模型上表面施加2×105Pa的应力边界和2×105Pa的孔隙压。
工况4:湖水深度为30m,物理模型上表面施加3×105Pa的应力边界和3×105Pa的孔隙压。
3 水下盾构隧道施工扰动下地表沉降及其渗透性分析
3.1 不同水头压力下的地表沉降
盾构隧道施工完毕后,选取隧道坐标Y=78m处断面为研究对象,分析对比不同水压(湖水深度分别为5,10,20,30m)作用下盾构隧道围岩地表沉降量和水平位移,结果如图3、图4所示。

图3 地表竖向沉降曲线Fig.3 Vertical settlement curve of the surface
由图3可见,流-固耦合作用下,4种工况下地表竖向沉降曲线发展趋势基本一致,大体呈“V”形分布,越靠近隧道中心,地表沉降量越大,在两隧道中心线的上方地表沉降值达到最大,且在远离隧道中心点的各地表点也存在较大且均匀的沉降。随着水头压力的增加,地表沉降量和影响范围逐渐增大。
由图4可以看出,4种工况下地表水平位移曲线变化趋势也基本一致,大致呈“双弓形”,水平位移呈现先增大后减小的趋势。在距离隧道中心大约15m处,水平位移达到最大;在距离中心大约40m处,水平位移趋零;同时,地表水平位移量随着水头压力的增加而增大。这主要是因为:随着隧道的开挖,隧道附近孔隙水压力降低,导致水力坡降增大,地下水受动水压力驱动向隧道渗流,土体因发生渗流运动而形成了固结沉降;当水头压力增大时,孔隙水压力也会随之增大,隧道开挖会引起高孔隙水压力的降低,从而形成更大的固结沉降。

图4 地表水平位移曲线图Fig.4 Horizontal surface displacement curve
3.2 不同水头压力下隧道围岩渗流场分布规律
使用后处理软件Tecplot绘制坐标Y=78m处隧道断面在各工况下的孔隙水压力等值线图,如图5所示。
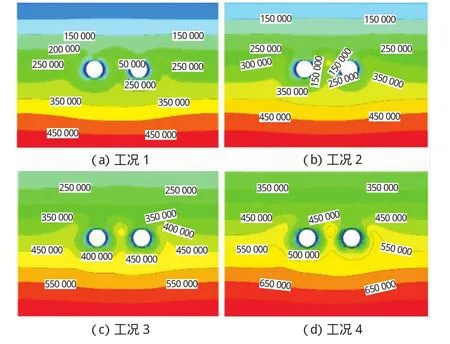
图5 各工况下围岩孔隙水压力等值线图(单位:Pa)Fig.5 Contour map of pore water pressure of surrounding rock under various working conditions
由于隧道施工对土体产生扰动,土体的渗透性发生变化,孔隙水压力降低使得水力坡降增大。在水力坡降的驱动下,远端地下水向隧道方向流动,最终在隧道周围形成类似“降水漏斗状”的孔隙压力分布。隧道周边的水力梯度与水头压力呈正相关,水头压力越大,水力梯度就越大。这一现象在隧道拱腰两侧尤为显著。因此,在施工过程中应当重点监测隧道拱腰两侧水压情况,及时进行壁后注浆,避免形成隧道周边渗流通道。同时,为了保证盾尾处的密实性,应在盾构机尾刷处注入足量的保护油脂,防止盾尾击穿。
对湖水深度与盾构管片周围孔隙水压力进行拟合,得出的拟合曲线如图6所示。

图6 盾构管片周围孔隙水压力与湖水深度关系拟合曲线Fig.6 Fitting curve of relation between pore water pressure and lake water depth around the tunnel
3.3 管片壁后水压力随水头压力的演变规律
盾构隧道施工完成后,在不同工况下,管片后孔隙水压力分布出现明显变化。隧道开挖完成后右线隧道中部管片在4种工况下的孔隙水压力分布如图7所示。

图7 各工况下管片后水压力分布云图Fig.7 Cloud diagram of water pressure distribution after pipe piece under various working conditions
从图7可看到,管片后孔隙水压力随水头压力的增大而增大,其最大值位于管片底部。在最大水头压力(工况4)下管片底部后孔隙水压力约为0.317MPa,比最小水头压力(工况1)下管片底部后孔隙水压力增大了约2倍。
在管片上布置4处孔隙水压力特征点,如图8所示。表2列出了4个特征点在4种工况下的孔隙水压力值。通过比较可以得出:管片壁后孔隙水压力与水头压力呈正比例关系,即水头压力越大,管片后孔隙水压力越大。在相同水头压力下,管片底部孔隙水压力最大,顶部次之,两侧最小。

图8 管片特征点布置图Fig.8 Layout of feature points of pipe fitting

表2 各工况下管片特征点孔隙水压力Table 2 Pore water pressure value of the characteristic point of the pipe in each working condition
3.4 管片内力分析
考虑到各工况下的流-固耦合作用,在两侧隧道开挖完成后,选取左线隧道中部管片为分析对象,得到4种工况下管片的内力分布云图,如图9-图11所示。
由图9可知,管片的弯矩在不同水压作用下的分布规律大致相同。正弯矩主要分布在衬砌管片的拱顶两侧,负弯矩主要分布在衬砌管片的拱底两侧。水头压力越大,正负弯矩的绝对值越大。
由图10可知,尽管作用的水压不同,但是衬砌管片的轴力均为压应力,轴力最大值分布在衬砌管片的拱顶两侧,且水头压力越大,衬砌管片轴力越大。
由图11可知,正剪应力主要分布在衬砌管片的拱顶、拱顶两侧部位及拱底两侧部位,衬砌管片的负剪应力分布随水压的增加逐渐趋于拱腰两侧。

图9 隧道开挖完成后左线中部管片弯矩云图Fig.9 Moment cloud diagram of the middle segment of the left line after tunnel excavation

图10 隧道开挖完成后左线中部管片轴力云图Fig.10 Axial force cloud diagram of the middle segment of the left line after tunnel excavation
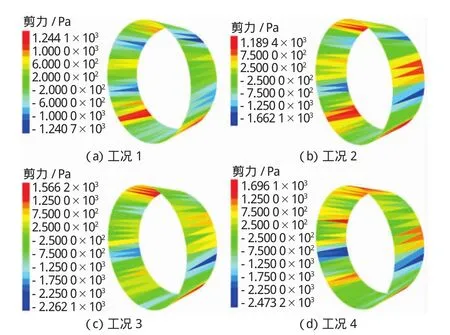
图11 隧道开挖完成后左线中部管片剪力云图Fig.11 Shear force cloud diagram of the middle segment of the left line after tunnel excavation
4 结论
1)流-固耦合作用下,湖底土体竖向沉降量、水平位移量随着湖水深度的增大而增大。湖水深度越大,隧道围岩稳定性越差,发生冒顶、湖水倒灌等事故的可能性就越大。
2)水体下盾构隧道的开挖直接影响着隧道围压孔隙水压力的分布。施工过程中隧道拱顶、拱腰两侧形成较大的水力坡降,上覆湖水深度增大,隧道周围的水力坡降也会随之增大。在工程中应重点监测隧道拱腰两侧孔隙水压力变化,充分做好防排水措施,以防止发生涌水事故。
3)管片壁后孔隙水压力受水头压力的影响显著。水头压力越大,管片后孔隙水压力就越大;相同水头压力下,管片底部孔隙水压力最大,顶部次之,两侧最小。
4)流-固耦合作用下,湖水深度越大,衬砌管片所受的内力就越大,两者呈正相关性。因此,必须根据工程实际情况对盾构管片进行配筋设计。

